Zaawansowane algorytmy i struktury danych/Wykład 3: Różnice pomiędzy wersjami
Nie podano opisu zmian |
|||
| Linia 5: | Linia 5: | ||
W module tym | W module tym zajmiemy się wykrywaniem regularności w tekstach: szukaniem symetrii i powtórzeń. Słowo jest powtórzeniem, gdy jest postaci <math>zz</math>, gdzie <math>z</math> jest niepustym tekstem. Powtórzenia w tekstach reprezentują strukturę wewnętrznych okresowości i regularności, których wyszukiwanie ma zastosowania np. w biologii obliczeniowej. Powtórzenia są związane z kompresją tekstów. Im więcej powtórzeń w słowie, tym bardziej jest kompresowalne. | ||
Słowo jest symetryczne gdy <math>x\ =\ x^R</math>, gdzie <math>^R</math> jest operacją odwracania słowa. Algorytmicznie symetrie w | Słowo jest symetryczne, gdy <math>x\ =\ x^R</math>, gdzie <math>^R</math> jest operacją odwracania słowa. Algorytmicznie symetrie w | ||
słowach są bardzo interesujące. | słowach są bardzo interesujące. | ||
== Kompresja typu LZ i faktoryzacja tekstów == | == Kompresja typu LZ i faktoryzacja tekstów == | ||
Powtarzające się segmenty tekstu związane są z kompresją. Jeśli mamy dwie kopie tego samego (być może długiego) podsłowa, to drugą z nich możemy zastąpić referencją do pierwszej. Jeśli czytamy tekst od lewej do prawej i napotkamy segment <math>x[i..j]</math>, który pojawił się wcześniej jako <math>x[p..q]</math>, gdzie <math>q<i</math> to | Powtarzające się segmenty tekstu związane są z kompresją. Jeśli mamy dwie kopie tego samego (być może długiego) podsłowa, to drugą z nich możemy zastąpić referencją do pierwszej. Jeśli czytamy tekst od lewej do prawej i napotkamy segment <math>x[i..j]</math>, który pojawił się wcześniej jako <math>x[p..q]</math>, gdzie <math>q<i</math>, to możemy reprezentować <math>x[i..j]</math> przez parę liczb <math>[p,q]</math>. Filozofia ta prowadzi do rodziny algorytmów kompresji podanych przez Lempela i Ziva (kompresji typu LZ). Jest wiele różnych wariantów tego typu kompresji. | ||
Zdefiniujmy teraz faktoryzację tekstów typu LZ. Faktoryzacją tekstu <math>x</math> jest rozkład <math>x\ =\ v_{1}v_{2}\dots v_{m}</math>, gdzie <math>v_1=x[1]</math>, oraz <br> | Zdefiniujmy teraz faktoryzację tekstów typu LZ. Faktoryzacją tekstu <math>x</math> jest rozkład <math>x\ =\ v_{1}v_{2}\dots v_{m}</math>, gdzie <math>v_1=x[1]</math>, oraz <br> | ||
| Linia 23: | Linia 24: | ||
Obliczanie następnego czynnika w faktoryzacji typu LZ zaczynającego się na pozycji <math>i</math>-tej (jako najdłuższego | Obliczanie następnego czynnika w faktoryzacji typu LZ zaczynającego się na pozycji <math>i</math>-tej (jako najdłuższego | ||
słowa, które występuje we wcześniejszym tekście). | słowa, które występuje we wcześniejszym tekście). | ||
Poprzedni czynnik kończy się na pozycji <math>i-1</math>. <math>Pos(i)</math> jest początkiem wcześniejszego segmentu | Poprzedni czynnik kończy się na pozycji <math>i-1</math>. <math>Pos(i)</math> jest początkiem wcześniejszego segmentu, | ||
który jest referencją aktualnego czynnika. | który jest referencją aktualnego czynnika. | ||
</center> | </center> | ||
| Linia 36: | Linia 37: | ||
Korzystając z drzew sufiksowych można udowodnić następujący fakt: | Korzystając z drzew sufiksowych można udowodnić następujący fakt: | ||
Dla danego tekstu <math>x</math> długości <math>n</math> możemy policzyć <math>LZ(x)</math> w | |||
czasie liniowym. Zakładamy tutaj, że alfabet da się posortować w czasie liniowym (jest to naturalne | czasie liniowym. Zakładamy tutaj, że alfabet da się posortować w czasie liniowym (jest to naturalne | ||
założenie). | założenie). | ||
| Linia 42: | Linia 43: | ||
== Powtórzenia zakotwiczone == | == Powtórzenia zakotwiczone == | ||
Przypuśćmy, że <math>x=uv</math>. Powtórzenie jest <math>(u,v)</math>-zakotwiczone gdy zaczyna się w <math>u</math> i kończy w <math>v</math>. | Przypuśćmy, że <math>x=uv</math>. Powtórzenie jest <math>(u,v)</math>-zakotwiczone, gdy zaczyna się w <math>u</math> i kończy w <math>v</math>. | ||
Wprowadzimy dwie funkcje logiczne <math>RighTest(u,v), \ LeftTEst(u,v)</math> dla słów <math>u,\ v</math>. <math>RightTest(u,v)</math> | Wprowadzimy dwie funkcje logiczne <math>RighTest(u,v), \ LeftTEst(u,v)</math> dla słów <math>u,\ v</math>. <math>RightTest(u,v)</math> | ||
zachodzi, gdy istnieje <math>(u,v)</math>-zakotwiczone powtórzenie którego środek znajduje się na początku | zachodzi, gdy istnieje <math>(u,v)</math>-zakotwiczone powtórzenie, którego środek znajduje się na początku lub wewnątrz <math>v</math>. Podobnie definiujemy <math>LeftTest</math>. | ||
Rozważmy przypadek obliczania <math>RightTest</math>. | |||
| Linia 55: | Linia 56: | ||
Dla każdej pozycji <math>k</math> w <math>v</math> liczymy | Dla każdej pozycji <math>k</math> w <math>v</math> liczymy | ||
# <math>PREF[k]</math>: długość maksymalnego podsłowa zaczynającego się w <math>k</math> i będącego prefiksem <math>v</math>; | # <math>PREF[k]</math>: długość maksymalnego podsłowa zaczynającego się w <math>k</math> i będącego prefiksem <math>v</math>; | ||
# <math>S[k]</math>: długość maksymalnego podsłowa kończącego | # <math>S[k]</math>: długość maksymalnego podsłowa kończącego się na pozycji <math>k-1</math> i będącego sufiksem <math>u</math>. | ||
'''Własność funkcji''' <math>Righttest</math>:<br> | '''Własność funkcji''' <math>Righttest</math>:<br> | ||
<math>Rightest(u,v)</math> zachodzi wtedy i tylko wtedy gdy dla pewnego <math>k</math> mamy nierówność | <math>Rightest(u,v)</math> zachodzi wtedy i tylko wtedy, gdy dla pewnego <math>k</math> mamy nierówność | ||
<math>PREF[k]+S[k] \geq k</math>, patrz rysunek. | <math>PREF[k]+S[k] \geq k</math>, patrz rysunek. | ||
Wiemy już jak obliczyć tablicę <math>PREF</math> | Wiemy już jak obliczyć tablicę <math>PREF</math> w czasie liniowym, tablicę <math>S</math> liczymy symetrycznie. W ten sposób pokazaliśmy, że obliczenie <math>RightTest(u,v)</math> wymaga jedynie czasu liniowego. Podobnie jest dla <math>LeftTest</math>. | ||
== Szukanie dowolnych powtórzeń w czasie n log n == | == Szukanie dowolnych powtórzeń w czasie n log n == | ||
Niech <math>Test(u,v)</math> będzie funkcją logiczną wyrażającą fakt posiadania przez <math>x</math> | Niech <math>Test(u,v)</math> będzie funkcją logiczną wyrażającą fakt posiadania przez <math>x</math> | ||
powtórzenia <math>(u,v)</math>-zakotwiczonego. Inaczej mówiąc <math>Test(u,v) \equiv RightTest(u,v)\ \textrm{lub}\ Lefttest(u,v)</math>. | powtórzenia <math>(u,v)</math>-zakotwiczonego. Inaczej mówiąc, <math>Test(u,v) \equiv RightTest(u,v)\ \textrm{lub}\ Lefttest(u,v)</math>. | ||
Następujący algorytm ma strukturę taką jak ''merge-sort''. Szukamy powtórzenia w lewej połowie, w prawej | Następujący algorytm ma strukturę taką, jak ''merge-sort''. Szukamy powtórzenia w lewej połowie, w prawej | ||
oraz | oraz na styku obu połówek (funkcja Test). | ||
| Linia 85: | Linia 86: | ||
'''Dygresja.''' | '''Dygresja.''' | ||
Istnieje ciekawa wersja tego algorytmu działająca w czasie <math>O(n \log n)</math> i (dodatkowej) pamięci stałej (nie możemy mieć dodatkowych tablic <math>PREF,\ S</math>). | Istnieje ciekawa wersja tego algorytmu, działająca w czasie <math>O(n \log n)</math> i (dodatkowej) pamięci stałej (nie możemy mieć dodatkowych tablic <math>PREF,\ S</math>). | ||
== Szukanie dowolnych powtórzeń w czasie liniowym == | == Szukanie dowolnych powtórzeń w czasie liniowym == | ||
| Linia 92: | Linia 93: | ||
<center><math>LZ(x)\ =\ (v_{1},v_{2},\dots ,v_{m})</math></center> | <center><math>LZ(x)\ =\ (v_{1},v_{2},\dots ,v_{m})</math></center> | ||
<math>x</math> zawiera powtórzenie wtedy i tylko wtedy, gdy dla pewnego <math>k</math> zachodzi | |||
<math>RightTest(v_1, v_2\ldots v_{k-2},\ v_{k-1}v_k</math> lub <math>Righttest(v_1, v_2\ldots v_{k-1},\ v_k)</math> | <math>RightTest(v_1, v_2\ldots v_{k-2},\ v_{k-1}v_k</math> lub <math>Righttest(v_1, v_2\ldots v_{k-1},\ v_k)</math> | ||
| Linia 113: | Linia 114: | ||
==Wykrywanie symetrii w tekstach == | ==Wykrywanie symetrii w tekstach == | ||
Słowo <math>x</math> nazwiemy palindromem gdy jest symetryczne oraz <math>|x|>1</math>. Palindromy parzyste to palindromy o parzystej długości. Oznaczmy zbiór wszystkich palindromów przez <math>PAL</math>, a przez <math>PAL_0,PAL_1</math> oznaczmy odpowiednio zbiory palindromów parzystych i nieparzystych. | Słowo <math>x</math> nazwiemy palindromem, gdy jest symetryczne oraz <math>|x|>1</math>. Palindromy parzyste to palindromy o parzystej długości. Oznaczmy zbiór wszystkich palindromów przez <math>PAL</math>, a przez <math>PAL_0,PAL_1</math> oznaczmy odpowiednio zbiory palindromów parzystych i nieparzystych. | ||
Przykładami palindromów są słowa: | Przykładami palindromów są słowa: | ||
| Linia 120: | Linia 121: | ||
Problem '''najdłuższego prefikso-palindromu''' polega na rozkładzie danego słowa <math>x =\ uv</math> | Problem '''najdłuższego prefikso-palindromu''' polega na rozkładzie danego słowa <math>x =\ uv</math> takim, że <math>u\in PAL</math> oraz <math>u</math> jest | ||
najdłuższy o tej własności. Istnieje prosty algorytm oparty na tablicy prefikso-sufiksów <math>P</math>. | najdłuższy o tej własności. Istnieje prosty algorytm oparty na tablicy prefikso-sufiksów <math>P</math>. | ||
| Linia 130: | Linia 131: | ||
}} | }} | ||
Podobnie możemy zdefiniować problem najkrótszego prefisko-palindromu. Algorytm powyższy można łatwo zmodyfikować aby znajdował najkrótszy prefikso-palindrom. | Podobnie możemy zdefiniować problem najkrótszego prefisko-palindromu. Algorytm powyższy można łatwo zmodyfikować, aby znajdował najkrótszy prefikso-palindrom. | ||
Chociaż powyższy algorytm działa w czasie liniowym, możliwy jest szybszy algorytm, który znajduje najkrótszy prefikso-palindrom w czasie <math>O(s)</math>, gdzie <math>s</math> jest długością najkrótszego prefikso-palindromu, | Chociaż powyższy algorytm działa w czasie liniowym, możliwy jest szybszy algorytm, który znajduje najkrótszy prefikso-palindrom w czasie <math>O(s)</math>, gdzie <math>s</math> jest długością najkrótszego prefikso-palindromu, założywszy że tekst posiada prefikso-palindrom. | ||
Skoncentrujemy się na razie na palindromach parzystych. | Skoncentrujemy się na razie na palindromach parzystych. | ||
Definiujemy | Definiujemy dla każdej pozycji <math>i</math> ''promień'' palindromu parzystego o środku w <math>i</math> jako: | ||
<center><math>Rad[i]\ =\ \max \{j\ :\ j=0 \ \textrm{lub}\ x[i-j+1.. i]=x[i+1.. i+j]\}</math></center> | <center><math>Rad[i]\ =\ \max \{j\ :\ j=0 \ \textrm{lub}\ x[i-j+1.. i]=x[i+1.. i+j]\}</math></center> | ||
| Linia 141: | Linia 142: | ||
Załóżmy, dla uproszczenia, że tekst <math>x</math> zaczyna się od specjalnego symbolu (marker początku), który występuje tylko na początku. | Załóżmy, dla uproszczenia, że tekst <math>x</math> zaczyna się od specjalnego symbolu (marker początku), który występuje tylko na początku. | ||
Opiszemy algorytm, który oblicza tablice promieni palindromów dla kolejnych pozycji <math>i</math> od strony lewej do prawej, | Opiszemy algorytm, który oblicza tablice promieni palindromów dla kolejnych pozycji <math>i</math> od strony lewej do prawej. Załóżmy, że policzyliśmy już wartości: | ||
<center><math>Rad[1],\, Rad[2],\, \dots ,\, Rad[i].</math></center> | <center><math>Rad[1],\, Rad[2],\, \dots ,\, Rad[i].</math></center> | ||
Okazuje się, że korzystając z symetrii | Okazuje się, że korzystając z symetrii możemy obliczyć pewne nowe elementy tablicy <math>Rad</math>, nie wykonując żadnych porównań symboli. Wynika to z następującego faktu. | ||
| Linia 156: | Linia 157: | ||
'''Przypadek (a):''' <math>Rad[i-k]<Rad[i]-k</math>. | '''Przypadek (a):''' <math>Rad[i-k]<Rad[i]-k</math>. | ||
Wówczas palindrom <math>Rad[i-k]</math> o | Wówczas palindrom <math>Rad[i-k]</math> o środku w <math>i-k</math> jest całowicie zawarty w dłuższym palindromie o środku w <math>i</math>. Pozycja <math>i-k</math> jest symetryczna do <math>i+k</math> ze względu na <math>i</math>. Zatem z symetrii o środku <math>i</math> wynika, że najdłuższy palindrom o środku <math>i+k</math> ma taki sam promień jak ten o środku <math>i-k</math>. Zatem w tym przypadku <math>Rad[i+k]=Rad[i-k]</math>. | ||
'''Przypadek (b):''' <math>Rad[i-k]>Rad[i]-k</math>. | '''Przypadek (b):''' <math>Rad[i-k]>Rad[i]-k</math>. | ||
Sytuacja jest pokazna na rysunku, który przedstawia maksymalne palindromy o środkach <math>i-k</math>, <math>i</math> | Sytuacja jest pokazna na rysunku, który przedstawia maksymalne palindromy o środkach <math>i-k</math>, <math>i</math> i <math>i+k</math>. | ||
Ponieważ <math>a\ne b</math> (z definicji maksymalności palindromu o środku w <math>i</math>), zatem <math>Rad[i+k]=Rad[i]-k</math>. | Ponieważ <math>a\ne b</math> (z definicji maksymalności palindromu o środku w <math>i</math>), zatem <math>Rad[i+k]=Rad[i]-k</math>. | ||
| Linia 166: | Linia 167: | ||
Przypadek (b) dowodu własności promieni palindromów parzystych.</center> | Przypadek (b) dowodu własności promieni palindromów parzystych.</center> | ||
Poniżej przedstawiamy algorytm Promienie-Palindromów. W jednej głównej iteracji pętli | Poniżej przedstawiamy algorytm Promienie-Palindromów. W jednej głównej iteracji pętli while algorytm oblicza <math>Rad[i+k]</math> dla kolejnych <math>k=1,2,\dots </math>, dla których <math>Rad[i-k]\neq Rad[i]-k</math>. Jeśli ostatnim takim <math>k</math> jest <math>k'</math>, | ||
wtedy zaczynamy całą główną iterację | wtedy zaczynamy całą główną iterację od nowego <math>i</math> równego <math>i+k'</math>. | ||
Pozostawiamy jako ćwiczenie modyfikację algorytmu aby liczył promienie palindromów nieparzystych. | Pozostawiamy jako ćwiczenie modyfikację algorytmu, aby liczył promienie palindromów nieparzystych. | ||
W | W pierwszym momencie, gdy algorytm wykryje prefikso-palindrom (promień palindromu sięga do początku tekstu), możemy algorytm zatrzymać i podać długość najkrótszego prefikso-palindromu. W sumie pokazaliśmy następujący fakt: | ||
'''(a) ''' Tablicę promieni palindromów (parzystych i nieparzystych) można policzyć w czasie liniowym. | '''(a) ''' Tablicę promieni palindromów (parzystych i nieparzystych) można policzyć w czasie liniowym. | ||
| Linia 199: | Linia 200: | ||
Elementy <math>PAL^*</math> nazywamy ''palstarami'' a elementy <math>PAL_0^*</math> nazywamy ''palstarami parzystymi''. | Elementy <math>PAL^*</math> nazywamy ''palstarami'' a elementy <math>PAL_0^*</math> nazywamy ''palstarami parzystymi''. | ||
Niech <math>first(i)</math>, <math>first_0(i)</math> będzie (ze względów technicznych załóżmy, że słowo puste | Niech <math>first(i)</math>, <math>first_0(i)</math> będzie (ze względów technicznych załóżmy, że słowo puste też jest palstarem (parzystm i nieparzystym jednocześnie)) odpowiednio pierwszą pozycją <math>j>i</math> w słowie <math>x</math> taką, że <math>x[i.. j]\in PAL</math>, <math>x[i.. j]\in PAL_0</math>, wartością funkcji zaś jest zero, gdy nie ma takiego <math>j</math>. | ||
| Linia 212: | Linia 213: | ||
Mówiąc nieformalnie, algorytm Parzyste-Palstary obcina słowo o najkrótszy prefikso-palindrom, aż tekst będzie pusty (sukces) albo aż się ''em zatnie'' (nie ma rozkładu na parzyste palindromy). Algorytm Parzyste-Palstary ma złożoność liniową ponieważ policzenie <math>first_0(i)</math> zajmuje czas proporcjonalny do wartości <math>s=first(i)</math>, zakładając, że <math>s \ne 0</math>. Nietrywialna natomiast jest poprawność algorytmu. Zdefiniujmy | Mówiąc nieformalnie, algorytm Parzyste-Palstary obcina słowo o najkrótszy prefikso-palindrom, aż tekst będzie pusty (sukces) albo aż się ''em zatnie'' (nie ma rozkładu na parzyste palindromy). Algorytm Parzyste-Palstary ma złożoność liniową, ponieważ policzenie <math>first_0(i)</math> zajmuje czas proporcjonalny do wartości <math>s=first(i)</math>, zakładając, że <math>s \ne 0</math>. Nietrywialna natomiast jest poprawność algorytmu. Zdefiniujmy | ||
<center> <math>parse_0(i)=\min \{j\ :\ x[i.. j]\in PAL_0</math> oraz <math>j=n</math> lub <math>x[j+1.. n]\in PAL_0^{*}\}</math></center> | <center> <math>parse_0(i)=\min \{j\ :\ x[i.. j]\in PAL_0</math> oraz <math>j=n</math> lub <math>x[j+1.. n]\in PAL_0^{*}\}</math></center> | ||
| Linia 219: | Linia 220: | ||
'''Własność parzystych palstarów:''' <math>x[i..n] \in PAL_0^* \ \Rightarrow\ parse_0(i)=first_0(i)</math> | '''Własność parzystych palstarów:''' <math>x[i..n] \in PAL_0^* \ \Rightarrow\ parse_0(i)=first_0(i)</math> | ||
Poprawność algorytmu wynika natychmiast | Poprawność algorytmu wynika natychmiast z powyższej własności. Pozostawiamy dowód tej własności jako ćwiczenie. | ||
Możemy podobnie zdefiniować funkcję <math>parse(i)</math> dla dowolnych palstarów i dowolnych palindromów. Własność parzystych palstarów nie zachodzi dla dowolnych palstarów, ale zachodzi własność bardziej skomplikowana. | Możemy podobnie zdefiniować funkcję <math>parse(i)</math> dla dowolnych palstarów i dowolnych palindromów. Własność parzystych palstarów nie zachodzi dla dowolnych palstarów, ale zachodzi własność bardziej skomplikowana. | ||
| Linia 227: | Linia 228: | ||
Pozostawimay dowód tej własności | Pozostawimay dowód tej własności jako ćwiczenie. Algorytm testowania dowolnych palstarów jest interesujący, ponieważ przebiega on zupełnie inaczej niż dla parzystych palstarów. | ||
Pierwszym krokiem algorytmu jest stablicowanie funkcji <math>first</math> | Pierwszym krokiem algorytmu jest stablicowanie funkcji <math>first</math>. Obliczamy tablicę <math>FIRST[i]=first(i)</math> w czasie | ||
liniowym dla wszystkich <math>i</math> łącznie. | liniowym dla wszystkich <math>i</math> łącznie. | ||
Pozostawiamy jako ćwiczenie policzenie tej tablicy w czasie <math>O(n)</math>. Obliczenie takie opiera się na wykorzystaniu tablicy promieni palindromów. | Pozostawiamy jako ćwiczenie policzenie tej tablicy w czasie <math>O(n)</math>. Obliczenie takie opiera się na wykorzystaniu tablicy promieni palindromów. | ||
Załóżmy teraz że mamy tablicę FIRST | Załóżmy teraz, że mamy tablicę FIRST. Funkcja <math>first</math> działa teraz w czasie stałym (gotowe wartości z tablicy). Poniższy algorytm | ||
dla każdej pozycji <math>i</math> sprawdza czy <math>x[i..n]\in PAL^*</math>. Odpowiedź jest zapisana w tablicy logicznej <math>PAL</math>. | dla każdej pozycji <math>i</math> sprawdza, czy <math>x[i..n]\in PAL^*</math>. Odpowiedź jest zapisana w tablicy logicznej <math>PAL</math>. | ||
Zakładamy, że początkowo tablica <math>PAL</math> ma wartości {\em false} włącznie z elementami wykraczającymi poza zakres tablicy (dla uproszczenia zapisu). | Zakładamy, że początkowo tablica <math>PAL</math> ma wartości {\em false}, włącznie z elementami wykraczającymi poza zakres tablicy (dla uproszczenia zapisu). | ||
Wersja z 13:21, 25 wrz 2006
Zaawansowane algorytmy tekstowe III
W module tym zajmiemy się wykrywaniem regularności w tekstach: szukaniem symetrii i powtórzeń. Słowo jest powtórzeniem, gdy jest postaci , gdzie jest niepustym tekstem. Powtórzenia w tekstach reprezentują strukturę wewnętrznych okresowości i regularności, których wyszukiwanie ma zastosowania np. w biologii obliczeniowej. Powtórzenia są związane z kompresją tekstów. Im więcej powtórzeń w słowie, tym bardziej jest kompresowalne.
Słowo jest symetryczne, gdy , gdzie jest operacją odwracania słowa. Algorytmicznie symetrie w słowach są bardzo interesujące.
Kompresja typu LZ i faktoryzacja tekstów
Powtarzające się segmenty tekstu związane są z kompresją. Jeśli mamy dwie kopie tego samego (być może długiego) podsłowa, to drugą z nich możemy zastąpić referencją do pierwszej. Jeśli czytamy tekst od lewej do prawej i napotkamy segment , który pojawił się wcześniej jako , gdzie , to możemy reprezentować przez parę liczb . Filozofia ta prowadzi do rodziny algorytmów kompresji podanych przez Lempela i Ziva (kompresji typu LZ). Jest wiele różnych wariantów tego typu kompresji.
Zdefiniujmy teraz faktoryzację tekstów typu LZ. Faktoryzacją tekstu jest rozkład , gdzie , oraz
jeśli , to jest najdłuższym tekstem, który występuje w , a jeśli
takiego nie ma, to .
Oznaczmy przez faktoryzację .
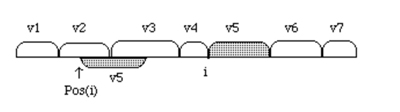
Rysunek 1:
Obliczanie następnego czynnika w faktoryzacji typu LZ zaczynającego się na pozycji -tej (jako najdłuższego słowa, które występuje we wcześniejszym tekście). Poprzedni czynnik kończy się na pozycji . jest początkiem wcześniejszego segmentu, który jest referencją aktualnego czynnika.
Przykład
Faktoryzacja przykładowego słowa Fibonacciego jest następująca:
Korzystając z drzew sufiksowych można udowodnić następujący fakt:
Dla danego tekstu długości możemy policzyć w czasie liniowym. Zakładamy tutaj, że alfabet da się posortować w czasie liniowym (jest to naturalne założenie).
Powtórzenia zakotwiczone
Przypuśćmy, że . Powtórzenie jest -zakotwiczone, gdy zaczyna się w i kończy w . Wprowadzimy dwie funkcje logiczne dla słów . zachodzi, gdy istnieje -zakotwiczone powtórzenie, którego środek znajduje się na początku lub wewnątrz . Podobnie definiujemy .
Rozważmy przypadek obliczania .
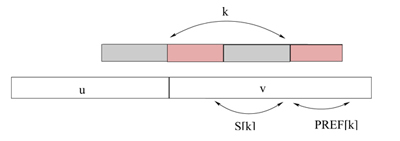
Rysunek 2:
Dla każdej pozycji w liczymy
- : długość maksymalnego podsłowa zaczynającego się w i będącego prefiksem ;
- : długość maksymalnego podsłowa kończącego się na pozycji i będącego sufiksem .
Własność funkcji :
zachodzi wtedy i tylko wtedy, gdy dla pewnego mamy nierówność
, patrz rysunek.
Wiemy już jak obliczyć tablicę w czasie liniowym, tablicę liczymy symetrycznie. W ten sposób pokazaliśmy, że obliczenie wymaga jedynie czasu liniowego. Podobnie jest dla .
Szukanie dowolnych powtórzeń w czasie n log n
Niech będzie funkcją logiczną wyrażającą fakt posiadania przez powtórzenia -zakotwiczonego. Inaczej mówiąc, . Następujący algorytm ma strukturę taką, jak merge-sort. Szukamy powtórzenia w lewej połowie, w prawej oraz na styku obu połówek (funkcja Test).
Algorytm Powtórzenia - Rekurencyjne
if then return false
zastosuj algorytm rekurencyjnie do tekstu ;
zastosuj algorytm rekurencyjnie do tekstu ;
if then return true;
Algorytm w oczywisty sposób działa w czasie , gdyż liczenie funkcji jest w czasie liniowym.
Dygresja.
Istnieje ciekawa wersja tego algorytmu, działająca w czasie i (dodatkowej) pamięci stałej (nie możemy mieć dodatkowych tablic ).
Szukanie dowolnych powtórzeń w czasie liniowym
Algorytm liniowy szukania powtórzenia opiera się na faktoryzacji tekstów. Niech
zawiera powtórzenie wtedy i tylko wtedy, gdy dla pewnego zachodzi
lub
Dowód tej własności pozostawiamy jako ćwiczenie.
Algorytm Szukanie-Powtórzeń
oblicz faktoryzację ;
for to do
;
;
if lub
then return true;
return false;
Algorytm działa w czasie liniowym, pozostawiamy to jako ćwiczenie.
Wykrywanie symetrii w tekstach
Słowo nazwiemy palindromem, gdy jest symetryczne oraz . Palindromy parzyste to palindromy o parzystej długości. Oznaczmy zbiór wszystkich palindromów przez , a przez oznaczmy odpowiednio zbiory palindromów parzystych i nieparzystych.
Przykładami palindromów są słowa:
Problem najdłuższego prefikso-palindromu polega na rozkładzie danego słowa takim, że oraz jest
najdłuższy o tej własności. Istnieje prosty algorytm oparty na tablicy prefikso-sufiksów .
Algorytm Prefikso-Palindrom
- oblicz tablicę P dla słowa-kompozycji (słowo długości ),
- jeśli to jest to długość najdłuższego prefikso-palindromu
- w przeciwnym przypadku nie ma prefikso-palindromu.
Podobnie możemy zdefiniować problem najkrótszego prefisko-palindromu. Algorytm powyższy można łatwo zmodyfikować, aby znajdował najkrótszy prefikso-palindrom.
Chociaż powyższy algorytm działa w czasie liniowym, możliwy jest szybszy algorytm, który znajduje najkrótszy prefikso-palindrom w czasie , gdzie jest długością najkrótszego prefikso-palindromu, założywszy że tekst posiada prefikso-palindrom.
Skoncentrujemy się na razie na palindromach parzystych. Definiujemy dla każdej pozycji promień palindromu parzystego o środku w jako:
Załóżmy, dla uproszczenia, że tekst zaczyna się od specjalnego symbolu (marker początku), który występuje tylko na początku.
Opiszemy algorytm, który oblicza tablice promieni palindromów dla kolejnych pozycji od strony lewej do prawej. Załóżmy, że policzyliśmy już wartości:
Okazuje się, że korzystając z symetrii możemy obliczyć pewne nowe elementy tablicy , nie wykonując żadnych porównań symboli. Wynika to z następującego faktu.
Własność promieni palindromów
Uzasadnimy krótko tę własność rozważając dwa przypadki:
Przypadek (a): .
Wówczas palindrom o środku w jest całowicie zawarty w dłuższym palindromie o środku w . Pozycja jest symetryczna do ze względu na . Zatem z symetrii o środku wynika, że najdłuższy palindrom o środku ma taki sam promień jak ten o środku . Zatem w tym przypadku .
Przypadek (b): .
Sytuacja jest pokazna na rysunku, który przedstawia maksymalne palindromy o środkach , i . Ponieważ (z definicji maksymalności palindromu o środku w ), zatem .

Rysunek 3: Przypadek (b) dowodu własności promieni palindromów parzystych.
Poniżej przedstawiamy algorytm Promienie-Palindromów. W jednej głównej iteracji pętli while algorytm oblicza dla kolejnych , dla których . Jeśli ostatnim takim jest , wtedy zaczynamy całą główną iterację od nowego równego .
Pozostawiamy jako ćwiczenie modyfikację algorytmu, aby liczył promienie palindromów nieparzystych.
W pierwszym momencie, gdy algorytm wykryje prefikso-palindrom (promień palindromu sięga do początku tekstu), możemy algorytm zatrzymać i podać długość najkrótszego prefikso-palindromu. W sumie pokazaliśmy następujący fakt:
(a) Tablicę promieni palindromów (parzystych i nieparzystych) można policzyć w czasie liniowym.
(b) Długość najkrótszego prefikso-palindromu (zakładając że taki istnieje) można policzyć w czasie proporcjonalnym do jego długości.
Algorytm Promienie-Palindromów
; ;
;
while do
while do ;
if then ;
;
while do
; ;
;;
Kompozycje słów symetrycznych
Rozważmy teraz interesujący (chociaż mało użyteczny w praktyce) problem sprawdzania, czy słowo jest nietrywialną kompozycją słów symetrycznych. Przez oznaczmy odpowiednio zbiór konkatenacji dowolnej liczby słów należących do .
Elementy nazywamy palstarami a elementy nazywamy palstarami parzystymi.
Niech , będzie (ze względów technicznych załóżmy, że słowo puste też jest palstarem (parzystm i nieparzystym jednocześnie)) odpowiednio pierwszą pozycją w słowie taką, że , , wartością funkcji zaś jest zero, gdy nie ma takiego .
Algorytm Parzyste-Palstary
;
while do
;
if then return false;
;
return true;
Mówiąc nieformalnie, algorytm Parzyste-Palstary obcina słowo o najkrótszy prefikso-palindrom, aż tekst będzie pusty (sukces) albo aż się em zatnie (nie ma rozkładu na parzyste palindromy). Algorytm Parzyste-Palstary ma złożoność liniową, ponieważ policzenie zajmuje czas proporcjonalny do wartości , zakładając, że . Nietrywialna natomiast jest poprawność algorytmu. Zdefiniujmy
Własność parzystych palstarów:
Poprawność algorytmu wynika natychmiast z powyższej własności. Pozostawiamy dowód tej własności jako ćwiczenie.
Możemy podobnie zdefiniować funkcję dla dowolnych palstarów i dowolnych palindromów. Własność parzystych palstarów nie zachodzi dla dowolnych palstarów, ale zachodzi własność bardziej skomplikowana.
Własność dowolnych palstarów:
Pozostawimay dowód tej własności jako ćwiczenie. Algorytm testowania dowolnych palstarów jest interesujący, ponieważ przebiega on zupełnie inaczej niż dla parzystych palstarów.
Pierwszym krokiem algorytmu jest stablicowanie funkcji . Obliczamy tablicę w czasie liniowym dla wszystkich łącznie.
Pozostawiamy jako ćwiczenie policzenie tej tablicy w czasie . Obliczenie takie opiera się na wykorzystaniu tablicy promieni palindromów.
Załóżmy teraz, że mamy tablicę FIRST. Funkcja działa teraz w czasie stałym (gotowe wartości z tablicy). Poniższy algorytm dla każdej pozycji sprawdza, czy . Odpowiedź jest zapisana w tablicy logicznej . Zakładamy, że początkowo tablica ma wartości {\em false}, włącznie z elementami wykraczającymi poza zakres tablicy (dla uproszczenia zapisu).
Algorytm Testowanie-Palstarów
true;
for down to do
;
if then false
else or or
Interesującym problemem jest rozkład słowa w postaci , gdzie jest ustalone. Istnieją algorytmy liniowe dla oparte na następującej własności zawężającej zbiór rozkładów do zweryfikowania:
jeśli to , dla pewnych gdzie jest najdłuższym palindromem będącym prefiksem lub jest najdłuższym palindromem będącym sufiksem .