MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 322: | Linia 322: | ||
np. ciągu danego wzorem | np. ciągu danego wzorem | ||
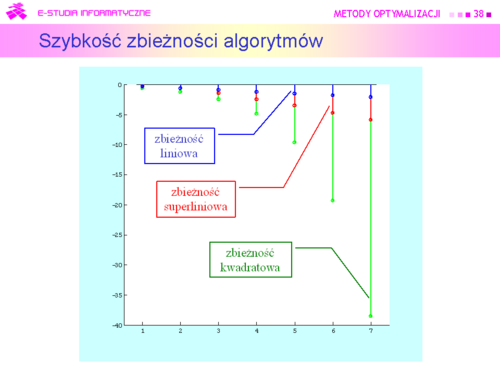
<math>h^{(k)}=k^{-k},k\in 1 \infty (\frac{k^{-(k+1)}}{k^k}=\frac{1}{k}\rightarrow 0)</math> | <math>h^{(k)}=k^{-k},k\in 1 \infty (\frac{k^{-(k+1)}}{k^k}=\frac{1}{k}\rightarrow 0) – zbieżność superliniowa,</math> | ||
np. ciągu danego wzorem | |||
<math>h^{(k)}=2^{-k},k\in 1 \infty (\frac{2^{-2^{k+1}}}{(2^{-2^k})^2}\rightarrow 0)– zbieżność kwadratowa.</math> | |||
|} | |} | ||
| Linia 329: | Linia 333: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd38.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd38.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Na rysunku przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów. | ||
Widać że zbieżność liniowa jest najwolniejsza, a kwadratowa najszybsza. Różne eksperymenty pokazały, że w zastosowaniach praktycznych szybkość liniowa jest do zaakceptowania gdy granica <math>\rho </math> jest dostatecznie mała, nie większa niż <math>\frac{1}{4}</math>. | |||
|} | |} | ||
---- | ---- | ||
| Linia 341: | Linia 347: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd40.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd40.png|thumb|500px]] | ||
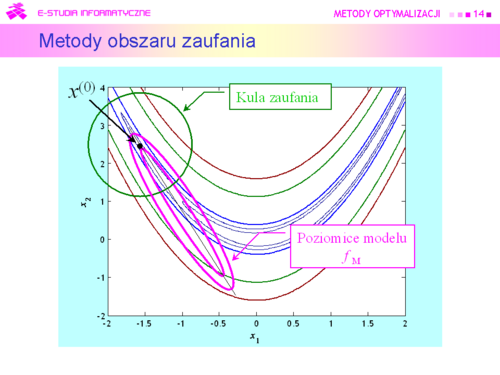
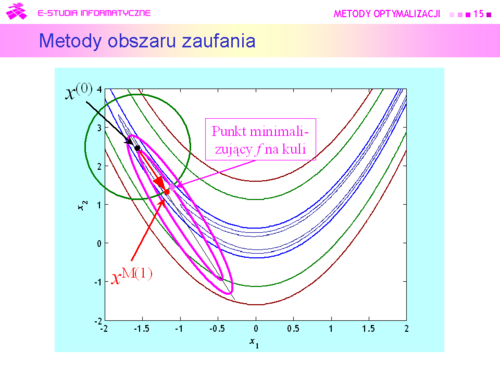
|valign="top"| | |valign="top"|Pierwszy sposób został omówiony dokładnie w wykładzie poprzednim. Została pokazana ograniczoność możliwości jego stosowania. Ogólna zasada działania pozostałych trzech schematów jest taka sama i polega na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę (np. minimalizującego odpowiednio dobraną funkcję). W metodzie obszarów zaufania to zadanie poprawy jest wielowymiarową minimalizacją przy ograniczeniach, najczęściej funkcji kwadratowej. Dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej. Schematy te zostały przedstawione ogólnie i dla zastosowań praktycznych wymagają „doprecyzowania”. Zostanie to uczynione w następnych wykładach. | ||
|} | |} | ||
---- | ---- | ||
Wersja z 13:17, 25 wrz 2006
 |
 |
 |
 |
 |
Algorytm może być:
• ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) –przyjąć xM(k) za środek nowego otoczenia
|
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
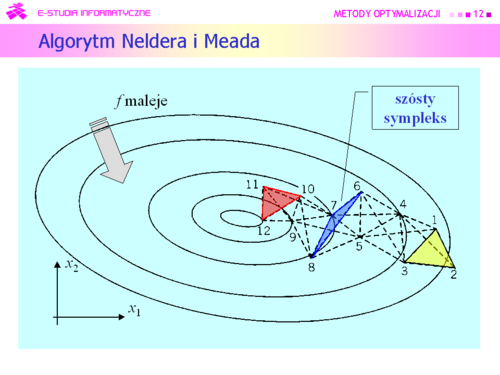 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
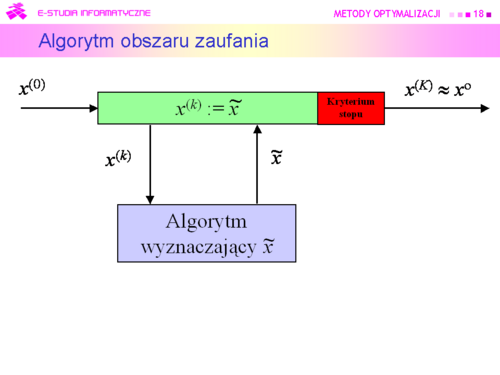
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
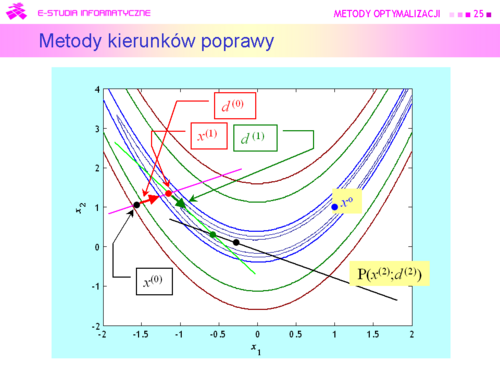
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
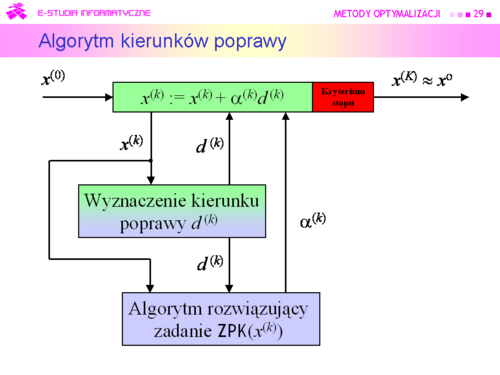
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. |
 |
 |
 |
 |
 |
 |