MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 305: | Linia 305: | ||
a) liniowo, gdy dodatkowo | a) liniowo, gdy dodatkowo | ||
<math>\frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k \rightarrow\infty}\rho\>0</math> | <math>\frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k \rightarrow\infty} \rho\>0</math> | ||
b) superliniowo, gdy dodatkowo | |||
<math>\frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k \rightarrow\infty} 0</math> | |||
c) kwadratowo, gdy dodatkowo | |||
<math>\frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k \rightarrow\infty} \rho \gg 0</math> | |||
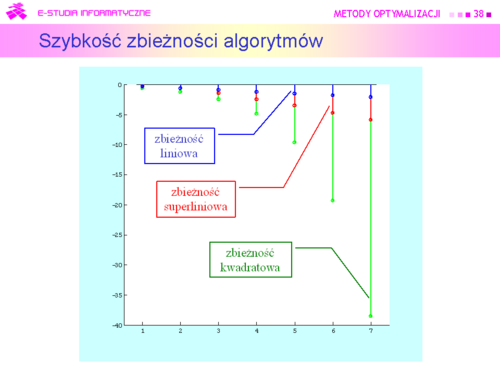
Definicje szybkości związane są z szybkością zbiegania do zera: | |||
postępu geometrycznego o dodatnim ilorazie mniejszym niż jeden, np. danego wzorem | |||
<math>h^{(k)}=2^{-k} (\frac{2^{-(k+1)}}{2^{-k}}=\frac{1}{2}\ge 0) – zbieżność liniowa,</math> | |||
np. ciągu danego wzorem | |||
<math>h^{(k)}=k^{-k},k\in 1 \infty (\frac{k^{-(k+1)}}{k^k}=\frac{1}{k}\rightarrow 0)</math> | |||
|} | |} | ||
Wersja z 13:04, 25 wrz 2006
 |
 |
 |
 |
 |
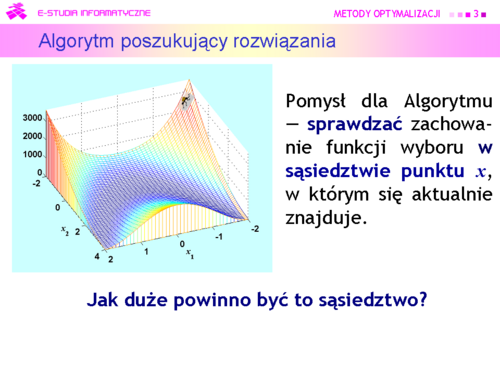
Algorytm może być:
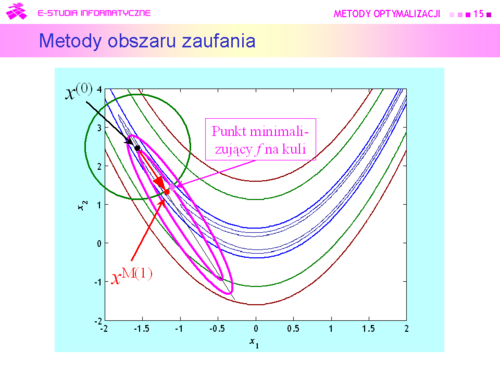
• ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) –przyjąć xM(k) za środek nowego otoczenia
|
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
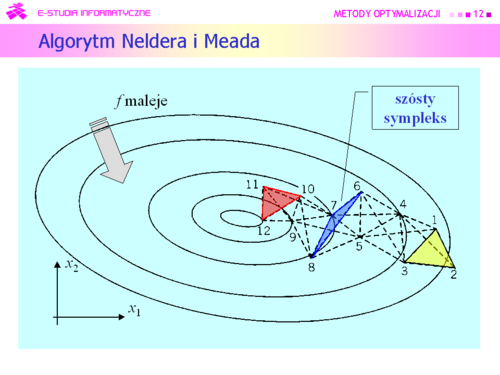 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
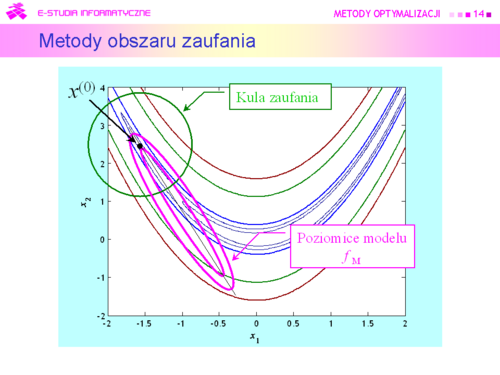
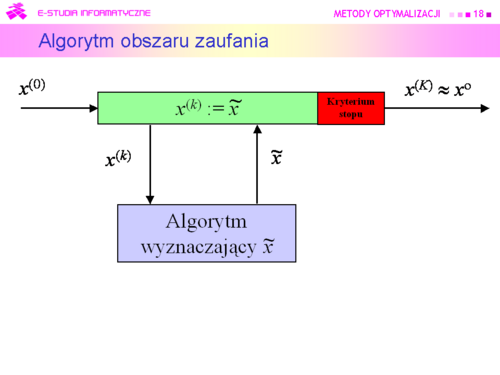
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
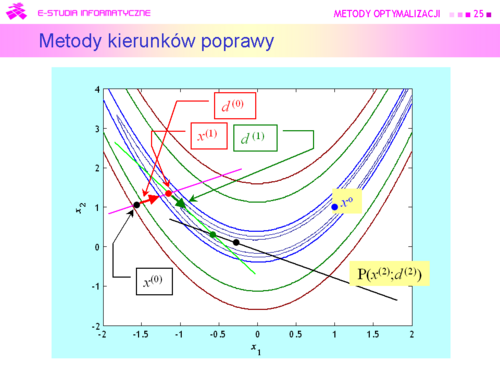
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
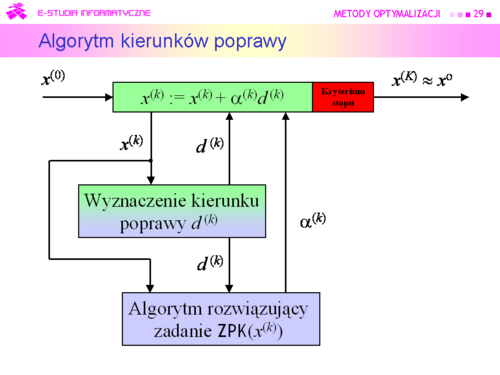
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. |
 |
 |
 |
 |
 |
 |
 |
 |