MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 207: | Linia 207: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | ||
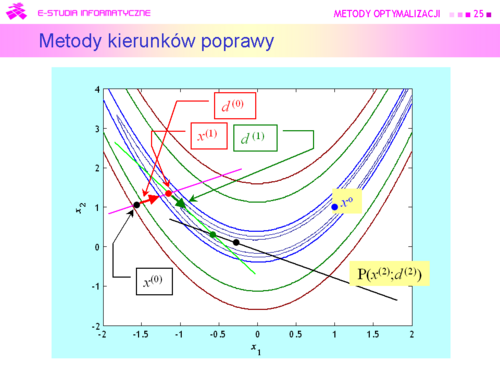
|valign="top"| | |valign="top"|Dokonujemy, jak mówimy minimalizacji w kierunku. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha (x^{(k)}</math> i d są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x(^{k)};d)</math> jest określony jednym ograniczeniem równościowym. | ||
Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | |||
|} | |} | ||
---- | ---- | ||
| Linia 225: | Linia 227: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd29.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd29.png|thumb|500px]] | ||
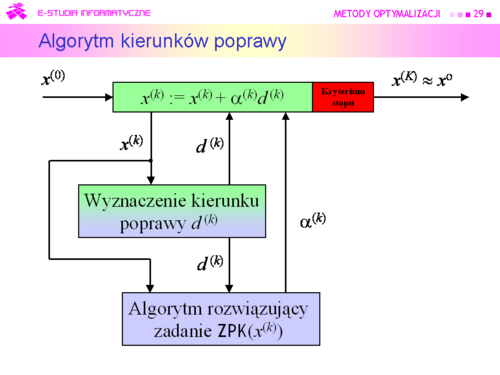
|valign="top"| | |valign="top"|Bardziej formalnie przedstawioną procedurę minimalizacji opartą na generowaniu kierunków poprawy opisuje następujący podstawowy algorytm kierunków poprawy. | ||
Podstawowy algorytm kierunków poprawy | |||
Inicjalizacja | |||
Wybierz punkt początkowy <math>x^{(0)}</math>. | |||
Podstaw k := 0. | |||
Kroki algorytmu | |||
#Dla punktu <math>x^{(k)}</math> wyznacz kierunek poprawy <math>d^{(k)}</math>. | |||
#Ustal długość kroku w kierunku poprawy <math>\alpha ^{(k)}</math>.. | |||
#Wylicz następny punkt podstawiając <math>x^{(k)}:=x^{(k)}+\alpha ^{(k)}d^{(k)}</math>. | |||
#Jeżeli spełnione jest kryterium (test) stopu, to <math>x^{(k)}</math> przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 5. | |||
#Podstaw k := k + 1, idź do 1. | |||
|} | |} | ||
---- | ---- | ||
| Linia 231: | Linia 247: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd30.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd30.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. | ||
|} | |} | ||
---- | ---- | ||
| Linia 243: | Linia 259: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd32.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd32.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Szukanie punktu dającego poprawę: | ||
*w metodzie rozsiewania punktów próbnych jest to zadanie wyboru punktu najmniejszego ze skończonej ich liczby; | |||
*w metodzie obszarów zaufania jest to zadanie wielo-wymiarowej minimalizacji przy ograniczeniach, najczęściej funkcji kwadratowej, zadanie ZKK; | |||
*dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej, zadanie ZPK. | |||
|} | |} | ||
---- | ---- | ||
| Linia 256: | Linia 276: | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
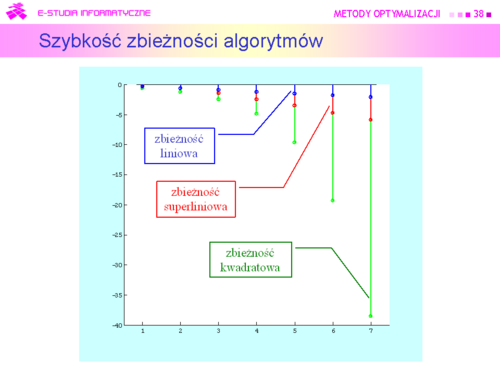
*Zbieżność skończona, która ma miejsce wtedy gdy istnieje taka liczba K dla której x(K) = xo. Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm Simplex rozwiązywania zadań liniowych. Jednak jak pamiętamy, liczba iteracji może być bardzo duża, co oznacza, że na rozwiązanie zadania trzeba bardzo długo czekać. Metody punktu wewnętrznego nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod tego typu. A wniosek ogólny – z praktycznego punktu widzenia zbieżność skończona z bardzo dużym K może być gorsza niż zbieżność nieskończona, w sytuacji w której ciąg szybko zmierza do niewielkiego otoczenia rozwiązania. | |||
Znana Państwu z analizy matematycznej zbieżność wektorowego ciągu nieskończonego, zwana jest w teorii metod optymalizacji krótko zbieżnością (nieskończoną). Jest ona rozumiana dwojako: jako zbieżność do rozwiązania xo, albo dla funkcji gładkich – zbieżność do punktu stacjonarnego gradientu, tzn. takiego wektora , że | |||
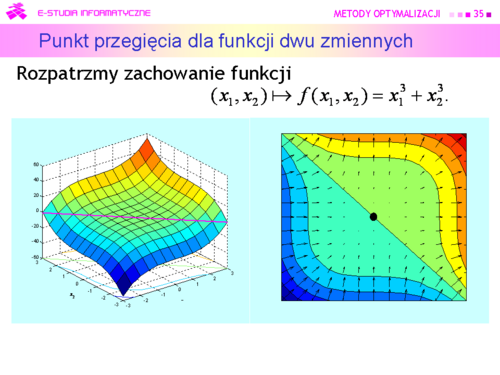
Jak pamiętamy punkt może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie. | |||
Dlatego w niektórych wypadkach twórcom algorytmów udaje się udowodnić własność jeszcze słabszą: ciąg wektorów generowany przez algorytm zawiera podciąg zbieżny. | |||
Akceptacja zbieżności ostatniego rodzaju po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym “optymistycznym” podejściu do analizy sytuacji. | |||
|} | |} | ||
---- | ---- | ||
Wersja z 12:50, 25 wrz 2006
 |
 |
 |
 |
 |
Algorytm może być:
• ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) –przyjąć xM(k) za środek nowego otoczenia
|
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
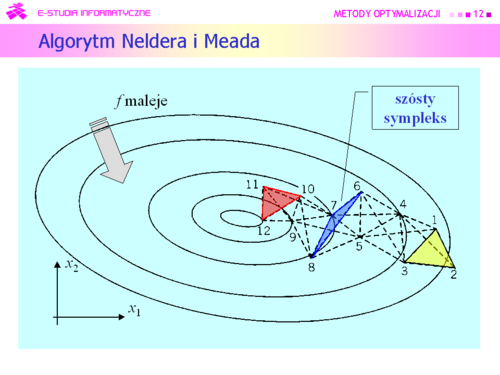 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
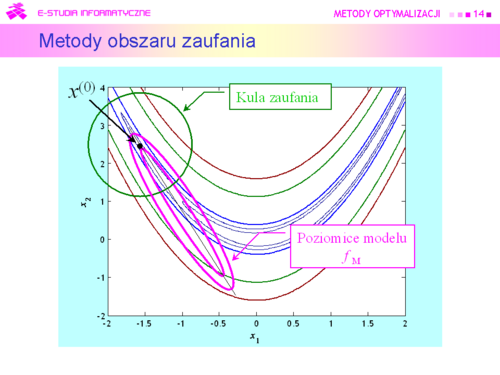
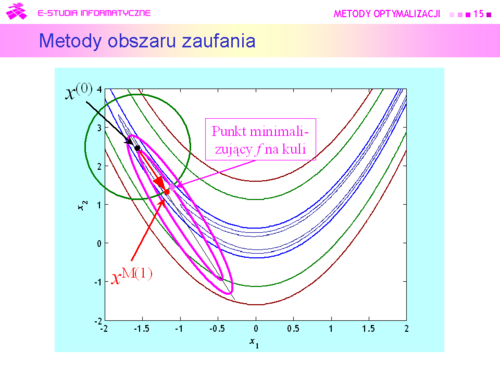
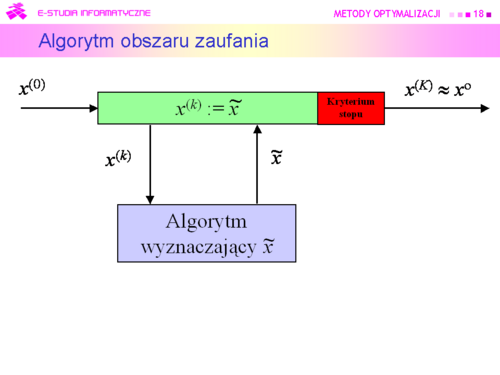
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |