MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 13: | Linia 13: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd3.png|thumb|500px]] | ||
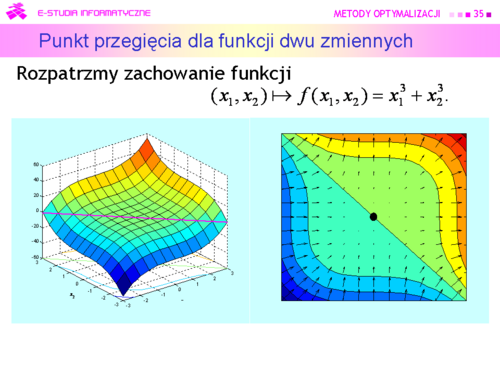
|valign="top"| | |valign="top"|Powróćmy do naszych rozważań z części drugiej wykładu trzeciego. | ||
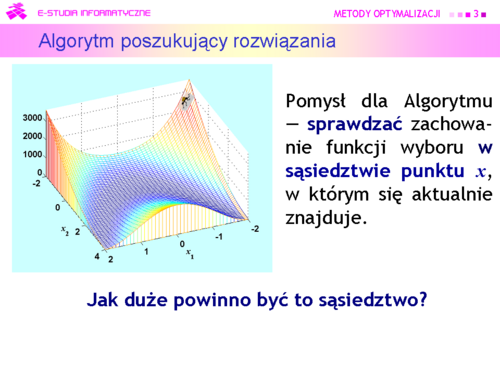
Jak pamiętamy, Algorytm jest ślepy — nie może zobaczyć rzeźby trenu na którym się znajduje. | |||
Na schodach szedł w prawo, potem w lewo — sprawdzał swoje otoczenie. Teraz otoczenie ma więcej wymiarów, ale pomysł może być ten sam — sprawdzać zachowanie funkcji wyboru w sąsiedztwie punktu x, w którym się aktualnie znajduje. | |||
Natychmiast pojawia się pytanie — jak duże powinno być to sąsiedztwo? | |||
Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej). | |||
|} | |} | ||
---- | ---- | ||
| Linia 31: | Linia 36: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd6.png|thumb|500px]] | ||
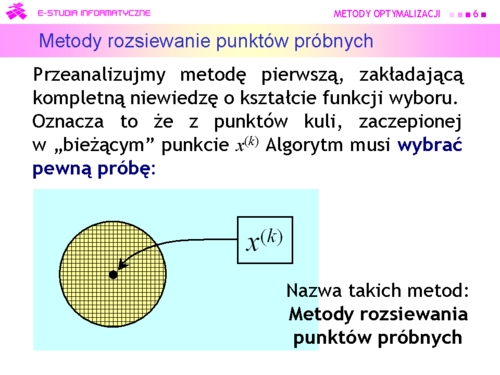
|valign="top"| | |valign="top"|Przeanalizujmy teraz sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów kuli, zaczepionej w „bieżącym” punkcie x(k) Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne). | ||
|} | |} | ||
---- | ---- | ||
| Linia 37: | Linia 42: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Algorytm może być: | ||
• ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) | |||
–przyjąć xM(k) za środek nowego otoczenia | |||
<math>x^{(k+1)}=x^{M(k)}=\alpha (x^{M(k)}-x^(k))+x^{(k)}, \alpha=1</math> | |||
i przeszukiwać je tak jak poprzednio. | |||
|} | |} | ||
---- | ---- | ||
| Linia 43: | Linia 55: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd8.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Algorytm może być też: | ||
*odważny (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) | |||
**przesunąć środek kuli poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów <math>x^{M(k)}-x^{k}=d</math> , tzn. ustalić środek nowej kuli w punkcie | |||
<math>x^{M(k)}=\alpha (x^{M(k)}-x^(k))+x^{(k)}, \alpha>1</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 55: | Linia 72: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd10.png|thumb|500px]] | ||
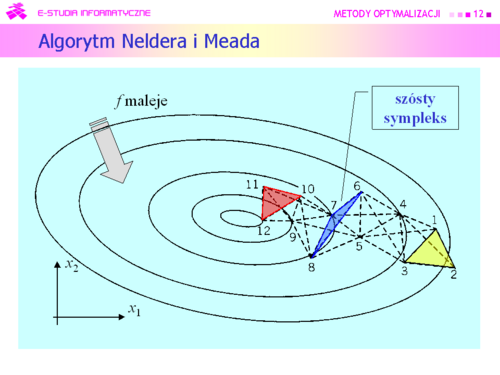
|valign="top"| | |valign="top"|Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez: | ||
J. A. Neldera i R. Meada i opublikowany w 1965 r. | |||
|} | |} | ||
---- | ---- | ||
| Linia 61: | Linia 80: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd11.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Nie będziemy zagłębiali się w szczegóły algorytmu Neldera i Meada (jak ustalić próbę początkową, jak będąc odważnym zachować niezbędny stopień ostrożności itd.) odsyłając Czytelnika np. do monografii A. Stachurski, A. Wierzbicki: Podstawy optymalizacji, Oficyna Wydawnicza PW 1999, rozdział 3.10. | ||
|} | |} | ||
---- | ---- | ||
| Linia 67: | Linia 86: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. | ||
|} | |} | ||
---- | ---- | ||
| Linia 73: | Linia 92: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd13.png|thumb|500px]] | ||
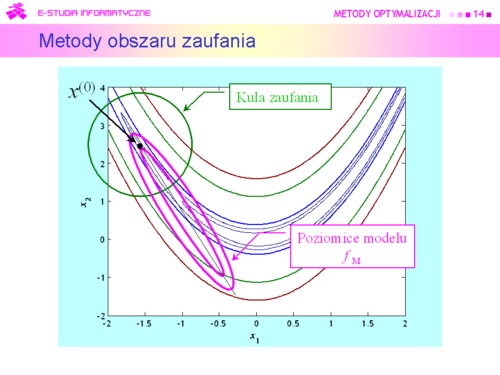
|valign="top"| | |valign="top"|Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się: | ||
'''Metodami obszaru zaufania | |||
(Trust region methods)''' | |||
|} | |} | ||
---- | ---- | ||
| Linia 79: | Linia 101: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Przyjmujemy zatem, że dookoła punktu bieżącego <math>x^(k)</math> została określona kula <math>\mathbb{K}\ (x, r)</math> i funkcja <math>x \mapsto f_M(x)</math> będąca modelem zachowania się funkcji wyboru f w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową | ||
<math>(APR)x \mapsto x^TQx+c^Tx+\sigma</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 85: | Linia 109: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd15.png|thumb|500px]] | ||
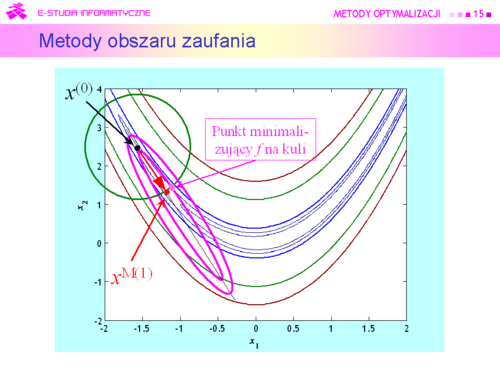
|valign="top"| | |valign="top"|W takiej sytuacji przeszukanie otoczenia może oznaczać tylko jedno – szukanie punktu <math>x^{M(k)}</math>, minimalizującego funkcję modelującą na kuli. | ||
Punkt ten oczywiście będzie się różnił od rzeczywistego minimum funkcji celu f na kuli zaufania, ale mamy nadzieję, że niewiele, a co ważniejsze będzie spełniona nierówność | |||
<math>f(x^{M(k)}<f(x^{k-1})</math> | |||
oznaczająca, że funkcja celu z kroku na krok maleje. | |||
|} | |} | ||
---- | ---- | ||
| Linia 91: | Linia 121: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd16.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd16.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Ponieważ punkt<math> x^{M(k)}</math> został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy – wartość funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób trzeba dostosowywać promień kuli do zmienności funkcji celu. Zauważmy też, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z ograniczeniami ale z prostą funkcją wyboru – kwadratową funkcją aproksymującą. | ||
|} | |} | ||
---- | ---- | ||
| Linia 97: | Linia 127: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd17.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W świetle ostatniej uwagi jest oczywiste, że algorytmy wykorzystujące omawiane podejście mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występujących w nich zadań | ||
<math>f_M(x)=x^TQx+c^Tx+\sigma \rightarrow min</math> | |||
<math>p.o.(x-x^{(k)})^T(x-x^(k))\le r^2</math> | |||
|} | |} | ||
---- | ---- | ||
| Linia 103: | Linia 138: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd18.png|thumb|500px]] | ||
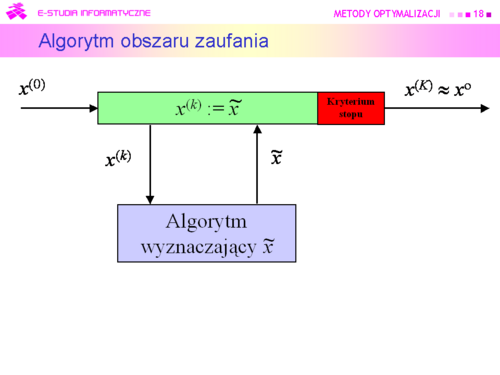
|valign="top"| | |valign="top"|'''Podstawowy algorytm obszaru zaufania''' | ||
Inicjalizacja | |||
Wybierz punkt początkowy <math>x^{(0)}</math>. | |||
Ustal początkowy obszar zaufania <math>T(x^{(0)}</math>). | |||
Podstaw k := 0. | |||
Kroki algorytmu | |||
#Dla punktu <math>x^{(k)}</math> wyznacz model f <math>M(\cdot; x^{(k)})</math> funkcji celu w jego otoczeniu. | |||
#Znajdź przybliżenie punktu <math>\tilde{x}^{(k)}</math> | |||
#Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw <math>\tildex^{(k)}:={x}^{(k)}</math> , idź do 5. W przeciwnym przypadku idź do 4. | |||
#Zmniejsz obszar zaufania do TS, podstaw <math>T(x^{(k)}) := TS</math>, idź do 2. | |||
#Jeżeli spełnione jest kryterium stopu, to<math> x^{(k)}</math> przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 6. | |||
#Sprawdź czy należy powiększyć obszar zaufania do TL. Jeżeli tak, podstaw | |||
<math>T(x^{(k)}) := TL</math>, idź do 7. W przeciwnym przypadku idź do 7. | |||
#Podstaw k := k + 1, idź do 1. | |||
Wyjaśnień wymagają kroki 2, 3, 6 i oczywiście kryterium stopu | |||
|} | |} | ||
---- | ---- | ||
| Linia 121: | Linia 174: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd21.png|thumb|500px]] | ||
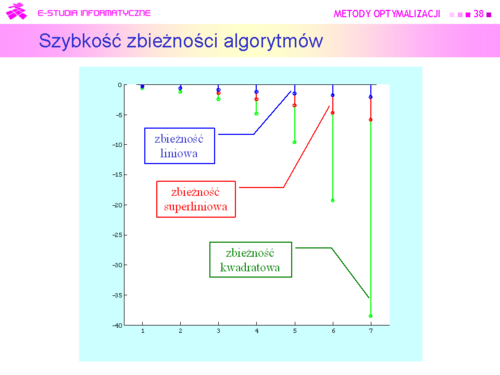
|valign="top"| | |valign="top"|Ciąg prostszych zadań daje ciąg rozwiązań <math>{ x^{(k)}_{k-0}^\infty}</math> Naturalne pytanie które postawiliśmy, to kiedy go uciąć – które k uznać za ostatnie, dające rozwiązanie z dostateczną dokładnością. Był to zasygnalizowany problem testu stopu. Związane z tym problemem jest pytanie drugie – czy wygenerowany ciąg w ogóle jest zbieżny, a gdy jest, to czy jego granica jest rozwiązaniem zadania optymalizacji ? Jest to pytanie teoretyczne i odpowiemy na nie po konkretyzacji algorytmu w wykładzie siódmym. | ||
|} | |} | ||
---- | ---- | ||
| Linia 127: | Linia 180: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd22.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd22.png|thumb|500px]] | ||
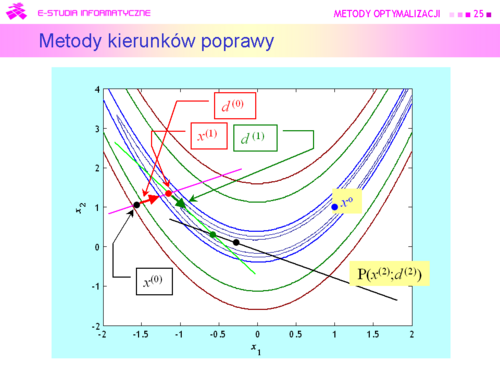
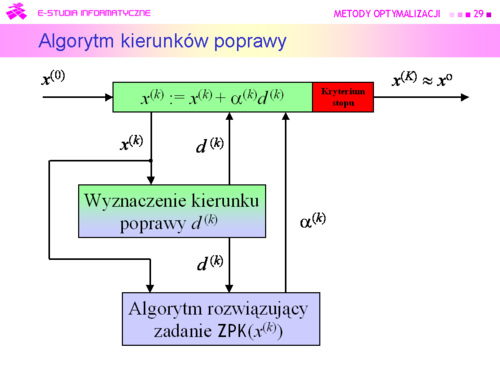
|valign="top"| | |valign="top"|Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3). | ||
Algorytm będzie zatem wykorzystywał: | |||
'''Metody kierunków poprawy''' | |||
|} | |} | ||
---- | ---- | ||
| Linia 133: | Linia 189: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd23.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd23.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek d jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający mniejszą niż w punkcie bieżącym wartość funkcji celu. | ||
|} | |} | ||
---- | ---- | ||
| Linia 145: | Linia 201: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu <math>\bar{x} \in P(x^{(k)};d)\subset R^n</math> jest równoważne ustaleniu pewnego <math>\bar{\alpha} \in R</math> Zatem zmieniając <math>\alpha </math> od zera do plus nieskończoności ruszamy się wzdłuż prostej <math>P(x^{(k)};d)</math> w kierunku malenia funkcji celu. Konkretną wartość <math>\bar{\alpha}</math> – długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze P(x(k);d) trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: wybieramy duży krok początkowy <math>\alpha ^{(0)}</math>, gdy <math>f(x^{(k)}+\alpha ^{(0)}d)<f(x^{(k)})</math> to <math>\alpha^{(0)}</math> uznajemy za długość kroku, gdy przeciwnie – zmniejszamy <math>\alpha^{(0)}</math> do <math>\alpha^{(1)}</math>), powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę | ||
|} | |} | ||
---- | ---- | ||
Wersja z 11:53, 25 wrz 2006
 |
 |
 |
 |
 |
Algorytm może być:
• ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) –przyjąć xM(k) za środek nowego otoczenia
|
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |