PF Moduł 14

Wykład 14 - Zjawiska elektromagnetyczne 14.1. Zjawisko indukcji elektromagnetycznej 14.2. Zjawisko samoindukcji 14.3 Energia pola magnetycznego 14.4. Elektromagnetyczne drgania swobodne 14.5. Elektromagnetyczne drgania tłumione 14.6. Elektromagnetyczne drgania wymuszone 14.7. Równania Maxwella w postaci całkowej 14.8. Operatory różniczkowe 14.9. Równania Maxwella w postaci różniczkowej 14.10-13. Materiały do ćwiczeń

---

14.1 Zjawisko indukcji elektromagnetycznej Zjawisko indukcji elektromagnetycznej odkryte przez Michaela Faradaya (1791-1867) polega na wzbudzaniu w zamkniętym obwodzie prądu indukcyjnego, pod wpływem zmian strumienia zewnętrznego pola magnetycznego. Bezpośrednią przyczyną przepływu prądu indukcyjnego jest powstająca w obwodzie siła elektromotoryczna $E=-\frac{d{\mathrm{\Phi }}_B}{dt}$ Reguła Lenza, określająca kierunek prądu indukcyjnego, wynika przede wszystkim z zasady zachowania energii. Przepływ prądu indukcyjnego jest oznaką, że w obwodzie pojawiła się energia. Zatem zmiana strumienia magnetycznego wymaga wykonania pracy przez siłę zewnętrzną, która tę zmianę wywołuje. Np. zbliżanie magnesu skierowanego biegunem N w stronę obwodu zwiększa strumień magnetyczny przenikający przez powierzchnię obwodu. Prąd indukcyjny popłynie w takim kierunku, żeby wytworzone przez niego pole magnetyczne odpychało zbliżający się magnes, a więc przed obwodem musi powstać biegun N. Reguła Lenza wynika również z bardzo ogólnej reguły przekory (Le Chatelier i Braun), która głosi, że układy fizyczne zachowują się przekornie. Układ fizyczny znajdujący się w stanie równowagii poddany działaniu czynnika zewnętrznego reaguje tak, żeby zmniejszyć wpływ tego czynnika ii osiągnać nowy stan równowagi możliwie niezbyt odległy od stanu równowagi wyjściowej. Zjawisko indukcji elektromagnetycznej jest jednym z wielu zjawisk fizycznych, których przebieg wynika z reguły przekory.

---

14.2 Zjawisko samoindukcji Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie $I(t)$ to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy $B(t)=\frac{{\mu }_0{\mu }_{r}N}{l}I(t)$ oraz wartość strumienia magnetycznego przez powierzchnię każdego zwoju ${\mathrm{\Phi }}_B(t)=B\cdot S=\frac{{\mu }_0{\mu }_{r}NS}{l}I(t)$ a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości $E_z=-\frac{d{\mathrm{\Phi }}_B}{dt}$ Zatem całkowita siła elektromotoryczna powstająca w zwojnicy $E=-N\frac{d{\mathrm{\Phi }}_B}{dt}$ Po podstawieniu i przekształceniu otrzymujemy wzór $E=-L\frac{dl}{dt}$ z którego wynika zależność wartości siły elektromotorycznej samoindukcji od szybkości zmiany natężenia prądu, oraz od indukcyjności zwojnicy $L=\frac{{\mu }_0{\mu }_r{N}^{2}S}{l}$ czyli współczynnika zależnego od parametrów zwojnicy, określającego zdolność zwojnicy do wytwarzania siły elektromotorycznej samoindukcji. Dużą wartość $L$ można uzyskać dla zwojnicy o dużej liczbie zwojów, z rdzeniem ferromagnetycznym (duża wartość ${\mu }_r$). Zjawisko samoindukcji może zachodzić w każdym obwodzie, w którym płynie prąd o zmieniającym się w czasie natężeniu. Indukcyjność $L$ obwodu zależy od kształtu i rozmiarów obwodu oraz od obecności materiału ferromagnetycznego.

---

14.3 Energia pola magnetycznego W chwili $t_0=0$ zamykamy klucz i w obwodzie RL zaczyna płynąć prąd o rosnącym natężeniu, spełniającym równanie $U_0-L\frac{dI}{dt}-RI=0$ którego rozwiązaniem jest funkcja $I(t)\frac{U_0}{R}(1-e^{-(t/\tau )})$ gdzie $\tau$ jest stałą czasową procesu narastania natężenia prądu do wartości wynikającej z prawa Ohma. Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez $I$ $U_{0}I=LI\frac{dI}{dt}+R{I}^2$ Iloczyn natężenia prądu i napięcia źródła $U_{0}I=P$ to moc źródła Składnik $R{I}^2=P_R$ to moc w oporniku. Zatem wyrażenie $LI\frac{dI}{dt}=P_B=\frac{d{W}_B}{dt}$ to moc w zwojnicy, czyli szybkość zmiany energii pola magnetycznego we wnętrzu zwojnicy. Po scałkowaniu otrzymujemy wzór określający energię pola magnetycznego wewnątrz zwojnicy $W_B=\frac{1}{2}L{I}^2$ Wykorzystując wzory $L=\frac{{\mu }_0{\mu }_r{N}^{2}S}{l}$ $B=\frac{{\mu }_0{\mu }_{r}N}{l}I$ otrzymamy zależność energii pola magnetycznego od wartości wektora indukcji magnetycznej $W_B=\frac{1}{2}\frac{1}{{\mu }_0{\mu }_r}{B}^{2}V$ gdzie $V$ jest objętością, oraz wzór określający przestrzenną gęstość energii pola magnetycznego $\frac{W_B}{V}=\frac{1}{2}\frac{1}{{\mu }_0{\mu }_r}{B}^2$ $w_B=\frac{1}{2}\overrightarrow{H}\cdot \overrightarrow{B}$

---

14.4 Elektromagnetyczne drgania swobodne Modelowym układem fizycznym, w którym zachodzić mogą elektromagnetyczne drgania harmoniczne swobodne jest zamknięty obwód elektryczny o oporności równej zeru, zawierający zwojnicę o indukcyjności $L$ i kondensator o pojemności $C$. W obwodzie przedstawionym na rysunku kondensator został naładowany ładunkiem $q_0$. Gdy w chwili $t=0$ zamkniemy obwód, to kondensator zacznie się rozładowywać i zmieniający się prąd rozładowania spowoduje powstanie w zwojnicy siły elektromotorycznej samoindukcji. Stan fizyczny obwodu można opisać za pomocą II prawa Kirchhoffa: $L\frac{dI}{dt}+\frac{q}{C}=0$ gdzie $I=\frac{dq}{dt}$ Po podstawieniach i przekształceniach otrzymujemy równanie elektromagnetycznego oscylatora harmonicznego swobodnego $\frac{d^{2}q}{d{t}^2}=-\frac{1}{LC}q$ Rozwiązaniem tego równania, spełniającym warunki początkowe: $q(0)=q_0$ , $I(0)=0$ jest funkcja Parser nie mógł rozpoznać (nieznana funkcja „\dispaystyle”): {\displaystyle \dispaystyle q(t)=q_0 cos\omega_0 t} gdzie: Parser nie mógł rozpoznać (nieznana funkcja „\dispaystyle”): {\displaystyle \dispaystyle \omega_0=\sqrt{\displaystyle \frac{1}{LC}}} - częstość drgań swobodnych, ${\omega }_{0}t$ - faza drgań, $q_0$ - amplituda drgań. Mając funkcję $q(t)$ można obliczyć napięcie na kondensatorze $U_C(t)$, natężenie prądu $I(t)$ oraz napięcie na zwojnicy $U_L(t)$: $\begin{array}{cc}{U}_C(t)=\frac{q(t)}{C}=\frac{q_0}{C}cos{\omega }_{0}t=(U_C{)}_{0}cos{\omega }_{0}t& (U_C{)}_0=\frac{q_0}{C}\end{array}$ $\begin{array}{cc}I(t)=\frac{dq}{dt}=I_{0}cos({\omega }_{0}t+\pi /2)& I_0=q_0{\omega }_0\end{array}$ $\begin{array}{cc}{U}_L(t)=L\frac{dI}{dt}=(U_L{)}_{0}cos({\omega }_{0}t+\pi )& (U_L{)}_0=\frac{q_0}{C}\end{array}$ Warto zauważyć, że napięcia na kondensatorze i zwojnicy mają równe amplitudy i przeciwne fazy (przesunięcie fazowe wynosi $-\pi$), zaś natężenie prądu jest przesunięte w fazie o $-\pi /2$. Z powyższej analizy wynika, że po dostarczeniu do obwodu LC porcji energii (naładowanie kondensatora) i braku dalszej ingerencji zewnętrznej, zachodzą w nim drgania harmoniczne swobodne - wielkości opisujące stan układu są funkcjami harmonicznymi. Porównanie z mechanicznym oscylatorem harmonicznym swobodnym (np. klocek o masie m zaczepiony do sprężyny o współczynniku sprężystości k) pokazuje, że ładunek na kondensatorze jest wielkością analogiczną do wychylenia z położenia równowagi a natężenie prądu do prędkości. Pełne zestawienie analogii między drganiami elektromagnetycznymi i drganiami mechanicznymi przedstawiono w tabeli nr 14.1. Okres i częstotliwość drgań swobodnych (inaczej drgań własnych) obwodu LC są równe: Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle \displaystyle T_0=\frac{2\pi}{\omeha_0}=2\pi \sqrt{LC}} ${\nu }_0=\frac{1}{T_0}=\frac{1}{2\pi }\sqrt{\frac{1}{LC}}$ Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy, a zatem możemy obliczyć moc $P_E$ i energię $W_E$ pola elektrycznego w kondensatorze $P_E=\frac{W_E}{dt}=U_{C}I=\frac{q}{C}\cdot I$ $W_E=\int \frac{q}{C}dq=\frac{1}{2C}\cdot q^2=\frac{1}{2C}\cdot q_0^{2}co{s}^2{\omega }_{0}t$ oraz moc $P_B$ i energię $W_B$ pola magnetycznego w zwojnicy $P_B=\frac{W_B}{dt}=U_{L}I=L\frac{dI}{dt}\cdot I$ $W_B=\int LIdI=\frac{1}{2}L{I}^2=\frac{1}{2C}\cdot q_0^{2}si{n}^2{\omega }_{0}t$ Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o <mathpi/2\,</math>. Całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy $W=W_A+W_B=\frac{1}{2C}\cdot q^2+\frac{1}{2}L\cdot I^2=\frac{1}{2C}\cdot q_0^2=const.$ jest stała i równa energii dostarczonej do obwodu. Z powyższych rozważań wynika, że elektromagnetyczne drgania swobodne w obwodzie LC można traktować jak okresowe przemiany energii pola elektrycznego w kondensatorze w energię pola magnetycznego w zwojnicy i na odwrót. Okres tych przemian jest równy połowie okresu drgań własnych czyli okresu zmienności napięć na kondensatorze i zwojnicy oraz natężenia prądu. W rzeczywistych obwodach elektrycznych występuje zawsze niezerowy opór elektryczny, a więc wydziela się energia cieplna. W takim przypadku energia układu drgającego maleje i po pewnym czasie drgania zanikają.

---

14.5 Elektromagnetyczne drgania tłumione Drgania harmoniczne tłumione mogą zachodzić w obwodach elektrycznych zawierających elementy $R,L,C$. Załóżmy, że naładowany kondensator o pojemności $C$ zaczyna się rozładowywać przez opór $R$ i zwojnicę o indukcyjności $L$. Zgodnie z drugim prawem Kirchoffa suma zmian potencjału na drodze zamkniętej jest równa zeru $RI+L\frac{dI}{dt}+\frac{q}{C}=0$ Po podstawieniu i podzieleniu stronami przez L otrzymamy równanie $\frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=0$ Jest to równanie elektromagnetycznego oscylatora harmonicznego tłumionego, w którym $\frac{1}{LC}={\omega }_0^2$ oraz $\frac{R}{2L}=\beta$ Gdy spełniony jest warunek $\beta <{\omega }_0$ to rozwiązaniem tego równania różniczkowego jest funkcja “okresowa” $q(t)=q_0{e}^{-\beta t}cos{\omega }_{t}t$ ${\omega }_t=\sqrt{{\omega }_0^2-{\beta }^2}$ zatem ładunek elektryczny w kondensatorze wykonywać będzie drgania tłumione. Na rysunku przedstawiono porównanie drgań swobodnych i tłumionych, dla kilku wartości współczynnika tłumienia. Warto zauważyć, że szybkość zaniku amplitudy drgań silnie zależy od współczynnika tłumienia $\beta$. Natomiast istotny wpływ na częstość drgań tłumionych pojawia się dopiero dla wartości współczynnika tłumienia $\beta$ bliskich wartości granicznej, czyli ${\omega }_0$. Podstawowe różnice między drganiami tłumionymi i drganiami swobdnymi: amplituda drgań maleje eksponencjalnie z upływem czasu, częstość drgań tłumionych jest mniejsza od częstości drgań swobodnych, całkowita energia oscylatora maleje z upływem czasu Gdy spełniony jest warunek $\beta \ge {\omega }_0$ rozwiązaniem równania różniczkowego jest funkcja aperiodyczna. Rozładowanie kondensatora jest eksponencjalne i jednorazowe.

---

14.6 Elektromagnetyczne drgania wymuszone Elektromagnetyczne drgania wymuszone można zaobserować w obwodzie RLC (zawierającym zwojnicę o indukcyjności $L$, kondensator o pojemności $C$ oraz opornik o oporności $R$) do którego dołączone zostało źródło napięcia sinusoidalnego. Stan fizyczny tego układu opisuje w dowolnej chwili II prawo Kirchhoffa: $L\frac{dI}{dt}+RI+\frac{q}{C}=U_{0}sin\omega t$ Po podzieleniu równania przez $L$ i podstawieniu $\begin{array}{ccc}\frac{dq}{dt}=I& \frac{R}{2L}=\beta & \frac{1}{LC}={\omega }_0^2\end{array}$ gdzie: $\beta$ - współczynnik tłumienia, ${\omega }_0$ - częstość drgań swobodnych, otrzymujemy równanie elektromagnetycznych drgań wymuszonych $\frac{d^{2}q}{d{t}^2}+2\beta \frac{dq}{dt}+{\omega }_0^2=\frac{U_0}{L}sin\omega t$ W równaniu tym bezpośrednie parametry układu fizycznego jakimi są w przypadku obwodu RLC: indukcyjność $L$, pojemność $C$ i oporność $R$ zostały zastąpione przez uniwersalne parametry występujące w opisie drgań harmonicznych dowolnego układu fizycznego (np. oscylator harmoniczny mechaniczny), a mianowicie przez częstość drgań własnych ${\omega }_0$ i współczynnik tłumienia $\beta$. Ponieważ napięcie wymuszające jest sinusoidalną funkcją czasu, to rozwiązania tego równania poszukujemy w postaci funkcji $q(t)=q_{0}sin(\omega t-\phi )$ a zatem przewidujemy, że ładunek na kondensatorze będzie się zmieniać sinusoidalnie z częstością taką jak częstość napięcia wymuszającego oraz, że będzie przesunięty w fazie o $\phi$ względem tego napięcia. Po podstawieniu przewidywanej funkcji $q(t)$ do równania i zażądaniu aby równanie to stało się tożsamością (funkcja $q(t)$ musi spełniać to równanie w każdej chwili czasu) otrzymamy wzory określające amplitudę ładunku $q_0$ i przesunięcie fazowe $\phi$ : $q_0=\frac{U_0/L}{\sqrt{({\omega }_0^2-{\omega }^2{)}^2}+4{\beta }^2{\omega }^2}$ $\phi =arctg\frac{2\beta \omega }{{\omega }_0^2-{\omega }^2}$ Przy ustalonych parametrach układu $R,L,C$ (a więc również ${\omega }_0$ i $\beta$) amplituda ładunku oraz przesunięcie fazowe są funkcjami częstości  napięcia wymuszającego. Po przeprowadzeniu badania funkcji $q_0(\omega )$ można stwierdzić, że amplituda ładunku na kondensatorze osiąga wartość maksymalną dla częstości wymuszania ${\omega }_r$ określonej wzorem ${\omega }_r=\sqrt{{\omega }_0^2-2{\beta }^2}$ gdy spełniony jest warunek $\beta <{\omega }_0\frac{\sqrt{2}}{2}={\beta }_g$ Zjawisko wymuszania drgań z taką częstością przy której amplituda drgań osiąga wartość maksymalną nazywamy rezonansem. Rezonans w obwodzie RLC zachodzi przy częstości wymuszania ${\omega }_r$ zwanej częstością rezonansową, gdy współczynnik tłumienia $\beta$ jest mniejszy od wartości granicznej ${\beta }_g$. Gdy tłumienie jest większe $(\beta >{\beta }_g)$ układu RLC nie udaje się wprowadzić w stan rezonansu. Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami: $(q_0{)}_{max}=\frac{U_0/L}{2\beta \sqrt{{\omega }_0^2-{\beta }^2}}$ ${\phi }_r=arctg\frac{\sqrt{{\omega }_0^2-{\beta }^2}}{\beta }$ Szczególny przypadek rezonansu występuje w przypadku gdy współczynnik tłumienia $\beta =0$. Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych ${\omega }_r={\omega }_0$ i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym ${\omega }_r=\pi /2$. W takiej sytuacji dochodzi przeważnie do zniszczenia układu drgającego zanim amplituda drgań osiągnie wartość nieskończoną. Graniczne wartości amplitudy drgań $q_0$ i przesunięcia fazowego  dla częstości wymuszania dążącej do zera wynoszą: $\begin{array}{cc}\underset{\omega \to 0}{\lim }{q}_0=U_{0}C& \underset{\omega \to 0}{\lim }\phi =0\end{array}$ Dla częstości znacznie przekraczających częstość własną, wartości graniczne amplitudy drgań i przesunięcia fazowego wynoszą: $\begin{array}{cc}\underset{\omega \to \mathrm{\infty }}{\lim }{q}_0=0& \underset{\omega \to \mathrm{\infty }}{\lim }\phi =0\end{array}$ Warto jeszcze zaznaczyć, że niezależnie od wartości współczynnika tłumienia, przesunięcie fazowe $\phi$ osiąga wartość $\pi /2$ przy częstości wymuszania $\omega$ równej częstości drgań własnych układu ${\omega }_0$. Wzory opisujące drgania wymuszone i rezonans można zapisać w uniwersalnej postaci bezwymiarowej, słusznej zarówno dla drgań elektromagnetycznych, jak i dla drgań mechanicznych. W tym celu wprowadza się tzw. parametry zredukowane: zredukowany współczynnik tłumienia $u=\frac{\beta }{{\omega }_0}$ zredukowana częstość drgań $w=\frac{\omega }{{\omega }_0}$ zredukowana amplituda drgań wymuszonych $X=\frac{q_0(\omega )}{q_0(\omega \to 0)}=\frac{q_0(\omega )}{U_{0}C}$ Po zastosowaniu powyższych podstawień wzory określające: amplitudę drgań i przesunięcie fazowe dla dowolnej częstości wymuszania, częstość rezonansową oraz amplitudę drgań i przesunięcie fazowe w stanie rezonansu przyjmą postać: $\begin{array}{cc}X=\frac{1}{\sqrt{(1-w^2{)}^2}+4u^2{w}^2}& \phi =arctg\frac{2uw}{1-w^2}\end{array}$ $w_r=\sqrt{1-2u^2}$ $\begin{array}{cc}{X}_r=X(w_r)=\frac{1}{2u\sqrt{1-2u^2}}& {\phi }_r=\phi (w_r)=arctg\frac{\sqrt{1-2u^2}}{u}\end{array}$ Na slajdzie przedstawiono wykresy zależności zredukowanej amplitudy drgań $X$ od zredukowanej częstości drgań w dla kilku wartości zredukowanego współczynnika tłumienia $u$. W miarę wzrostu współczynnika tłumienia rezonans pojawia się dla częstości coraz mniejszych i wartość amplitudy drgań w stanie rezonansu jest coraz mniejsza. Po przekroczeniu granicznej wartości współczynnika tłumienia rezonans nie pojawia się (krzywa $X(w)$ nie posiada maksimum). 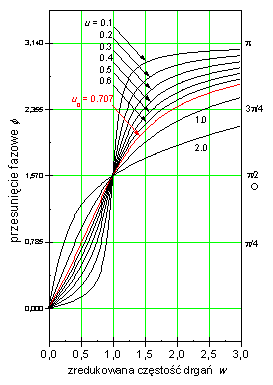Pierwszy wykres prezentuje zależność przesunięcia fazowego $\phi$ od zredukowanej częstości drgań $w$ dla kilku wartości zredukowanego współczynnika tłumienia $u$. 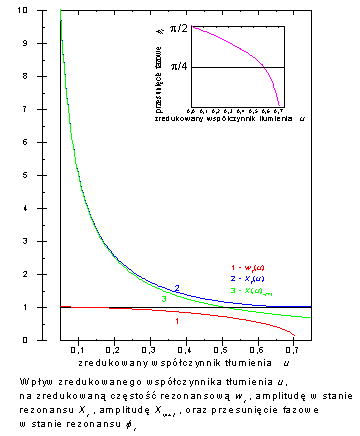Wykresy przedstawione na drugim rysunku pokazują wpływ zredukowanego współczynnika tłumienia u na zredukowaną częstość rezonansową $w_r$, zredukowaną amplitudę drgań $X_r$ i przesunięcie fazowe ${\omega }_r$ w stanie rezonansu oraz na zredukowaną amplitudę $X$ dla $w=1$. Warto zauważyć, że dla małych wartości współczynnika tłumienia amplituda drgań wymuszonych (amplituda ładunku) w stanie rezonansu $X_r$ jest funkcją szybkozmienną, zaś częstość rezonansowa funkcją wolnozmienną (jej wartość jest bliska częstości własnej układu). Gdy współczynnik tłumienia zbliża się do wartości granicznej, to - odwrotnie - amplituda drgań jest niemal stała (bliska wartości granicznej dla częstości wymuszania bliskiej zero, zaś częstość rezonansowa wr jest funkcją szybkozmienną. Wartość zredukowanej amplitudy $X$ dla $w=1$ jest mniejsza od $X_r$. Znając funkcję $q(t)$ można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego: napięcie na kondensatorze, natężenie prądu, napięcie na oporniku oraz napięcie na zwojnicy (p. Przykład 14.2). Niezależność amplitud ładunku i natężenia prądu oraz przesunięć fazowych względem napięcia wymuszającego oznacza, że zachodzą tzw. drgania ustalone. Układ fizyczny dopasowuje się do czynnika wymuszającego. Można łatwo wykazać, że podczas drgań ustalonych szybkość dostarczania energii przez źródło napięcia wymuszającego zrównuje się z szybkością strat energii na pracę prądu w oporniku i suma średniej energii pola elektrycznego w kondensatorze i średniej energii pola magnetycznego w zwojnicy jest stała (dla danej częstości wymuszania).

---

14.7 Równania Maxwella w postaci całkowej Równania i prawa Maxwella powstały w roku 1864 przez modyfikacje i uogólnienia praw opisujących wyniki obserwacji doświadczalnych zjawisk elektromagnetycznych. Prawo Gaussa dla pola elektrycznego wytworzonego przez ładunki elektryczne ${\oint }_S\overrightarrow{D}\cdot d\overrightarrow{S}=\underset{V}{\int }\rho dV$ Całkowity strumień wektora indukcji pola elektrycznego przez zamknietą powierzchnię jest równy ładunkowi zawartemu w otoczonej przez tę powierzchnię objętości. Pole elektryczne jest polem źródłowym - źródłem pola elektrycznego jest ładunek elektryczny. Ze wzoru wyrażającego w postaci całkowej związek między natężeniem pola i potencjałem wynika, że w polu elektrycznym wytworzonym przez ładunki ${\oint }_L\overrightarrow{E}d\overrightarrow{l}=0$ , a więc pole wytworzone przez ładunki jest polem bezwirowym (linie sił pola mają początek i koniec). Prawo Gaussa dla pola magnetycznego ${\oint }_S\overrightarrow{B}\cdot d\overrightarrow{S}=0$ Całkowity strumień wektora indukcji pola magnetycznego przez zamknietą powierzchnię jest równy zeru. Pole magnetyczne jest polem bezźródłowym. Nie istnieją monopole magnetyczne. I prawo Maxwella (uogólnione prawo Faradaya) - wirowe pole elektryczne ${\oint }_L\overrightarrow{E}\cdot d\overrightarrow{l}=-\frac{\partial }{\partial t}\underset{S}{\int }\overrightarrow{B}\cdot d\overrightarrow{S}$ Cyrkulacja wektora natężenia pola elektrycznego wzdłuż zamkniętej krzywej $L$ jest równa szybkości zmiany (ze znakiem ujemnym) strumienia wektora indukcji pola magnetycznego przez powierzchnię $S$, ograniczoną przez krzywą $L$. Wir pola elektrycznego jest powiązany z wektorową zmianą pola magnetycznego za pomocą reguły śruby prawoskrętnej, z uwzględnieniem znaku minus po prawej stronie równania. Wskutek zmiany strumienia pola magnetycznego powstaje wirowe pole elektryczne (linie sił pola są krzywymi zamkniętymi). Takie pole elektryczne jest polem bezźródłowym, tzn. w takim polu strumień wektora indukcji elektrycznej przez zamknietą powierzchnię jest równy zeru ${\oint }_S\overrightarrow{D}d\overrightarrow{S}=0$. II prawo Maxwella (uogólnione prawo Ampere’a) - wirowe pole magnetyczne ${\oint }_L\overrightarrow{D}\cdot d\overrightarrow{l}=\underset{S}{\int }\overrightarrow{j}\cdot d\overrightarrow{S}+\frac{\partial }{\partial t}\overrightarrow{D}\cdot d\overrightarrow{S}$ Cyrkulacja wektora natężenia pola magnetycznego wzdłuż zamkniętej krzywej L jest równa sumie natężenia prądu przepływającego przez powierzchnię S, ograniczoną przez krzywą L oraz szybkości zmiany strumienia wektora indukcji pola elektrycznego przez powierzchnię S, ograniczoną przez tę krzywą, czyli natężenia tzw. prądu przesunięcia.

---

---

---

---

---

---