MN02LAB: Różnice pomiędzy wersjami
m MN Ćwiczenia 2 moved to MN02LAB |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
<!-- | <!-- | ||
Konwertowane z pliku LaTeX przez latex2mediawiki, zob. http://www.ii.uj.edu.pl/ pawlik1/latex2mediawiki.php | Konwertowane z pliku LaTeX przez latex2mediawiki, zob. http://www.ii.uj.edu.pl/ pawlik1/latex2mediawiki.php | ||
| Linia 15: | Linia 14: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | ||
Powtarzając rachunki z dowodu lokalnej zbieżności, możemy łatwo stwierdzić, że kolejne | Powtarzając rachunki z dowodu lokalnej zbieżności, możemy łatwo stwierdzić, że kolejne | ||
iteracje dają <math>\displaystyle x_k</math> które także spełniają warunek <math>\displaystyle x_k - x^* > 0</math>. Ponadto | iteracje dają <math>\displaystyle x_k</math>, które także spełniają warunek <math>\displaystyle x_k - x^* > 0</math>. Ponadto | ||
nietrudno sprawdzić, że <math>\displaystyle x_{k+1} < x_k</math>, a więc mamy ciąg malejący i | nietrudno sprawdzić, że <math>\displaystyle x_{k+1} < x_k</math>, a więc mamy ciąg malejący i | ||
ograniczony. Jego granicą musi być <math>\displaystyle x^*</math> (dlaczego?). | ograniczony. Jego granicą musi być <math>\displaystyle x^*</math> (dlaczego?). | ||
| Linia 27: | Linia 26: | ||
Newtona do rozwiązania równania <math>\displaystyle z^n-1=0</math> w dziedzinie zespolonej. Punkt <math>\displaystyle z_0 = | Newtona do rozwiązania równania <math>\displaystyle z^n-1=0</math> w dziedzinie zespolonej. Punkt <math>\displaystyle z_0 = | ||
(x_0,y_0)</math> należy do <strong>basenu zbiezności metody</strong>, jeśli metoda Newtona jest | (x_0,y_0)</math> należy do <strong>basenu zbiezności metody</strong>, jeśli metoda Newtona jest | ||
z nim zbieżna do (jakiegokolwiek) pierwiastka w/w równania. Kolor odpowiadający | |||
<math>\displaystyle z_0</math> jest określany na podstawie liczby iteracji potrzebnych metodzie do | <math>\displaystyle z_0</math> jest określany na podstawie liczby iteracji potrzebnych metodzie do | ||
zbieżności. | zbieżności. | ||
Zupełnie miłym (i estetycznie wartościowym) doświadczeniem | Zupełnie miłym (i estetycznie wartościowym) doświadczeniem jest napisanie | ||
programu w Octave, który wyświetla baseny zbieżności metody Newtona | programu w Octave, który jak poniżej wyświetla baseny zbieżności metody Newtona. | ||
[[Image:MNfraktal.png|thumb|450px|center|Basen zbieżności metody Newtona w okolicy początku układu | [[Image:MNfraktal.png|thumb|450px|center|Basen zbieżności metody Newtona w okolicy początku układu | ||
| Linia 63: | Linia 62: | ||
równania <math>\displaystyle x^2 = a</math>. Zaprogramuj tę metodę i sprawdź, jak wiele dokładnych cyfr | równania <math>\displaystyle x^2 = a</math>. Zaprogramuj tę metodę i sprawdź, jak wiele dokładnych cyfr | ||
wyniku dostajesz w kolejnych krokach. Czy to możliwe, by liczba dokładnych cyfr | wyniku dostajesz w kolejnych krokach. Czy to możliwe, by liczba dokładnych cyfr | ||
znaczących z grubsza podwajała się na każdej iteracji? Wskaż takie <math>\displaystyle a</math> dla | znaczących z grubsza podwajała się na każdej iteracji? Wskaż takie <math>\displaystyle a</math>, dla | ||
którego to nie będzie prawdą. | którego to nie będzie prawdą. | ||
| Linia 69: | Linia 68: | ||
<div style="font-size:smaller; background-color:#efe"> Na pewno kusi Cię, by zaprogramować najpierw ogólnie funkcję "metoda | <div style="font-size:smaller; background-color:#efe"> Na pewno kusi Cię, by zaprogramować najpierw ogólnie funkcję "metoda | ||
Newtona", a następnie przekazać jej jako parametr naszą funkcję. To oczywiście | Newtona", a następnie przekazać jej jako parametr naszą funkcję. To oczywiście | ||
będzie działać | będzie działać. W dodatku praktycznie tak samo szybko jak drugi sposób, w którym po prostu | ||
wyliczysz na karteczce wzór na iterację dla <strong>tej konkretnej funkcji, <math>\displaystyle F(x) = | wyliczysz na karteczce wzór na iterację dla <strong>tej konkretnej funkcji, <math>\displaystyle F(x) = | ||
x^2-a</math></strong> i potem go zaimplementujesz. Jednak | x^2-a</math></strong> i potem go zaimplementujesz. Jednak | ||
| Linia 96: | Linia 95: | ||
znaczących wyniku. | znaczących wyniku. | ||
Ale jeśli <math>\displaystyle a=0</math> to metoda zbieżna jest już tylko liniowo (z ilorazem 0.5 --- bo | Ale jeśli <math>\displaystyle a=0</math>, to metoda zbieżna jest już tylko liniowo (z ilorazem 0.5 --- bo | ||
jaki wtedy jest wzór na iterację?), | jaki wtedy jest wzór na iterację?), co mniej więcej trzy kroki będziemy więc | ||
dostawali kolejne zero dokładnego wyniku <math>\displaystyle x^*=0</math>. | dostawali kolejne zero dokładnego wyniku <math>\displaystyle x^*=0</math>. | ||
| Linia 106: | Linia 105: | ||
<div class="exercise"> | <div class="exercise"> | ||
Aby wyznaczyć <math>\displaystyle 1/a</math> dla <math>\displaystyle a>0</math> bez dzielenia(!) | Aby wyznaczyć <math>\displaystyle 1/a</math> dla <math>\displaystyle a>0</math> bez dzielenia(!) można zastosować metodę Newtona | ||
do funkcji <math>\displaystyle f(x) = 1/x - a</math>. Pokaż, że na <math>\displaystyle k</math>-tym kroku iteracji, | do funkcji <math>\displaystyle f(x) = 1/x - a</math>. Pokaż, że na <math>\displaystyle k</math>-tym kroku iteracji, | ||
<center><math>\displaystyle | <center><math>\displaystyle | ||
| Linia 143: | Linia 142: | ||
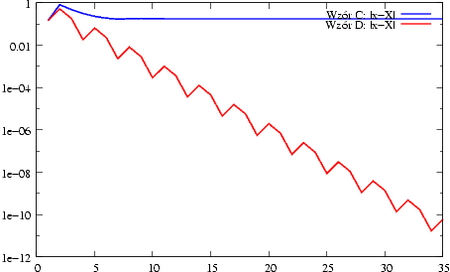
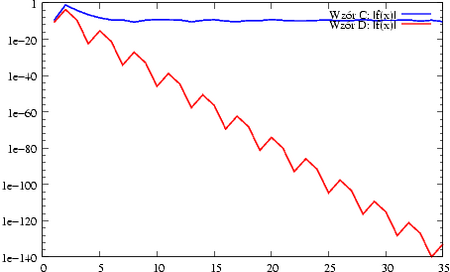
wzorem D.]] | wzorem D.]] | ||
Jak wyjaśnić te wyniki? Czy możesz już być | Jak wyjaśnić te wyniki? Czy możesz już być pewien, że masz dobrą implementację? | ||
</div></div> | </div></div> | ||
| Linia 152: | Linia 151: | ||
<math>\displaystyle \sin</math>, dawać komunikat o błędzie dla <math>\displaystyle \sin^2</math> (bo nie ma przeciwnych znaków). | <math>\displaystyle \sin</math>, dawać komunikat o błędzie dla <math>\displaystyle \sin^2</math> (bo nie ma przeciwnych znaków). | ||
Zapewne | Zapewne zauważyłeś, że wzory A i B są matematycznie równoważne, podobnie zresztą | ||
jak wzory C i D. Niestety, tylko wzór A i C dają w efekcie dobre przybliżenia | jak wzory C i D. Niestety, tylko wzór A i C dają w efekcie dobre przybliżenia | ||
miejsca zerowego, podczas gdy wzory B i D prowadzą do oszacowania na miejsce | miejsca zerowego, podczas gdy wzory B i D prowadzą do oszacowania na miejsce | ||
| Linia 159: | Linia 158: | ||
Wyjaśnieniem tego fenomenu jest zjawisko redukcji cyfr przy odejmowaniu. | Wyjaśnieniem tego fenomenu jest zjawisko redukcji cyfr przy odejmowaniu. | ||
Jeśli chodzi o pewność... No cóż, | Jeśli chodzi o pewność... No cóż, sprawdziłeś, że <strong>działa</strong> w przypadkach, | ||
dla których | dla których spodziewałeś się, że będzie działać. Że tam, gdzie spodziewałeś się | ||
kłopotów, lub komunikatu o błędzie --- tak rzeczywiście się stało. Wreszcie, | kłopotów, lub komunikatu o błędzie --- tak rzeczywiście się stało. Wreszcie, | ||
potwierdziłeś, że zachowanie metody jest zgodne z jej znanymi właściwościami. | |||
Tak więc, można <strong>przypuszczać</strong>, że implementacja jest poprawna.... | Tak więc, można <strong>przypuszczać</strong>, że implementacja jest poprawna.... | ||
Wersja z 18:17, 19 wrz 2006
Ćwiczenia: równania nieliniowe skalarne
Ćwiczenie: Metoda Newtona może być zbieżna globalnie
Wykaż, że jeśli jest rosnąca i wypukła na oraz dla , to metoda Newtona startująca z jest zbieżna.
Ćwiczenie: Fraktale
Ciekawy zbiór o charakterze fraktalnym powstaje w wyniku zastosowania metody Newtona do rozwiązania równania w dziedzinie zespolonej. Punkt należy do basenu zbiezności metody, jeśli metoda Newtona jest z nim zbieżna do (jakiegokolwiek) pierwiastka w/w równania. Kolor odpowiadający jest określany na podstawie liczby iteracji potrzebnych metodzie do zbieżności.
Zupełnie miłym (i estetycznie wartościowym) doświadczeniem jest napisanie programu w Octave, który jak poniżej wyświetla baseny zbieżności metody Newtona.

Ćwiczenie: Pierwiastkowanie
Niech . Aby wyznaczyć , można skorzystać z metody Newtona dla równania . Zaprogramuj tę metodę i sprawdź, jak wiele dokładnych cyfr wyniku dostajesz w kolejnych krokach. Czy to możliwe, by liczba dokładnych cyfr znaczących z grubsza podwajała się na każdej iteracji? Wskaż takie , dla którego to nie będzie prawdą.
Ćwiczenie: Odwrotność bez dzielenia
Aby wyznaczyć dla bez dzielenia(!) można zastosować metodę Newtona do funkcji . Pokaż, że na -tym kroku iteracji,
Dla jakich metoda będzie zbieżna do , a dla jakich nie? Oceń, ile iteracji potrzeba do spełnienia warunku , gdy ,
Ćwiczenie
Zaimplementuj metodę bisekcji. Sprawdź, jak będzie działać m.in. dla funkcji
- ,
- ,
- (wzór A),
- (wzór B),
- (wzór C),
- (wzór D),
gdy tolerancję błędu zadasz na poziomie .
Jak wyjaśnić te wyniki? Czy możesz już być pewien, że masz dobrą implementację?
Ćwiczenie
Wskaż wszystkie wartości , dla jakich metoda Newtona będzie zbieżna do rozwiązania równania
Wyznacz wartość , z którego startując powinieneś dostać ciąg oscylujący . Sprawdź eksperymentalnie, czy tak jest rzeczywiście.