Zaawansowane algorytmy i struktury danych/Ćwiczenia 7: Różnice pomiędzy wersjami
| Linia 51: | Linia 51: | ||
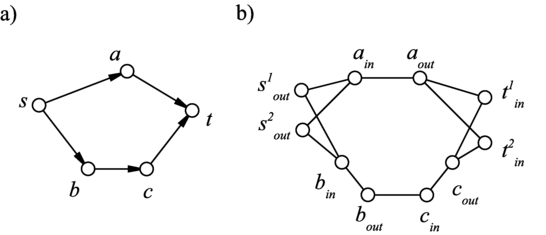
Dla każdego wierzchołka trzeba wykonać transformację przedstawioną na poniższym rysunku. | Dla każdego wierzchołka trzeba wykonać transformację przedstawioną na poniższym rysunku. | ||
{{ramka|1=[[Grafika: | {{ramka|1=[[Grafika:zasd_planar-path-transformation.png|500px|center]]|2= | ||
Transformacja grafu a) transformowany wierzchołek b) podgraf skonstruowany na podstawie tego wierzchołka, który łączy się z tymi samymi krawędziami. | Transformacja grafu a) transformowany wierzchołek b) podgraf skonstruowany na podstawie tego wierzchołka, który łączy się z tymi samymi krawędziami. | ||
}} | }} | ||
| Linia 59: | Linia 59: | ||
</div> | </div> | ||
</div> | </div> | ||
== Zadanie 4 == | == Zadanie 4 == | ||
Wersja z 15:09, 15 wrz 2006
Zadanie 1
Masz dany graf wraz z dwoma wybranymi wierzchołkami . Pokaż jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalną liczbę wierzchołkowo rozłącznych ścieżek z do . Wierzchołki i będą oczywiście wspólne dla tych ścieżek.
Zadanie 2
Masz daną sieć przepływową wraz z dwoma wybranymi wierzchołkami , w której wszystkie przepustowości krawędzi wynoszą 1. Pokaż jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalny przepływ z do w sieci .
Zadanie 3
Masz daną planarną sieć przepływową wraz z dwoma wybranymi wierzchołkami , w której wszystkie przepustowości krawędzi wynoszą . Pokaż jak rozwiązać problem wyznaczenia maksymalnego przepływu w sieci poprzez znalezienie maksymalnego skojarzenia w planarnym grafie dwudzielnym, tzn., pokaż konstrukcje tak ta przedstawiona w Zadaniu 1 i 2, ale zachowującą planarność grafu.
Zadanie 4
Masz dany graf dwudzielny. Pokaż jak używając algorytmu Hopcrofta-Karpa wyznaczyć minimalne pokrycie wierzchołkowe tego grafu.