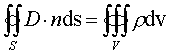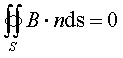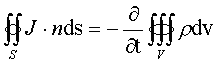TTS Moduł 2

Wykład

---

---

• WPROWADZENIE - WIELKOŚCI CHARAKTERYZUJĄCE POLE EM

Pola elektryczne i magnetyczne kiedy zmieniają się, to powiązane są ze sobą wieloma związkami, nazwanymi wspólnie równaniami Maxwella. Równania te oparte są na wielu fizycznych eksperymentach prowadzonych przez uczonych całe dziesięciolecia. Równania Maxwella pełnią rolę fundamentu dla całej techniki mikrofalowej, tworzonej i rozwijanej przez ostatnie 100 lat.

Równania Maxwella wiążą ze sobą najważniejsze wielkości pola elektromagnetycznego. Zajmiemy się przestrzenią wypełnioną jednorodnym, izotropowym ośrodkiem, charakteryzowanym przez :

• Przenikalność elektryczna ośrodka $\epsilon$ , w próżni równa $\epsilon \equiv {\epsilon }_0=10^{-9}/36\pi [F/m]$ .
• Przenikalność magnetyczna ośrodka $\mu$ , w próżni równa $\mu \equiv {\mu }_0=4\pi \cdot 10^{-7}[H/m]$ .
• Przewodność właściwa ośrodka $\sigma$ (konduktywność), jej miarą jest $[S/m]$, w próżni $\sigma =0$ .

Pole elektromagnetyczne jest kompozycją pól elektrycznego i magnetycznego. Charakteryzują go następujące wielkości:

• Natężenie pola elektrycznego $E(x,y,z,t)$ jest wektorem (ma swoją wartość i kierunek), funkcją miejsca i czasu. Natężenie pola elektrycznego mierzymy w woltach na metr $[V/m]$.
• Natężenie pola magnetycznego $H(x,y,z,t)$ jest także wektorem, mierzymy jego wartość w amperach na metr $[A/m]$.
• Indukcja elektryczna $D=\epsilon E$ jest wektorem, w ośrodku izotropowym skierowanym w tą samą stronę, co natężenie pola elektrycznego, w próżni $D={\epsilon }_{0}E$ , mierzymy jej wartość w amperach razy sekunda na metr kwadratowy $[As/m^2]$, czyli kulombach na metr kwadratowy $[C/m^2]$.
• Indukcja magnetyczna $B=\mu H$ jest wektorem, w ośrodku izotropowym skierowanym w tą samą stronę, co natężenie pola magnetycznego, w próżni $B={\mu }_{0}H$ , mierzymy jej wartość w voltach razy sekunda na metr kwadratowy $[Vs/m^2]$.

• RÓWNANIA MAXWELLA

• Całkowa postać równań Maxwella

Jak powiedziano wyżej, równania Maxwella opierają się odkrytych eksperymentalnie prawach fizycznych.

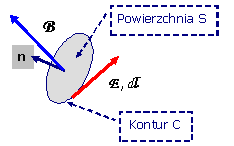
Rys.2.1. Powierzchnia $S$ o konturze $C$ w polu $EM$ o indukcji magnetycznej $B=\mu H$ i natężeniu pola elektrycznego $E$.

Pierwsze prawo Maxwella w postaci całkowej jest zapisem prawa Faradaya. Rozważane są indukcja pola magnetycznego $B=\mu H$ i natężenie pola elektrycznego $E$ w sąsiedztwie powierzchni $S$ otoczonej konturem $C$, co pokazano na rys.2.1.

Pierwsze prawo Maxwella wiąże ze sobą zmianę strumienia indukcji magnetycznej przenikającego powierzchnię $S$ z polem elektrycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię.

${\oint }_{C}Edl=-\underset{S}{\iint }\frac{\partial B}{\partial t}\cdot nds$

(2-1)

Drugie równanie Maxwella w postaci całkowej (2-2) jest zapisem prawa Ampere’a. Wiąże ono ze sobą prąd płynący przez powierzchnię $S$ z polem magnetycznym $H$ , całkowanym wzdłuż zamkniętego konturu $C$.

${\oint }_{C}Hdl=-\underset{S}{\iint }(J+\frac{\partial D}{\partial t})\cdot nds$

(2-2)

Prawo Gaussa zastosowane dla pola elektrycznego mówi, że strumień wektora indukcji pola elektrycznego $D$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ równy jest zgromadzonemu w tej objętości ładunkowi. Ładunek ten otrzymujemy całkując gęstość tego ładunku $\rho$ mierzoną w kulombach na metr sześcienny w objętości $V$ równanie (2-3).

(2-3)

To samo prawo zastosowane do strumienia wektora indukcji pola magnetycznego prowadzi do równanie (1-4),

(2-4)

gdyż pole magnetyczne jest bezźródłowe.

Do powyższych równań dodawane jest zapisane w formie całkowej równanie ciągłości prądu

(2-5)

Mówi ono, że prąd przewodzenia wypływający przez powierzchnię $S$ zamkniętej objętości $V$ równy jest szybkości zmian ładunku w tej objętości.

• Różniczkowa postać równań Maxwella

Równanie Maxwella w postaci całkowej opisują poparte eksperymentami zachowanie rozmaitych wielkości opisujących pole elektromagnetyczne. Ich interpretacja fizyczna jest czytelna.

$\mathrm{\nabla }\times E=-\frac{\partial B}{\partial t}$ $\mathrm{\nabla }\times H=J+\frac{\partial D}{\partial t}$ $\mathrm{\nabla }\cdot J=-\frac{\partial \rho }{\partial t}$ $\mathrm{\nabla }\cdot D=\rho$ $\mathrm{\nabla }\cdot B=0$

(2-6)

Z wielu względów wygodnie jest zapisać te równania w postaci różniczkowej. Otrzymujemy wtedy zestaw równań (2-6).

Pięć powyższych równań podawanych jest tradycyjnie jako równania Maxwella. Z matematycznego punktu widzenia występują związki między nimi, gdyż ostatnie dwa mogą być wyprowadzone w oparciu o pierwsze trzy. Z opisowego punktu widzenia pozostawimy w tym miejscu wszystkie z nich.

• Równanie Maxwella w notacji zespolonej

Przyjmiemy teraz założenie, że natężenia pól elektrycznego i magnetycznego oraz prądy zmieniają się sinusoidalnie w czasie. Pozwala to wprowadzić notację zespoloną. Zespolone wektory $E,D,H,B$ i $J$ związane są z wektorami rzeczywistymi zależnościami w formie (2-7).

$E(x,y,z,t)=Re\{E(x,y,z)exp(j\omega t)\}$

(2-7)

W praktyce takie w przeważającej liczbie przypadków powyższe założenia są spełnione.

Pochodne po czasie wielkości zmiennych sinusoidalnie, czasami mówimy harmonicznie, w czasie obliczamy zgodnie z regułą (2-8):

$\frac{\partial e^{j\omega t}}{\partial t}=j\omega e^{j\omega t}$

(2-8)

Pozwala to zapisać równania Maxwella w innej, uproszczonej formie, w której usunięto zależność występujących w nich zmiennych od czasu. W notacji zespolonej podawane są zwykle tylko cztery z nich.

$\mathrm{\nabla }\times E=-j\omega B$ $\mathrm{\nabla }\times H=J+j\omega D$ $\mathrm{\nabla }\cdot D=\rho$ $\mathrm{\nabla }\cdot B=0$

(2-9)

Dla ośrodka jednorodnego, w którym nie ma ładunków i prądów przewodzenia równania powyższe upraszczają się do postaci (2-10):

$\mathrm{\nabla }\times E=-j\omega B$ $\mathrm{\nabla }\times H=j\omega D$ $\mathrm{\nabla }\cdot D=0$ $\mathrm{\nabla }\cdot B=0$

(2-10)

• POLA W OŚRODKACH I WARUNKI BRZEGOWE

• Rodzaje ośrodków

W poprzednim punkcie założyliśmy, że pola elektryczne i magnetyczne występują w nieograniczonym ośrodku. Dokonajmy przeglądu ośrodków ze względu na własności elektryczne, które określają postać zależności między wektorami $E,D,H,B$ i $J$. W szerokiej klasie ośrodków zależności między tymi wektorami można zapisać w postaci tzw. równań materiałowych

$D=\epsilon E$ $B=\mu H$ $J=\sigma E$

(2-11)

Przypomnijmy, że wartości $\epsilon ,\mu ,\sigma$ charakteryzujące ośrodek to przenikalność elektryczna, przenikalność magnetyczna oraz konduktywność, czyli parametry materiałowe ośrodka.

Związki (2-11) wskazują na liniową zależność wektorów indukcji oraz gęstości prądu od natężeń pól. Oznacza to, że wielkości $\epsilon ,\mu ,\sigma$ nie zależą od natężeń pól i taki ośrodek nazywamy liniowym. Jeżeli przynajmniej jeden z parametrów ośrodka zależy od natężeń pól, to zależności (2-11) nie są już liniowe i ośrodek nazywa się nieliniowym.

Ośrodek jest jednorodny gdy jego parametry nie zależą od współrzędnych punktu. W przeciwnym przypadku mówimy o ośrodku niejednorodnym.

Istnieją ośrodki, których parametry $\epsilon ,\mu ,\sigma$ zależą od częstotliwości. Ośrodki takie nazywamy dyspersyjnymi. Równania materiałowe w formie (2-11) mają sens dla ośrodków dyspersyjnych tylko w przypadku sinusoidalnej zależności pól od czasu. Dla dowolnej zależności pól od czasu związki (2-11) są słuszne dla transformat fourierowskich wektorów $E,D,H,B,J$.

Jeżeli wielkości $\epsilon ,\mu ,\sigma$ są niezależne od kierunku pól, to parametry te są skalarami, a taki ośrodek nazywamy izotropowym. Odpowiednie wektory występujące w poszczególnych równaniach (2-11) są do siebie równoległe.

Gdy parametry ośrodka zależą od kierunku pól, to mówimy o ośrodku anizotropowym, którego własności nie mogą być opisane przez skalarne wielkości $\epsilon ,\mu ,\sigma$. Równania (2-11) mogą być prawdziwe dla ośrodka anizotropowego, ale wtedy parametry materiałowe są reprezentowane przez tensory. Przykładowo, gdy związek między wektorami $E$ i $D$ zależy od kierunku wektora $E$ to przenikalność elektryczna jest tensorem, $[\epsilon ]$, reprezentowanym przez 9-elementową macierz, a relacja między wektorami $D$ i $E$ przybiera postać

$\left[\begin{array}{c}{D}_x\\ D_y\\ D_z\end{array}\right]=\left[\begin{array}{ccc}{\epsilon }_{xx}& {\epsilon }_{xy}& {\epsilon }_{xz}\\ {\epsilon }_{yx}& {\epsilon }_{yy}& {\epsilon }_{yz}\\ {\epsilon }_{zx}& {\epsilon }_{zy}& {\epsilon }_{zz}\end{array}\right]\left[\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right]$

(2-12)

Z powyższego równania wynika, że jedna składowa wektora pola elektrycznego wywołuje, w ogólności, trzy składowe wektora indukcji elektrycznej.

Struktury krystaliczne, np. półprzewodniki, oraz zjonizowane gazy są przykładami anizotropowych dielektryków.

Analogiczną do (2-12) relację można określić dla związku między wektorami $B$ i $H$, w którym przenikalność magnetyczna jest tensorem. W technice mikrofalowej stosuje się ferryty, które są anizotropowymi materiałami magnetycznymi.

• Dielektryki

Materiały dielektryczne powszechnie występują w technice mikrofalowej w konstrukcji tak linii transmisyjnych jak i elementów oraz podzespołów. Rozważmy zachowanie izotropowego dielektryka w zewnętrznym polu elektrycznym o sinusoidalnej zależności od czasu, stosując wektory zespolone.

Pod wpływem pola elektrycznego cząsteczki materii ustawiają się zgodnie z prawem Coulomba tak, że wywołują własne pole elektryczne skierowane przeciwnie do pola zewnętrznego. Zjawisko to określamy mianem elektrycznej polaryzacji (lub krótko polaryzacją) ośrodka i opisujemy przez wektor polaryzacji $P_e$. Wektory $P_e$, $E$ i $D$ powiązane są ze sobą zależnością

$D={\epsilon }_{0}E+P_e$

(2-13)

W ośrodku liniowym, polaryzacja elektryczna jest liniowo związana z zewnętrznym polem elektrycznym jako

$P_e={\epsilon }_0{\chi }_{e}E$

(2-14)

przy czym ${\chi }_e$, która może być zespolona, nazywa się podatnością elektryczną. Tak więc:

$D={\epsilon }_{0}E+P_e={\epsilon }_0(1+{\chi }_e)E=\epsilon E$

(2-15)

gdzie:

$\epsilon ={\epsilon }_0(1+{\chi }_e)={\epsilon }^{\prime }-j{\epsilon }^{″}$

(2-16)

jest zespoloną przenikalnością elektryczną ośrodka.

Zespolony zapis dla przenikalności elektrycznej (2-16) może być stosowany tylko w przypadku pól o sinusoidalnej zależności od czasu.

Przenikalność elektryczną znormalizowaną względem przenikalności elektrycznej próżni nazywamy zespolona względną przenikalnością elektryczną:

${\epsilon }_w=\frac{\epsilon }{{\epsilon }_0}=1+{\chi }_e={\epsilon }_w^{\text{'}}-j{\epsilon }_w^{{\text{'}}^{\prime }}$

(2-17)

W przypadku statycznym lub przy wolnych zmianach pola wektor polaryzacji elektrycznej jest w przybliżeniu w fazie z wektorem pola elektrycznego. Dla pól szybkozmiennych opóźnienie wektora $P_e$ względem wektora $E$ nie jest pomijalnie małe, wymienione wektory mają różne fazy. Część urojona $\epsilon$, która opisuje straty w ośrodku (grzanie) wywołane tłumieniem wibracji dipoli i tym samym opóźnienie wektora polaryzacji względem wektora pola elektrycznego, musi być ujemna (${\epsilon }^{″}$ jest dodatnie).

Źródłem strat w dielektryku może być również niezerowa konduktywność ośrodka i wtedy istnieje w ośrodku wektor gęstości prądu przewodzenia opisany zależnością:

$J=\sigma E$

(2-18)

która jest prawem Ohma z punktu widzenia pola elektromagnetycznego.

Całkowita gęstość prądu (przewodzenia i przesunięcia) w dielektryku, która występuje po prawej stronie drugiego równania Maxwella (2-19), wynosi

$\begin{array}{ccc}{J}_C& =& J+j\omega \epsilon E=\sigma E+j\omega ({\epsilon }^{\prime }-j{\epsilon }^{″})E\\ & =& j\omega {\epsilon }^{\prime }E+(\sigma +\omega {\sigma }^{″})E=j\omega [{\epsilon }^{\prime }-j({\epsilon }^{″}+\frac{\sigma }{\omega }\left)\right]E\end{array}$

(2-19)

Z zależności (2-17) wynika, że straty wynikające z tłumienia oscylacji dipoli ($\omega {\epsilon }^{″}$) i straty wynikające z istnienia prądu przewodzenia ($\sigma$) są nierozróżnialne. Wielkość $\sigma +\omega {\epsilon }^{″}$ można traktować jako zastępczą konduktywność ośrodka. Z kolei wielkość ${\epsilon }^{″}+\sigma /\omega$ można określić jako zastępczą część urojoną przenikalności elektrycznej.

Stratność dielektryka możemy charakteryzować przez podanie tangensa kąta stratności wyrażonego wzorem

$tg{\delta }_{\epsilon }=\frac{\sigma +\omega {\epsilon }^{″}}{\omega {\epsilon }^{\prime }}$

(2-20)

który jest stosunkiem składowej prądu będącego w fazie z polem elektrycznym (ten prąd wywołuje straty mocy fali elektromagnetycznej w ośrodku) do składowej prądu proporcjonalnej do $\omega {\epsilon }^{\prime }$, odpowiedzialnej za magazynowanie energii pola elektrycznego.

Zwykle dielektryki charakteryzuje się podając stałą dielektryczną, która jest rzeczywistą częścią względnej przenikalności elektrycznej, oznaczaną w literaturze najczęściej jako ${\epsilon }_w$ (z pominięciem indeksu „’ ”, co może wprawiać w zakłopotanie) oraz tangensa kąta stratności dla określonej częstotliwości.

• Magnetyki

Dla izotropowych magnetyków można zastosować podobny opis jak dla dielektryków. Zewnętrzne pole magnetyczne porządkuje magnetyczne dipole w materiale wywołując wektor magnetyzacji ośrodka opisany wektorem $P_m$ związanym w ośrodku liniowym z zewnętrznym polem magnetycznym zależnością

$P_m={\mu }_0{\chi }_{m}H$

(2-21)

gdzie zespolona wielkość ${\chi }_m$ nazywa się podatnością magnetyczną.

$B={\mu }_{0}H+P_m={\mu }_0(1+{\chi }_m)H=\mu H$

(2-22)

gdzie

$\mu ={\mu }_0(1+{\chi }_m)={\mu }^{\prime }j{\mu }^{″}$

(2-23)

jest zespoloną przenikalnością magnetyczną ośrodka.

Przenikalność magnetyczną znormalizowaną względem przenikalności magnetycznej próżni nazywamy zespolona względną przenikalnością magnetyczną:

${\mu }_w=\frac{\mu }{{\mu }_0}=1+{\chi }_m={\mu }_w^{\text{'}}-j{\mu }_w^{{\text{'}}^{\prime }}$

(2-24)

Analogicznie jak dla dielektryków, część urojona $\mu$ lub ${\chi }_m$ opisuje straty w magnetyku wywołane tłumieniem wibracji dipoli magnetycznych i wektor polaryzacji magnetycznej jest opóźniony względem wektora pola magnetycznego. W przypadku ośrodków magnetycznych nie ma magnetycznej konduktancji, ponieważ nie ma magnetycznego prądu przewodzenia.

Przy analizie własności ośrodków magnetycznych uwzględnia się straty magnetyczne wprowadzając, analogicznie jak poprzednio, tangens kąta stratności

$tg{\delta }_m=\frac{{\mu }^{″}}{{\mu }^{\prime }}$

(2-25)

Tak więc ośrodki magnetyczne możemy opisać podając część rzeczywistą przenikalności magnetycznej oraz tangens kąta stratności.

Równania Maxwella w formie różniczkowej (2-9) wymagają znajomości wartości brzegowych, aby uzyskać jednoznaczne rozwiązanie w danym ośrodku.

• Warunki brzegowe dla pola EM

W wielu zagadnieniach występujących w technice mikrofalowej mamy do czynienia z układem dwóch dielektryków bądź ze strukturą dielektryk – przewodnik. Rozważmy zachowanie pola elektromagnetycznego w tych szczególnych przypadkach.

Na granicy miedzy dwoma dielektrykami zwykle nie występuje ładunek powierzchniowy oraz nie płynie prąd przewodzenia. Dokładne wyprowadzenia prowadzą do wniosku, że składowe normalne wektorów $D$ i $B$ oraz składowe styczne wektorów $E$ i $H$ są ciągłe na granicy dielektryków. Przyjmując, że składowa normalna jest równoległa do jednej osi w trójwymiarowym układzie współrzędnych to powyższe warunki określają zachowanie sześciu składowych pola elektromagnetycznego (składowa styczna składa się z dwóch składowych). Można wykazać, że spełnienie warunków brzegowych dla składowych stycznych na granicy dwóch ośrodków dielektrycznych pociąga za sobą automatycznie spełnienie warunków ciągłości dla składowych normalnych.

W liniach transmisyjnych powszechnie występuje granica między dielektrykiem i dobrym przewodnikiem, który często można uznać za idealny. Warunki brzegowe dla pól zmiennych w czasie panujące na granicy dielektryka i idealnego przewodnika zapisuje się następująco:

$n\times E_2=0$

(2-26)

$n\times H_2=J_s$

(2-27)

$n\cdot D_2={\rho }_s$

(2-28)

$n\cdot B_2=0$

(2-29)

W idealnym przewodniku pole elektryczne musi być równe zeru, gdyż w przeciwnym przypadku wywoływałoby prąd przewodzenia o nieskończonym natężeniu. Istnienie w tym ośrodku zmiennego pola magnetycznego jest również niemożliwe, ponieważ zgodnie z pierwszym prawem Maxwella musiałoby wywołać pole elektryczne, co byłoby sprzeczne z poprzednim stwierdzeniem.

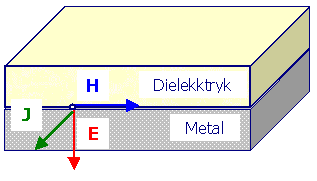
Rys.2.4. Pola i prąd powierzchniowy na granicy metalu i dielektryka

W rezultacie dochodzimy do wniosku, że składowa styczna pola elektrycznego na granicy idealnego przewodnika jest równa zeru, a więc pole elektryczne musi być prostopadłe do powierzchni przewodnika. Pole elektryczne indukuje na powierzchni przewodnika powierzchniowy ładunek elektryczny o gęstości równej wartości indukcji elektrycznej. Składowa normalna indukcji magnetycznej jest zerowa na brzegu idealnego przewodnika, czyli pole magnetyczne musi być styczne do granicy przewodnika i wywołuje na jego powierzchni prąd przewodzenia o gęstości równej wartości natężenia pola magnetycznego.

• RÓWNANIA FALOWE W DIELEKTRYKU

• Równania falowe w dielektryku bezstratnym

Rozważamy przestrzeń nieograniczoną wypełnioną ośrodkiem liniowym, izotropowym, niedyspersyjnym, jednorodnym i bezstratnym. Zakładamy, że w ośrodku nie ma prądów i ładunków co oznacza, że wszelkie źródła pól są nieskończenie daleko od rozważanego obszaru.

Parametry ośrodka $\epsilon$ i $\mu$ są liczbami stałymi i układ równań Maxwella (2-6) sprowadza się do czterech następujących zależności

$\mathrm{\nabla }\times E=-\mu \frac{\partial H}{\partial t}$ $\mathrm{\nabla }\times H=\epsilon \frac{\partial E}{\partial t}$ $\mathrm{\nabla }\cdot E=0$ $\mathrm{\nabla }\cdot H=0$

(2-30)

W celu rozwiązania układu równań (2-30), poddajemy pierwsze równanie układu obustronnie rotacji i wstawiamy do uzyskanej zależności drugie z równań (2-30), tak więc

$\mathrm{\nabla }\times \mathrm{\nabla }\times E=-\mu \frac{\partial }{\partial t}\mathrm{\nabla }\times H=-\mu \epsilon \frac{{\partial }^{2}E}{\partial t^2}$

(2-31)

Lewą stronę równania (1-31) przekształcamy zgodnie z poniższą tożsamością wektorową

$\mathrm{\nabla }\times \mathrm{\nabla }\times E=\mathrm{\nabla }(\mathrm{\nabla }\cdot E)-{\mathrm{\nabla }}^{2}E$

(2-32)

i uwzględniamy to, że dywergencja pola $E$ jest równa zeru (trzecie równanie w układzie (2-30)). W wyniku uzyskujemy równanie falowe dla pola elektrycznego:

${\mathrm{\nabla }}^{2}E-\mu \epsilon \frac{{\partial }^{2}E}{\partial t^2}=0$

(2-33)

Podobnie, eliminując z układu równań Maxwella wektor $E$, otrzymujemy równanie falowe spełniane przez wektor pola magnetycznego. Postać tego równania jest analogiczna do równania (2-33).

${\mathrm{\nabla }}^{2}H-\mu \epsilon \frac{{\partial }^{2}H}{\partial t^2}=0$

(2-34)

Należy zaznaczyć, że układ równań Maxwella nie jest równoważny układowi równań falowych. Równania falowe wynikają z równań Maxwella, ale wynikanie odwrotne nie zachodzi. Z tego względu każde rozwiązanie układu równań Maxwella musi spełniać równania falowe, a wśród wektorów spełniających równania falowe mogą być takie, które nie są rozwiązaniami układu równań Maxwella.

Analiza rozwiązania powyższych równań falowych prowadzi do wniosku, że prędkość $\nu$ rozchodzenia się zaburzenia w przestrzeni określona jest iloczynem $\mu \epsilon$ , gdyż $\nu =1/\sqrt{\mu \epsilon }$ .

W próżni jest to prędkość światła $\nu \equiv c=1/\sqrt{{\mu }_0{\epsilon }_0}$ .

• Równania falowe w dielektryku stratnym

Utrzymajmy w mocy wszystkie założenia dotyczące ośrodka wypełniającego przestrzeń (liniowość, izotropowość, jednorodność), ale przyjmijmy, że straty występujące w ośrodku opisuje konduktywność $\sigma$ różna od zera. W tym przypadku układ równań Maxwella przyjmuje postać

$\mathrm{\nabla }\times E=-\mu \frac{\partial H}{\partial t}$ $\mathrm{\nabla }\times H=\sigma E+\epsilon \frac{\partial E}{\partial t}$ $\mathrm{\nabla }\cdot E=0$ $\mathrm{\nabla }\cdot H=0$

(2-35)

Przekształcając równania Maxwella, metodami analogicznymi do stosowanych w poprzednim punkcie, można uzyskać równania falowe dla ośrodka stratnego

${\mathrm{\nabla }}^2\times E-\mu \epsilon \frac{\partial E}{\partial t}-\mu \epsilon \frac{{\partial }^{2}E}{\partial t^2}=0$ ${\mathrm{\nabla }}^2\times H-\mu \epsilon \frac{\partial H}{\partial t}-\mu \epsilon \frac{{\partial }^{2}H}{\partial t^2}=0$

(2-36)

Rozwiązanie tych równań w przypadku dowolnej zależności pól od czasu jest skomplikowane i nie prowadzi do tak prostej interpretacji fizycznej i geometrycznej jak w przypadku ośrodków bezstratnych. Celowym jest przyjęcie, że pola tworzące fale elektromagnetyczną są cosinusoidalnymi funkcjami czasu o ustalonej pulsacji i zastosowanie rachunku zespolonego (w dziedzinie częstotliwości).

• Równania falowe w dielektryku stratnym w notacji zespolonej

Przekształcając równania falowe (2-36) do postaci zespolonej uzyskujemy następujące równania falowe w dziedzinie zespolonej (równania Helmholtza):

${\mathrm{\nabla }}^{2}E-{\gamma }^{2}E=0$ ${\mathrm{\nabla }}^{2}H-{\gamma }^{2}H=0$

(2-37)

W równaniach pojawia się zmienna zespolona $\gamma$ zwana współczynnikiem propagacji, o fundamentalnym znaczeniu dla opisu zjawiska propagacji fali

${\gamma }^2=j\omega \mu (\sigma +j\omega \epsilon )$

(2-38)

Pamiętamy, że współczynnik propagacji fali w nieograniczonym ośrodku określają wielkości charakteryzujące ten ośrodek.

• FALA PŁASKA

• Pola fali płaskiej

Fala wypromieniowana przez antenę nadawczą rozchodzi się we wszystkich kierunkach, choć oczywiście pewne kierunki są uprzywilejowane, o czym mówi charakterystyka anteny. Z punktu widzenia anteny odbiorczej oddalonej odpowiednio daleko, o wiele kilometrów, fala dochodząca do niej jest falą płaską. Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Na podstawie równania falowego możemy znaleźć matematyczny opis takiej fali.

Rozważamy przypadek, w którym składowe pola są harmonicznymi funkcjami czasu. Wykorzystujemy równania Helmholtza w postaci (2-37). Możemy je zapisać w kartezjańskim układzie współrzędnych w formie (2-39):

$\frac{{\partial }^{2}E}{\partial x^2}+\frac{{\partial }^{2}E}{\partial y^2}+\frac{{\partial }^{2}E}{\partial z^2}-{\gamma }^{2}E=0$ $\frac{{\partial }^{2}H}{\partial x^2}+\frac{{\partial }^{2}H}{\partial y^2}+\frac{{\partial }^{2}H}{\partial z^2}-{\gamma }^{2}H=0$

(2-39)

Pierwsze równanie musi być spełnione dla każdej ze składowych $E_x,E_y$ i $E_z$ pola elektrycznego, a drugie dla analogicznych składowych pola magnetycznego.

Stwierdzamy, nie wdając się w matematyczne uzasadnienia, że dla fali płaskiej natężenie pola elektrycznego $E$ i magnetycznego $H$ są wektorami poprzecznymi ET i HT do kierunku propagacji, i mówimy, że fala płaska jest falą poprzeczną czyli typu TEM (ang. Transverse Electro- Magnetic).

Przyjmijmy, że fala rozchodzi się wzdłuż osi $z$. Wektory $E_T$ i $H_T$ leżą w płaszczyźnie $xy$ i są niezależne od współrzędnych $x$ i $y$, co oznacza

$\frac{\partial E_T}{\partial x}=\frac{\partial E_T}{\partial y}=0;\frac{\partial H_T}{\partial x}=\frac{\partial H_T}{\partial y}=0$

(2-40)

Pamiętajmy, że dla omawianego przypadku

$E_T=i_x{E}_x+i_y{E}_y;H_T=i_x{H}_x+i_y{H}_y$

(2-41)

Równania (2-39) upraszczają się do

$\frac{{\partial }^2{E}_T}{\partial z^2}-{\gamma }^2{E}_T=0$ $\frac{{\partial }^2{H}_T}{\partial z^2}-{\gamma }^2{H}_T=0$

(2-42)

Rozwiązania równań (1-42) mają prostą dwuczłonową postać (2-43):

$E_T(z)=E_{T0}^{+}{e}^{-\gamma z}+E_{T0}^{-}{e}^{\gamma z}$ $H_T(z)=H_{T0}^{+}{e}^{-\gamma z}+H_{T0}^{-}{e}^{\gamma z}$

(2-43)

Obecność dwóch członów w rozwiązaniach, to dwie fale rozchodzące się wzdłuż osi z:

• fala postępująca propagowana zgodnie z kierunkiem osi z o czym informuje czynnik Parser nie mógł rozpoznać (błąd składni): {\displaystyle e^{-\gamma z\,} ;
• fala powracająca rozchodzi się w kierunku przeciwnym do osi z co opisuje Parser nie mógł rozpoznać (błąd składni): {\displaystyle e^{\gamma z\,} .

Przyjmijmy, że mamy tylko falę postępującą. Gdy znamy jeden z wektorów fali płaskiej, pola elektrycznego albo pola magnetycznego, to drugi możemy wyznaczyć posługując się zależnościami:

$E_T=Z_f{H}_f\times i_z$ $H_T=\frac{1}{Z_f}{i}_z\times E_T$

(2-44)

Współczynnik występujący w pierwszym z równań (2-44) zdefiniowany jako stosunek wartości wzajemnie prostopadłych (prostopadłych do kierunku rozchodzenia się fali) składowych pola elektrycznego i magnetycznego nazywamy impedancją falową

$Z_f=\frac{E_T}{H_T}=\frac{E_x}{H_y}=-\frac{E_y}{H_x}$

(2-45)

Dla fali płaskiej impedancja falowa jest dana zależnością

$Z_f=\sqrt{\frac{j\omega \mu }{\sigma +j\omega \epsilon }}$

(2-46)

Równocześnie wielkość zespolona zdefiniowana wzorem

$Z_w=\sqrt{\frac{j\omega \mu }{\sigma +j\omega \epsilon }}$

(2-47)

ma wymiar impedancji, zależy od parametrów ośrodka oraz pulsacji i nazywa się impedancją właściwą ośrodka. Dla ośrodka bezstratnego impedancja właściwa jest rzeczywista, zależy tylko od parametrów ośrodka i dla próżni równa jest

$Z_{w0}=\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}=120\pi [\mathrm{\Omega }]$ .

(2-48)

Jak wynika z równości (2-46) oraz (2-47), w przypadku fali typu TEM w nieograniczonej przestrzeni impedancja falowa jest równa impedancji właściwej ośrodka. Cecha ta nie jest własnością wszystkich fal elektromagnetycznych, a jedynie fal typu TEM.

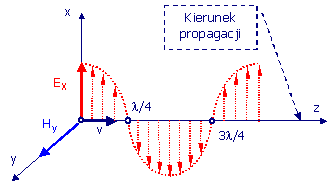
Rys.2.5. Składowe pola elektrycznego i magnetycznego fali płaskiej w ośrodku bezstratnym.

Ze zależności (2-44) wynika, że wektory natężenia pól elektrycznego i magnetycznego są do siebie prostopadłe oraz, że trójka wektorów $E_T$, $H_T$, iz jest prawoskrętna. Własność tę mają na ogół tylko fale w ośrodkach nieograniczonych i izotropowych.

Gdy położenie osi $x$ zostanie tak dobrane, by pole elektryczne miało tylko składową $H_T=H_y$, to wtedy pole magnetyczne ma jedynie składową $E_T=E_x$ (zgodnie z równaniami (2-44)). Przykład pól elektrycznego i magnetycznego takiej fali płaskiej ilustruje rys.2.5.

Dla fali rozchodzącej się w ośrodku izotropowym o parametrach $\epsilon ,\mu ,\sigma$ zgodnie z kierunkiem osi z mającej tylko składową $E_x$, której wartość jest równa liczbie rzeczywistej $E_0$ w płaszczyźnie $z=0$, pola zapiszemy w dziedzinie zespolone następująco

$E_x(z)=E_0{e}^{-\gamma z}$

(2-49a)

$H_y(z)=\frac{E_0}{|Z_w|}{e}^{-j\phi }{e}^{-\gamma z}=H_0{e}^{-j\phi }{e}^{-\gamma z}$

(2-49b)

gdzie impedancję właściwą zapisano w postaci wykładniczej $Z_w=|Z_w|e^{j\phi }$. Współczynnik propagacji $\gamma$, zwany niekiedy stałą propagacji, został opisany równaniem (2-38). W ogólnym przypadku $\gamma$ jest liczbą zespoloną:

$\gamma =\alpha +j\beta$

(2-50)

Część rzeczywistą współczynnika propagacji $\alpha$ nazywamy stałą tłumienia, a część urojoną $\beta$ jest stałą fazową i w ośrodku stratnym

$\alpha =Re\{\sqrt{j\omega \mu (\sigma +j\omega \epsilon )}\}$

(2-51a)

$\beta =Im\{\sqrt{j\omega \mu (\sigma +j\omega \epsilon )}\}=Im\left\{j\omega \sqrt{\mu \epsilon }\sqrt{1+\frac{\sigma }{j\omega \epsilon }}\right\}$

(2-51b)

W próżni, gdy przewodność ośrodka $\sigma =0$ a $\epsilon ={\epsilon }_0$ i $\mu ={\mu }_0,\gamma$ jest czysto urojone.

${\gamma }^2=-{\omega }^2{\epsilon }_0{\mu }_0$

(2-52a)

$\beta =\omega \sqrt{{\epsilon }_0{\mu }_0}$

(2-52b)

Korzystając z definicji (2-50) zależności (2-49) przybierają postać

$E_x(z)=E_0{e}^{-\alpha z}{e}^{-j\beta z}$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle \displaystyle H_y(z)=H_0 e^{-\alpha z }e^{-j(\beta z +\varphi)}

(2-53)

Jak wiemy przejście od notacji zespolonej do rzeczywistej jest proste:

$E_x(z,t)=Re\{E_0{e}^{-\alpha z}{e}^{-j\beta z}{e}^{j\omega t}\}=E_0{e}^{-\alpha z}cos(\omega t-\beta z)$

(2-54a)

$H_y(z,t)=Re\{H_0{e}^{-\alpha z}{e}^{-j(\beta z+\phi )}{e}^{j\omega t}\}=H_0{e}^{-\alpha z}cos(\omega t-\beta z-\phi )$

(2-54b)

Z zapisu pól podanych w (1-54) widać, że stała tłumienia wpływa jedynie na zmniejszanie się amplitudy danego pola, a stała fazowa informuje o tempie zmiany fazy fali wzdłuż osi z. Gdy fala rozchodzi się w ośrodku bezstratnym amplitudy pól nie zmniejszają i pole elektryczne jest w fazie z polem magnetycznym ($\phi =0$).

Prędkość fazową fali płaskiej znajdujemy analizując ruch płaszczyzny stałej fazy. Dla tej płaszczyzny spełniony jest warunek (2-55):

$\omega t-\beta z=const.$

(2-55)

Płaszczyzna ta porusza się z prędkością $v_f$:

$v_f=\frac{\omega }{\beta }$

(2-56)

Zwróćmy uwagę, że stała fazowa dla fali propagowanej w ośrodku stratnym opisana relacją (1-51b) nie jest liniową funkcją $\omega$ i prędkość fazowa zmienia się z częstotliwością. Mówimy wtedy o dyspersji fali, która w tym wypadku wynika ze strat ośrodka.

Dla próżni prędkość fazowa fali równa jest prędkości $c$ światła:

$v_f=c=\frac{1}{{\epsilon }_0{\mu }_0}$

(2-57)

Droga, jaką fala poruszająca się prędkością opisaną zależnością (1-56) przebędzie w czasie okresu $T$, nazywa się długością fali $\lambda$.

$\lambda =\frac{\omega T}{\beta }=\frac{2\pi }{\beta }$

(2-58)

Zależność (2-56) podaje wartość prędkości fazowej, ale pamiętajmy, że prędkość jest wielkością wektorową i jej zwrot jest zgodny z wektorem określającym kierunek rozchodzenia się fali. Należy podkreślić, że ruch płaszczyzny stałej fazy jest pojęciem matematycznym i nie oznacza przesuwania się żadnego obiektu materialnego, a tym samym przenoszenia energii. Z tego względu prędkość fazowa może przyjmować dowolne wartości dodatnie i nie podlega ograniczeniom wynikającym ze szczególnej teorii względności.

Aby za pomocą fali EM przesłać informację, trzeba przebieg o pulsacji nośnej $\omega$ zmodulować odpowiednim sygnałem. W wyniku modulacji z sygnału monochromatycznego otrzymujemy widmo częstotliwości. W najprostszym przypadku modulacji amplitudowej jedną częstotliwością otrzymujemy dwie częstotliwości prążków bocznych, różniące się od nośnej o $\mathrm{\Delta }\omega$. Superpozycję kilku fal o zbliżonych częstotliwościach, $\mathrm{\Delta }\omega \to 0$, i współczynnikach fazowych, $\mathrm{\Delta }\beta \to 0$, zwana jest fizyce grupą fal.

Obserwując ruch płaszczyzny stałej fazy obwiedni (np. płaszczyzny, w której superpozycja dwóch fal osiąga maksimum) można zapisać warunek (2-59):

$\mathrm{\Delta }\omega t-\mathrm{\Delta }\beta z=const.$

(2-59)

Prędkość grupowa $v_g$ to prędkość poruszania się obwiedni sygnału:

$v_g=\frac{d\omega }{d\beta }$

(2-60)

Można wykazać, że w ośrodku izotropowym związek pomiędzy prędkością grupową i fazową przybiera postać:

$v_g=\frac{v_f}{1-\frac{\omega }{v_f}\frac{d{v}_f}{d\omega }}$

(2-61)

Ze związku (2-61) wynika, że dla fali, której prędkość fazowa nie zależy od częstotliwości, prędkość grupowa jest równa prędkości fazowej.

• RODZAJE FAL EM W PROWADNICACH FALOWYCH

Do tej pory zajmowaliśmy się falą płaską rozchodzącą się w nieograniczonej przestrzeni, która jest ważnym rodzajem fali elektromagnetycznej w dziedzinie zastosowań telekomunikacyjnych bo występuje pomiędzy antenami nadawczą i odbiorczą.

Niemniej istotne jest rozchodzenie się fal elektromagnetycznych we wszelkiego rodzaju liniach transmisyjnych, w których fale prowadzone są w określonym kierunku. Linie te nazywamy prowadnicami falowymi. Prowadzenie fal uzyskuje się wzdłuż określonego układu przewodników lub dielektryków (tzn. w obszarach cylindrycznych, których granicę są przewodzące lub są to granice dwóch dielektryków, ewentualnie odpowiednia kombinacja wymienionych materiałów). W przypadku prowadzenia fal wzdłuż przewodników, możliwe jest rozchodzenie się energii elektromagnetycznej w liniach składających się z dwóch lub więcej przewodów, a także w rurach (najczęściej o przekroju prostokątnym albo kołowym) nie zawierających wewnątrz dodatkowych przewodników, tzw. falowodach. Natomiast przykładem prowadnicy falowej będącej układem warstw dielektrycznych jest światłowód, bez którego trudno wyobrazić sobie dzisiejszą telekomunikację.

Określenie postaci fali elektromagnetycznej w prowadnicy falowej wiąże się z poszukiwaniem rozwiązań równań Maxwella, które jest zagadnieniem matematycznym innego typu niż w przypadku fali w nieograniczonej przestrzeni. Ze względu na to, że mamy tu do czynienia z obszarem cylindrycznym o granicy przewodzącej lub w formie granicy dwóch dielektryków, musimy teraz uwzględnić warunki brzegowe. Dlatego własności fal elektromagnetycznych w prowadnicach są inne niż dla fali płaskiej.

Okazuje się, że fale w prowadnicach falowych nie muszą być falami typu TEM, tzn. mogą one mieć składowe pól elektrycznego i magnetycznego wzdłuż kierunku rozchodzenia się fali. Wprowadzić należy klasyfikację możliwych rodzajów fal nazywanych również modami.

Przyjmijmy, że fala rozchodzi się zgodnie z kierunkiem osi $z$ i wtedy wyróżnia się następujące typy fal:

Tabela 1.1. Zestawienie właściwości typów fal.

Typ fali	Właściwości pola E i H
Fala typu TEM	$E_z=0$ – pole elektryczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali, Hz=0 – pole magnetyczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali;
Fala typu TM (zwana też E)	$E_z\ne 0$, Hz=0 – pole magnetyczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali;
Fala typu TE (zwana też H)	$H_z\ne 0$, Ez=0 – pole elektryczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali;
Fala typu EH	$E_z\ne 0$,, $H_z\ne 0$,

Z powyższego wykazu wynika, że tylko pierwszy z wymienionych typów fal jest falą poprzeczną. Prowadnice falowe, w których mogą rozchodzić się rodzaje TEM nazywamy liniami TEM lub prowadnicami TEM. Struktura prowadnicy TEM musi zawierać co najmniej dwa przewody. Przykładem linii TEM jest linia współosiowa, tzw. kabel koncentryczny.

Fale E i H rozchodzą się w falowodach. Falowody stosuje się do prowadzenia fali elektro-magnetycznej z mniejszymi stratami niż w linii TEM (np. w transponderach satelitów telekomunikacyjnych) lub do przesyłania dużych mocy, których przesłanie nie jest możliwe linią współosiową (np. w radarach).

Fale typu EH występują między innymi w falowodach dielektrycznych i światłowodach.

Słownik

• Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
• Mikrofale - zakres częstotliwości fal elektromagnetycznych od 300 MHz do 1000 GHz.
• Równania Maxwella - fundamentalne równania techniki mikrofalowej opisujące pole elektromagnetyczne w czasie i przestrzeni.
• Przenikalność dielektryczna $\epsilon$ i magnetyczna $\mu$ -Podstawowe parametry opisujące właściwości przestrzeni odpowiednio dla pola elektrycznego i magnetycznego.
• Podstawowe parametry pola elektromagnetycznego:
  • Natężenie pola elektrycznego $[V/m]$ .
  • Natężenie pola magnetycznego $[A/m]$ .
• Indukcja pola elektrycznego $D$ - wielkość wektorowa proporcjonalna do natężenia pola elektrycznego i przenikalności dielektrycznej.
• Indukcja pola magnetycznego $B$ - wielkość wektorowa proporcjonalna do natężenia pola magnetycznego i przenikalności magnetycznej.
• I prawo Maxwella - z pierwszego równania Maxwella widać że zmienne pole magnetyczne jest źródłem zmiennego pola elektrycznego
  • W postaci całkowej jest zapisem prawa Faradaya i wiąże ze sobą zmianę strumienia indukcji magnetycznej przenikającego powierzchnię $S$ z polem elektrycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię (zal. 2-1).
  • W postaci różniczkowej I prawo Maxwella mówi, że rotacja pola elektrycznego jest równa pochodnej indukcji magnetycznej po czasie (zal.2-6).
• II prawo Maxwella - z drugiego równania Maxwella widać że źródłem zmiennego pola magnetycznego jest zmienny w czasie prąd lub zmienne pole elektryczne.
  • W postaci całkowej jest zapisem prawa Ampera i wiąże ze sobą zmianę strumienia indukcji elektrycznej i prąd przenikający powierzchnię $S$ z polem magnetycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię (zal. 2-2).
  • W postaci różniczkowej II prawo Maxwella mówi nam że rotacja pola magnetycznego jest równa pochodnej indukcji elektrycznej i prądu po czasie (zal.2-6).
• III prawo Maxwella - jest zapisem prawa Gaussa dla pola elektrycznego i mówi, że źródłem pola indukcji elektrycznej są ładunki elektryczne.
  • W postaci całkowej prawo to mówi że strumień wektora indukcji pola elektrycznego $D$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ równy jest zgromadzonemu w tej objętości ładunkowi (zal 2-3).
  • W postaci różniczkowej prawo to mówi że divergencja (rozbieżność) wektora indukcji elektrycznej jest równa gęstości ładunku elektrycznego (zal.2-6).
• IV prawo Maxwella - jest zapisem prawa Gaussa dla pola magnetycznego i mówi, że pole magnetyczne jest bezźródłowe.
  • W postaci całkowej prawo to mówi że strumień wektora indukcji pola magnetycznego $B$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ jest równy 0 co znaczy że pole magnetyczne jest bezźródłowe (zal. 2-4).
  • W postaci różniczkowej prawo to mówi, że divergencja (rozbieżność) wektora indukcji magnetycznej jest równa 0, co również znaczy że pola magnetyczne jest bezźródłowe (zal1-6).
• Równanie ciągłości prądu - opisuje relacje między prądem i ładunkiem elektrycznym.
  • W postaci całkowej prawo to mówi nam, że prąd przewodzenia wypływający przez powierzchnię $S$ zamkniętej objętości V równy jest szybkości zmian ładunku w tej objętości (zal.2-5).
  • W postaci różniczkowej prawo to mówi nam, że źródłem pola gęstości prądów jest zmiana gęstości ładunku w czasie (zal 2-6).
• Parametry materiałowe ośrodka dla pola elektromagnetycznego:
  • Przenikalność dielektryczna $\epsilon$ - określa relację między natężeniem pola elektrycznego a jego indukcją (zal. 2-11)
  • Przenikalność magnetyczna $\mu$ - określa relację między natężeniem pola magnetycznego a jego indukcją (zal. 2-11)
  • Konduktywność $\sigma$ - określa relację między natężeniem pola elektrycznego a gęstością prądu przewodzenia ( zal 2-11).
• Rodzaje ośrodków pod katem właściwości dla pola elektromagnetycznego:
  • Ośrodki liniowe i nieliniowe.
  • Ośrodki jednorodne i niejednorodne.
  • Ośrodki dyspersyjne i niedyspersyjne. Parametry materiałowe ośrodka dyspersyjnego zależą a ośrodka niedyspersyjnego nie zależą od częstotliwości.
  • Ośrodki izotropowe i anizotropowe. Parametry materiałowe ośrodka izotropowego nie zależą zaś ośrodka anizotropowego zależą od kierunku pola
• Warunki brzegowe na granicy dwóch dielektryków:
  • Nie ma prądów i ładunków powierzchniowych.
  • Składowe normalne wektorów indukcji $D$ i $B$ oraz składowe styczne wektorów natężenia pól $E$ i $H$ są ciągłe.
• Warunki brzegowe na granicy dielektryk idealny przewodnik: W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości:
  • Pole elektryczne musi być prostopadłe do przewodnika.
  • Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho\,\} równej indukcji elektrycznej $D$.
  • Pole magnetyczne musi być styczne do przewodnika.
  • Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej $j$ równej $H$.
• Równania Helmholtza - równania falowe dla pól harmonicznych w zapisie zespolonym.
• Stała propagacji – funkcja parametrów materiałowych ośrodka (zal 2-38). Wartość decyduje o szybkości zmian parametrów fali wzdłuż kierunku propagacji.
• Stała tłumienia część rzeczywista stałej propagacji, decyduje o szybkości strat mocy fali wzdłuż kierunku jej propagacji (zal. 2-51a)
• Stała fazowa część urojona stałej propagacji, decyduje o szybkości zmian fazy fali ( zal. 2-51b, 2-52b).
• Prędkość fazowa fali - prędkość z jaką przesuwa się płaszczyzna stałej fazy fali.
• Prędkość grupowa fali - jest prędkością przepływu energii.
• Fala płaska - Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Powierzchnia ekwifazowa fali płaskiej jest płaszczyzna prostopadłą do kierunku propagacji.
• Właściwości fali płaskiej - fala płaska jest falą typu TEM (Transverse Electro-Magnetic)
  • Wektory $E$ i $H$ fali TEM leżą w płaszczyźnie prostopadłej do kierunku propagacji i są prostopadłe względem siebie.
  • Zwrot iloczynu wektorowego pola $E$ razy pole $H$ wyznacza kierunek propagacji a jego moduł gęstość mocy fali.
  • Impedancja falowa (stosunek wartości wzajemnie prostopadłych składowych pola $E$ i $H$) fali płaskiej jest równy impedancji właściwej ośrodka.

---

Bibliografia

1. Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
2. Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
3. Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
4. Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.

---