PEE Moduł 11: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 344: | Linia 344: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd28.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd28.png|thumb|500px]] | ||
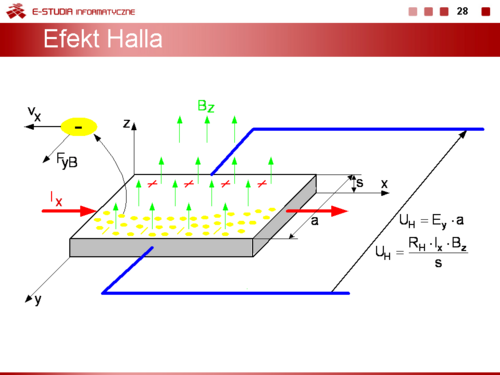
|valign="top"| | |valign="top"|'''Oddziaływanie pola magnetycznego na nośniki ładunku w półprzewodniku. Efekt Halla.''' | ||
Weźmy pod uwagę płytkę prostopadłościenną wykonaną z półprzewodnika typu n. | |||
W kierunku osi x poruszają się z prędkością <math>v_x</math> ładunki swobodne tworząc prąd <math>I_x</math> W kierunku prostopadłym do osi x, wzdłuż osi z, wytworzone zostało stałe pole magnetyczne | |||
o indukcji Bz. Pod wpływem tego pola tor ruchu poruszających się elektronów zostaje zakrzywiony w kierunku osi y. Żeby zrównoważyć siłę <math>F_y_B = - v_x•B_z</math> powodującą dryfowanie elektronów w kierunku tej siły, wewnątrz płytki półprzewodnikowej powstaje pole elektryczne <math>E_y</math> o zwrocie zgodnym z kierunkiem osi y. Kiedy siła <math>F_y_E = e•E_y</math> jest równa co do wartości sile F_y_B ustala się stan równowagi i elektrony mogą nadal przemieszczać się | |||
w płytce wzdłuż osi x. Powstawanie pola elektrycznego Ey nosi nazwę efektu Halla, a napięcie <math>U_H = E_y</math> a - napięciem Halla. Jeżeli płytka półprzewodnikowa będzie typu p zmienią się zwroty sił <math>F_y_B, F_y_E</math> oraz natężenia pola elektrycznego <math>E_y</math> i napięcia Halla <math>U_H</math>. Zjawisko Halla praktycznie zastosowano do badania przewodnictwa materiałów (w tym również metali) oraz do konstrukcji półprzewodnikowych czujników pola magnetycznego. | |||
|} | |} | ||
| Linia 351: | Linia 357: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd29.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd29.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Transport nośników nadmiarowych w półprzewodniku niesamoistnym. Dyfuzja.''' | ||
W półprzewodniku typu n nośnikami nadmiarowymi są elektrony, a w półprzewodniku typu p dziury. Jeżeli w pewnej objętości półprzewodnika znajdzie się więcej nośników nadmiarowych niż w innym oznacza to, że ich koncentracje w różnych obszarach materiału są różne. W tym wypadku nośniki z obszaru o większej koncentracji będą się przesuwały do obszaru o koncentracji mniejszej. Ten proces nazywamy dyfuzją. Dyfuzja jest naturalnym efektem przypadkowych ruchów poszczególnych nośników i występuje bez działania żadnej konwencjonalnej siły. Dyfuzja i unoszenie w polu elektrycznym to dwa podstawowe procesy transportu nośników w półprzewodnikach. W wyniku nierównomiernego rozkładu nośników w materiale półprzewodnika płynie prąd, który składa się z dwóch składników: prądu unoszenia pochodzącego od pola elektrycznego powstającego w wyniku rozsunięcia się ładunków w przestrzeni oraz prądu dyfuzji. | |||
|} | |} | ||
| Linia 358: | Linia 367: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd30.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd30.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W stanie równowagi termicznej suma prądu unoszenia i dyfuzji jest równa zeru. Dokładniejsze badanie warunków równowagi pozwala wyznaczyć tzw. zależność Einsteina wiążącą ruchliwość ładunku ze współczynnikiem dyfuzji: | ||
<math>\frac{D_n}{\mu_n}=\frac{D_p}{\mu_p}=\frac{kT}{e}=U_T</math> | |||
gdzie UT potencjał elektrokinetyczny. | |||
W temperaturze pokojowej <math>U_T</math> jest równe około 25 mV | |||
|} | |} | ||
| Linia 365: | Linia 380: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd31.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd31.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Przy niewielkich odchyleniach koncentracji nośników od stanu równowagi wypadkowa gęstość prądu elektronów i dziur jest równa: | ||
<math>J_n(X)=J_u_n+J_d_n=e\mu_n n(X)E_x+eD_n\frac{dn(X)}{dx}</math> | |||
<math>J_p(X)=J_u_p+J_d_p=e\mu_p p(X)E_x+eD_n\frac{dp(X)}{dx}</math> | |||
|} | |} | ||
| Linia 372: | Linia 394: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd32.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd32.png|thumb|500px]] | ||
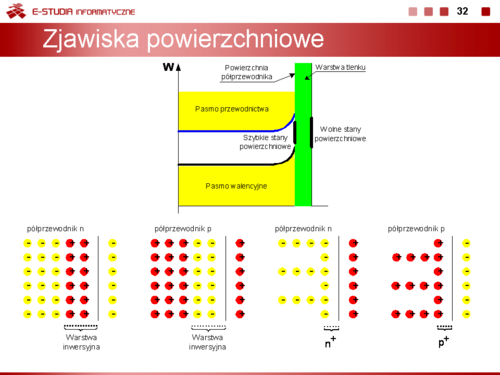
|valign="top"| | |valign="top"|'''Zjawiska powierzchniowe''' | ||
Na powierzchni półprzewodnika występuje w sposób naturalny nieciągłość sieci krystalicznej. W modelu pasmowym oznacza to, że pojawiają się na granicy materiału tzw. energetyczne stany powierzchniowe, które mogą być obsadzone przez elektrony. Stany te są one usytuowane w pobliżu środka pasma zabronionego. Wyróżnia się tzw. stany szybkie, powstające na powierzchni czystego półprzewodnika i stany wolne, w przypadku, gdy powierzchnia półprzewodnika pokryta jest warstwą tlenku. Stany powierzchniowe mogą być donorowe lub akceptorowe. Powodują one, że na powierzchni półprzewodnika w cienkiej warstwie o grubości od kilku do kilkudziesięciu angstremów <math>(1 Ǻ = 10^-^9 m)</math> gromadzi się ładunek ujemny (elektrony) lub dodatni (dziury). W wyniku oddziaływania tej warstwy na ładunki znajdujące się wewnątrz półprzewodnika w pobliżu jego powierzchni powstaje tzw. warstwa inwersyjna ładunku przeciwnego znaku | |||
|} | |} | ||
| Linia 379: | Linia 404: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd33.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd33.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Grubość warstwy inwersyjnej jest funkcją wnikania pola elektrycznego w półprzewodnik, a ta jest określona wzorem Debeya | ||
<math>L_D\sqrt \frac{2\epsilon \cdot \epsilon_0 \cdot k\cdot T}{n\cdot e^2}</math> | |||
gdzie | |||
<math>\epsilon</math> – względna przenikalność elektryczna krzemu | |||
<math>\epsilon_0</math> – przenikalność elektryczna próżni | |||
<math>N</math> – koncentracja domieszki: donorowej Nd lub akceptorowe Np. | |||
Wartość LD zawiera się w przedziale wartości <math>10^{-10}-10^{-8} m</math>. | |||
|} | |} | ||
| Linia 386: | Linia 421: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd34.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd34.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Szumy w półprzewodnikach''' | ||
Trzy zjawiska fizyczne są źródłem niezdeterminowanych, chaotycznych i niepożądanych sygnały występujących w materiałach, a w szczególności w półprzewodnikach stosowanych w elektronice, do budowy elementów elektronicznych: | |||
#Szumy cieplne. | |||
#Szumy śrutowe. | |||
#Szumy strukturalne. | |||
|} | |} | ||
| Linia 393: | Linia 435: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd35.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd35.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Szumy cieplne są spowodowane ciągłym, bezładnym ruchem swobodnych elektronów i dziur w materiale półprzewodnikowym. Wartość skuteczna napięcia, jakie w związku z tym ruchem powstaje, w zakresie częstotliwości <math>Δf</math> jest równa: | ||
<math>U_s_z=\sqrt kTRΔf</math> | |||
gdzie R – rezystancja próbki materiału | |||
|} | |} | ||
| Linia 400: | Linia 448: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd36.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd36.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Szumy śrutowe spowodowane są występowaniem statystycznych fluktuacji procesów związanych z generacją, rekombinacją i dyfuzją nośników ładunków w półprzewodniku podczas przepływu prądu. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>Δf</math> jest równa: | ||
<math>I_s_z=\sqrt 2eΔfi_0</math> | |||
gdzie <math>I_0</math> – składowa stała przepływającego przez próbkę prądu. | |||
|} | |} | ||
| Linia 407: | Linia 460: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd37.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd37.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Szumy strukturalne, czasami nazywane modulacyjnymi, wywołane są zjawiskami powierzchniowymi. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>Δf</math> maleje ze wzrostem częstotliwości i jest równa: | ||
<math>I_s_z=\sqrtAI_0\frac{Δf}{f}</math> | |||
gdzie A – stała zależna od wymiarów i parametrów materiału półprzewodnikowego. | |||
|} | |} | ||
| Linia 414: | Linia 472: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd38.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd38.png|thumb|500px]] | ||
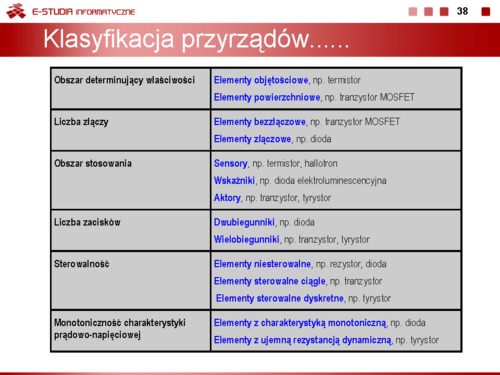
|valign="top"| | |valign="top"|'''Klasyfikacja przyrządów półprzewodnikowych''' | ||
Przyrządy półprzewodnikowe klasyfikujemy przyjmując różne kryteria podziału. Przyjmując jako kryterium liczbę złącz półprzewodnikowych dzielimy przyrządy półprzewodnikowe na bezzłączowe, jednozłączowe i wielozłączowe, a ze względu na liczbę wyprowadzeń na dwu-, trój- i wielozaciskowe. | |||
Ze względu na obszar, w którym zachodzą zjawiska fizyczne decydujące | |||
o właściwościach elektrycznych dzielimy przyrządy półprzewodnikowe na takie, w których występują efekty objętościowe (decydują zjawiska zachodzące w całej objętości materiału półprzewodnikowego) i takie, w których występują efekty powierzchniowe (decydują zjawiska zachodzące na powierzchni materiału półprzewodnikowego). | |||
Przyjmując jako kryterium możliwość wzmacniania sygnałów dzielimy przyrządy półprzewodnikowe na pasywne (tłumią sygnały) i aktywne (umożliwiają wzmacnianie sygnałów). | |||
Ze względu na możliwość zmiany stanu pracy elementu dzielimy przyrządy półprzewodnikowe na sterowalne i niesterowalne, a z punktu widzenia energetycznego na przyrządy małej mocy (sygnałowe) i przyrządy mocy (do pracy w układach energoelektronicznych). | |||
|} | |} | ||
---- | ---- | ||
{| | |||
|'''Literatura''' | |||
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, | |||
Oficyna Wydawnicza PW, Warszawa 2005 | |||
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, | |||
WNT, Warszawa 1981 | |||
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 | |||
|} | |||
Wersja z 13:28, 8 wrz 2006
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Tabela. Podstawowe materiały półprzewodnikowe |
 |
Przykłady defektów sieci krystalicznej |
 |
Obszar, w którym zachodzi bardzo silna (o kilka rzędów wielkości) zmiana koncentracji ładunku i typu przewodnictwa nazywa się złączem.
Szerokość złącza ma na ogół wymiar rzędu .
|
 |
Przy niewielkich odchyleniach koncentracji nośników od stanu równowagi wypadkowa gęstość prądu elektronów i dziur jest równa:
|
| Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005 J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981 P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 |