PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd1.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd1.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 90: | Linia 90: | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd5.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd5.png|500px]] | ||
|valign="top"|W przypadku obwodów liniowych funkcje <math>f_i(t)</math> występujące po prawej stronie wzoru są liniowymi funkcjami wymuszeń prądowych i napięciowych. Oznaczając wymuszenia prądowe bądź napięciowe w ogólności przez <math>u_i (i=1, 2,...,m)</math> można opis stanowy obwodu przedstawić w postaci | |valign="top"|W przypadku obwodów liniowych funkcje <math>f_i(t)</math> występujące po prawej stronie wzoru są liniowymi funkcjami wymuszeń prądowych i napięciowych. Oznaczając wymuszenia prądowe bądź napięciowe w ogólności przez <math>u_i (i=1, 2,...,m)</math> można opis stanowy obwodu przedstawić w postaci | ||
: <math>\frac{d\mathbf{x}(t)}{dt}=\mathbf{Ax}(t)+\mathbf{Bu}(t)</math> | : <math>\frac{d\mathbf{x}(t)}{dt}=\mathbf{Ax}(t)+\mathbf{Bu}(t)</math> | ||
gdzie <math>\mathbf{A}\,</math> jest macierzą stanu o wymiarach <math>n×n\,</math> zawierającą elementy <math>a_i_j\,</math>, a macierz <math>\mathbf{B}\,</math> o wymiarach <math>n×m\,</math> składa się ze współczynników uzależniających pochodną zmiennych stanu od wektora wymuszeń <math>\mathbf{u}\,</math>. | gdzie <math>\mathbf{A}\,</math> jest macierzą stanu o wymiarach <math>n×n\,</math> zawierającą elementy <math>a_i_j\,</math>, a macierz <math>\mathbf{B}\,</math> o wymiarach <math>n×m\,</math> składa się ze współczynników uzależniających pochodną zmiennych stanu od wektora wymuszeń <math>\mathbf{u}\,</math>. | ||
| Linia 100: | Linia 98: | ||
Równanie nazywane jest macierzowym równaniem stanu obwodu elektrycznego. Rozwiązanie tego równania pozwala wyznaczyć przebiegi czasowe zmiennych stanu tworzących wektor <math>\mathbf{x}(t)\,</math>. Jeśli dodatkowo interesują nas inne zmienne w obwodzie, na przykład prądy i napięcia rezystorów, prądy kondensatorów czy napięcia na cewkach to należy sformułować drugie równanie, tzw. równanie odpowiedzi <math>\mathbf{y}(t)\,</math>, które uzależnia poszukiwane wielkości od zmiennych stanu i wymuszeń. Równanie to zapiszemy w postaci | Równanie nazywane jest macierzowym równaniem stanu obwodu elektrycznego. Rozwiązanie tego równania pozwala wyznaczyć przebiegi czasowe zmiennych stanu tworzących wektor <math>\mathbf{x}(t)\,</math>. Jeśli dodatkowo interesują nas inne zmienne w obwodzie, na przykład prądy i napięcia rezystorów, prądy kondensatorów czy napięcia na cewkach to należy sformułować drugie równanie, tzw. równanie odpowiedzi <math>\mathbf{y}(t)\,</math>, które uzależnia poszukiwane wielkości od zmiennych stanu i wymuszeń. Równanie to zapiszemy w postaci | ||
: <math>\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{Du}(t)</math> | : <math>\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{Du}(t)</math> | ||
Równania tworzą parę równań stanu | Równania tworzą parę równań stanu | ||
| Linia 114: | Linia 110: | ||
która w pełni opisuje stan obwodu przy założeniu, że znane są warunki początkowe <math>\mathbf{x}_0=\mathbf{x}(t0)</math>, gdzie <math>t_0\,</math> oznacza chwilę przełączenia. W przypadku ogólnym rozwiązanie równania stanu przyjmuje postać | która w pełni opisuje stan obwodu przy założeniu, że znane są warunki początkowe <math>\mathbf{x}_0=\mathbf{x}(t0)</math>, gdzie <math>t_0\,</math> oznacza chwilę przełączenia. W przypadku ogólnym rozwiązanie równania stanu przyjmuje postać | ||
: <math>\mathbf{x}(t)=e^{\mathbf{A}(t-t_0)}\mathbf{x}(t_0)+\int_{t_0}^t e^{\mathbf{A}(t-\tau)}\mathbf{Bu}(\tau)d\tau</math> | : <math>\mathbf{x}(t)=e^{\mathbf{A}(t-t_0)}\mathbf{x}(t_0)+\int_{t_0}^t e^{\mathbf{A}(t-\tau)}\mathbf{Bu}(\tau)d\tau</math> | ||
Zależność powyższa stanowi rozwiązanie ogólne, które dla konkretnych wartości funkcji wymuszających zadanych wektorem u wyznacza rozwiązanie czasowe dla zmiennych stanu. We współczesnych metodach numerycznych równania stanu stanowią punkt wyjścia w określaniu dokładnego rozwiązania równań liniowych lub przybliżonego dla zlinearyzowanych równań stanu. | Zależność powyższa stanowi rozwiązanie ogólne, które dla konkretnych wartości funkcji wymuszających zadanych wektorem u wyznacza rozwiązanie czasowe dla zmiennych stanu. We współczesnych metodach numerycznych równania stanu stanowią punkt wyjścia w określaniu dokładnego rozwiązania równań liniowych lub przybliżonego dla zlinearyzowanych równań stanu. | ||
Wersja z 09:25, 8 wrz 2006

|

|
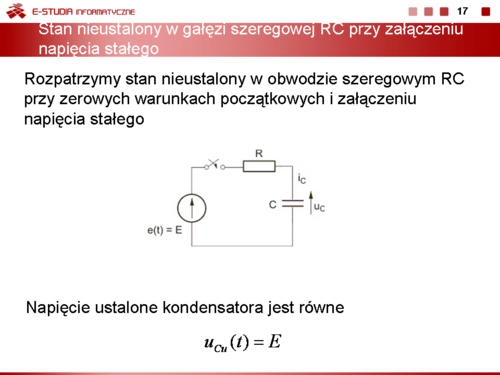
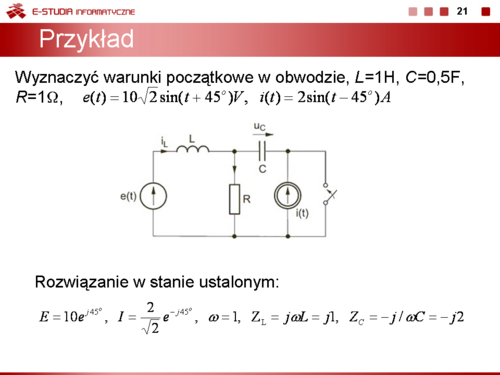
Równania obwodu w stanie ustalonym
|
| Zadania sprawdzające
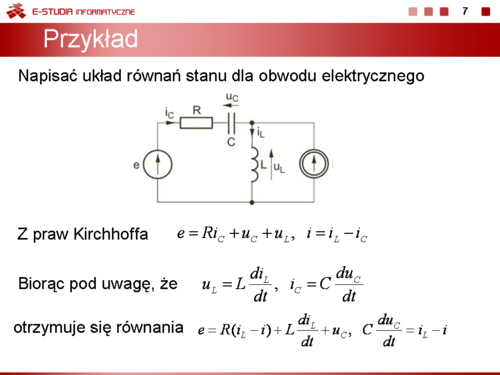
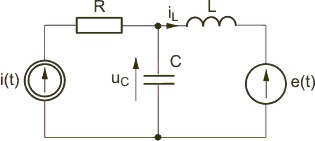
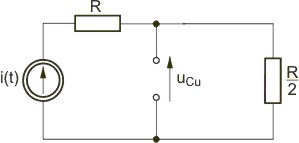
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku
Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
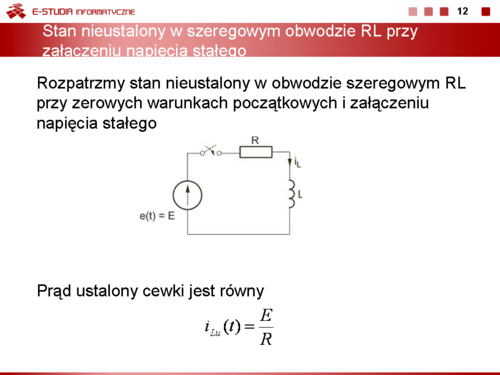
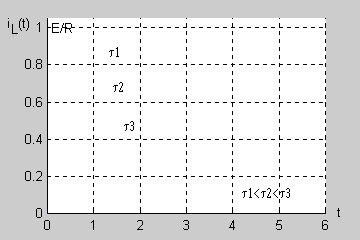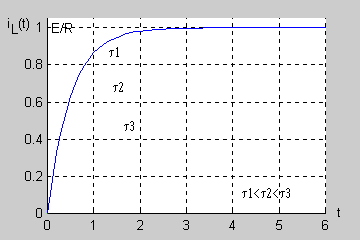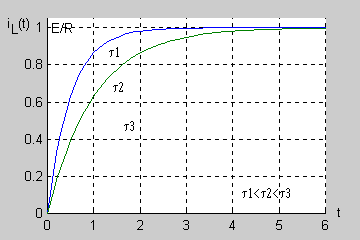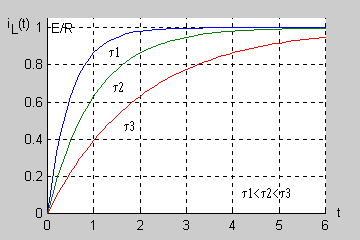
Zadanie 7.2 Określić przebieg czasowy napięcia na kondensatorze w stanie nieustalonym w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów: .
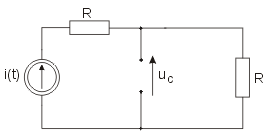
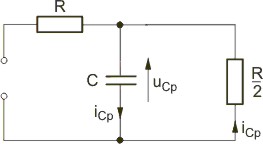
Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
Schemat obwodu w stanie ustalonym po przełączeniu
Schemat obwodu w stanie przejściowym po przełączeniu
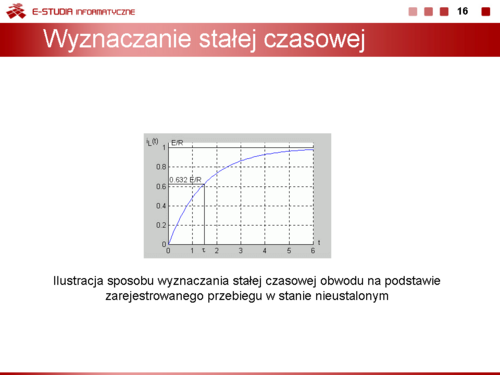
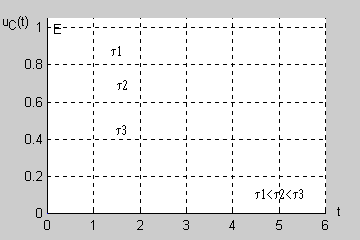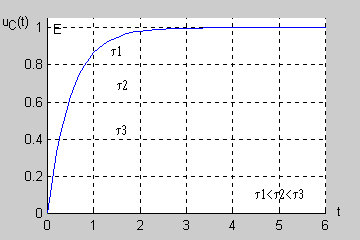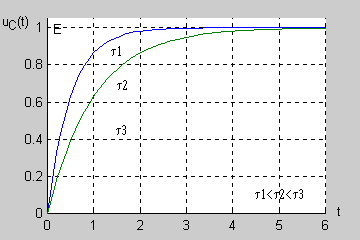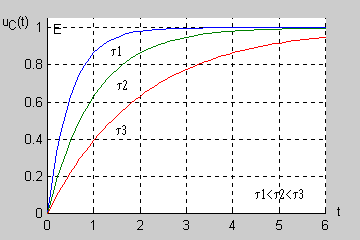
Stała czasowa obwodu jest więc równa . |