PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd1.png|500px]] | ||
|valign="top"|'''Wykład 5. Obwody ze sprzężeniami magnetycznymi''' | |valign="top"|'''Wykład 5. Obwody ze sprzężeniami magnetycznymi''' | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd2.png|500px]] | ||
|valign="top"|'''Zjawiska fizyczne przy sprzężeniu magnetycznym cewek''' | |valign="top"|'''Zjawiska fizyczne przy sprzężeniu magnetycznym cewek''' | ||
| Linia 19: | Linia 19: | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd3.png|500px]] | ||
|valign="top"|Strumień <math>\psi_1_1</math> występujący w cewce pierwszej pochodzi od prądu tej cewki a strumień <math>\psi_2_1</math> jest wytworzony przez cewkę drugą i przenika przez cewkę pierwszą. Podobnie strumień <math>\psi_2_2</math> pojawiający się w cewce drugiej pochodzi od prądu tej cewki a strumień <math>\psi_1_2</math> pochodzący od prądu cewki pierwszej przenika przez cewkę drugą. Uwzględniając pojęcie indukcyjności własnej i wzajemnej wprowadzone w rozdziale pierwszym dla cewek liniowych sprzężonych magnetycznie obowiązują następujące relacje: | |valign="top"|Strumień <math>\psi_1_1</math> występujący w cewce pierwszej pochodzi od prądu tej cewki a strumień <math>\psi_2_1</math> jest wytworzony przez cewkę drugą i przenika przez cewkę pierwszą. Podobnie strumień <math>\psi_2_2</math> pojawiający się w cewce drugiej pochodzi od prądu tej cewki a strumień <math>\psi_1_2</math> pochodzący od prądu cewki pierwszej przenika przez cewkę drugą. Uwzględniając pojęcie indukcyjności własnej i wzajemnej wprowadzone w rozdziale pierwszym dla cewek liniowych sprzężonych magnetycznie obowiązują następujące relacje: | ||
| Linia 43: | Linia 43: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd4.png|500px]] | ||
|valign="top"|Sprzężenie magnetyczne powoduje indukowanie się napięcia w cewce od zmian prądu własnego cewki i od zmian prądu cewki z nią sprzężonej. Wzory określające odpowiednie napięcia na cewkach sprzężonych magnetycznie dane są wówczas w postaci | |valign="top"|Sprzężenie magnetyczne powoduje indukowanie się napięcia w cewce od zmian prądu własnego cewki i od zmian prądu cewki z nią sprzężonej. Wzory określające odpowiednie napięcia na cewkach sprzężonych magnetycznie dane są wówczas w postaci | ||
| Linia 61: | Linia 61: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd5.png|500px]] | ||
|valign="top"|Rysunek obok ilustruje schematyczne oznaczenia sprzężenia dodatniego i ujemnego dwóch cewek. | |valign="top"|Rysunek obok ilustruje schematyczne oznaczenia sprzężenia dodatniego i ujemnego dwóch cewek. | ||
| Linia 72: | Linia 72: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd6.png|500px]] | ||
|valign="top"|'''Równania symboliczne elementów sprzężonych magnetycznie''' | |valign="top"|'''Równania symboliczne elementów sprzężonych magnetycznie''' | ||
| Linia 91: | Linia 91: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd7.png|500px]] | ||
|valign="top"|Napięcie skuteczne zespolone na cewkach sprzężonych można wówczas opisać następującymi wzorami | |valign="top"|Napięcie skuteczne zespolone na cewkach sprzężonych można wówczas opisać następującymi wzorami | ||
| Linia 106: | Linia 106: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd8.png|500px]] | ||
|valign="top"|Najważniejszym elementem analizy obwodów ze sprzężeniami magnetycznymi jest wyznaczenie prądów poszczególnych gałęzi w obwodzie. Bezpośrednie zastosowanie poznanych dotąd metod analizy obwodów (metoda węzłowa, oczkowa, Thevenina czy Nortona) wymaga w pierwszej kolejności wyeliminowania sprzężenia magnetycznego cewek, a więc pozbycia się wpływu prądu jednej cewki na napięcie cewki drugiej | |valign="top"|Najważniejszym elementem analizy obwodów ze sprzężeniami magnetycznymi jest wyznaczenie prądów poszczególnych gałęzi w obwodzie. Bezpośrednie zastosowanie poznanych dotąd metod analizy obwodów (metoda węzłowa, oczkowa, Thevenina czy Nortona) wymaga w pierwszej kolejności wyeliminowania sprzężenia magnetycznego cewek, a więc pozbycia się wpływu prądu jednej cewki na napięcie cewki drugiej | ||
| Linia 120: | Linia 120: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd9.png|500px]] | ||
|valign="top"|Rysunek na slajdzie obok pokazuje oznaczenie cewek jednoimiennych i różnoimiennych spełniających warunki podane na poprzednim slajdzie. | |valign="top"|Rysunek na slajdzie obok pokazuje oznaczenie cewek jednoimiennych i różnoimiennych spełniających warunki podane na poprzednim slajdzie. | ||
| Linia 129: | Linia 129: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd10.png|500px]] | ||
|valign="top"|W przypadku cewek jednoimiennych eliminacja sprzężenia magnetycznego prowadzi do obwodu zastępczego przedstawionego na slajdzie obok. W gałęziach zawierających cewki pojawiła się impedancja wzajemna ze znakiem plus a w gałęzi wspólnej impedancja wzajemna ze znakiem minus. | |valign="top"|W przypadku cewek jednoimiennych eliminacja sprzężenia magnetycznego prowadzi do obwodu zastępczego przedstawionego na slajdzie obok. W gałęziach zawierających cewki pojawiła się impedancja wzajemna ze znakiem plus a w gałęzi wspólnej impedancja wzajemna ze znakiem minus. | ||
| Linia 147: | Linia 147: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd11.png|500px]] | ||
|valign="top"|Jako przykład rozpatrzymy eliminację sprzężeń 3 cewek sprzężonych magnetycznie ze sobą. | |valign="top"|Jako przykład rozpatrzymy eliminację sprzężeń 3 cewek sprzężonych magnetycznie ze sobą. | ||
| Linia 160: | Linia 160: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd12.png|500px]] | ||
|valign="top"|Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym. | |valign="top"|Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym. | ||
| Linia 169: | Linia 169: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd13.png|500px]] | ||
|valign="top"|Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. | |valign="top"|Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. | ||
|} | |} | ||
| Linia 176: | Linia 176: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd14.png|500px]] | ||
|valign="top"|Rozwiązanie obwodu przebiega w następującej kolejności. | |valign="top"|Rozwiązanie obwodu przebiega w następującej kolejności. | ||
| Linia 198: | Linia 198: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd15.png|500px]] | ||
|valign="top"|Napięcie <math>U_{AB}\,</math> | |valign="top"|Napięcie <math>U_{AB}\,</math> | ||
| Linia 223: | Linia 223: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd16.png|500px]] | ||
|valign="top"|'''Podstawy fizyczne działania transformatora''' | |valign="top"|'''Podstawy fizyczne działania transformatora''' | ||
| Linia 234: | Linia 234: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd17.png|500px]] | ||
|valign="top"|Przekazywanie energii elektrycznej z jednego obwodu do drugiego następuje za pośrednictwem pola elektromagnetycznego (strumienia magnetycznego). Na rysunku przedstawiono poglądowy schemat transformatora zasilanego napięciem <math>U_1\,</math> i obciążonego po stronie wtórnej impedancją <math>Z_o\,</math>. Uzwojenie, do którego jest zazwyczaj doprowadzone źródło energii elektrycznej, nazywamy uzwojeniem pierwotnym, natomiast uzwojenie, do którego jest dołączony odbiornik, nazywamy uzwojeniem wtórnym. Zaciski uzwojenia pierwotnego stanowią wejście układu, a zaciski uzwojenia wtórnego - wyjście. Odpowiednie napięcia i prądy w transformatorze nazywamy pierwotnymi lub wtórnymi. Wszystkie wielkości i parametry związane z uzwojeniem pierwotnym opatrzymy wskaźnikiem 1, a wielkości i parametry związane z uzwojeniem wtórnym – wskaźnikiem 2. | |valign="top"|Przekazywanie energii elektrycznej z jednego obwodu do drugiego następuje za pośrednictwem pola elektromagnetycznego (strumienia magnetycznego). Na rysunku przedstawiono poglądowy schemat transformatora zasilanego napięciem <math>U_1\,</math> i obciążonego po stronie wtórnej impedancją <math>Z_o\,</math>. Uzwojenie, do którego jest zazwyczaj doprowadzone źródło energii elektrycznej, nazywamy uzwojeniem pierwotnym, natomiast uzwojenie, do którego jest dołączony odbiornik, nazywamy uzwojeniem wtórnym. Zaciski uzwojenia pierwotnego stanowią wejście układu, a zaciski uzwojenia wtórnego - wyjście. Odpowiednie napięcia i prądy w transformatorze nazywamy pierwotnymi lub wtórnymi. Wszystkie wielkości i parametry związane z uzwojeniem pierwotnym opatrzymy wskaźnikiem 1, a wielkości i parametry związane z uzwojeniem wtórnym – wskaźnikiem 2. | ||
| Linia 247: | Linia 247: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd18.png|500px]] | ||
|valign="top"|'''Transformator idealny''' | |valign="top"|'''Transformator idealny''' | ||
| Linia 258: | Linia 258: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd19.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd19.png|500px]] | ||
|valign="top"|Transformator idealny jest w pełni opisany poprzez tak zwaną '''przekładnię zwojową''', określającą stosunek napięcia pierwotnego do wtórnego ('''przekładnię napięciową''') na podstawie liczby zwojów pierwotnych i wtórnych. Przekładnia napięciowa transformatora idealnego niezależnie od sposobu wykonania i od obciążenia, powinna być równa przekładni zwojowej określonej wzorem | |valign="top"|Transformator idealny jest w pełni opisany poprzez tak zwaną '''przekładnię zwojową''', określającą stosunek napięcia pierwotnego do wtórnego ('''przekładnię napięciową''') na podstawie liczby zwojów pierwotnych i wtórnych. Przekładnia napięciowa transformatora idealnego niezależnie od sposobu wykonania i od obciążenia, powinna być równa przekładni zwojowej określonej wzorem | ||
| Linia 281: | Linia 281: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd20.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd20.png|500px]] | ||
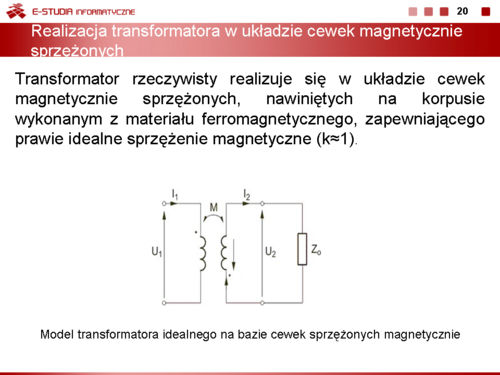
|valign="top"|'''Realizacja transformatora w układzie cewek magnetycznie sprzężonych''' | |valign="top"|'''Realizacja transformatora w układzie cewek magnetycznie sprzężonych''' | ||
| Linia 292: | Linia 292: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd21.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd21.png|500px]] | ||
|valign="top"|Analizując transformator w stanie ustalonym przy wymuszeniu sinusoidalnym zastosujemy metodę symboliczną. Z definicji sprzężenia magnetycznego obu cewek przy założonym zwrocie prądów i przyjęciu początków uzwojeń jak na rysunku wynikają następujące równania opisujące obwód | |valign="top"|Analizując transformator w stanie ustalonym przy wymuszeniu sinusoidalnym zastosujemy metodę symboliczną. Z definicji sprzężenia magnetycznego obu cewek przy założonym zwrocie prądów i przyjęciu początków uzwojeń jak na rysunku wynikają następujące równania opisujące obwód | ||
| Linia 311: | Linia 311: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd22.png|500px]] | ||
|valign="top"|Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji <math>X_{L1}=Kz_1^2, X_{L2}=Kz_2^2, X_M=Kz_1z_2</math> gdzie <math>K</math> oznacza pewną stałą konstrukcyjną, to z zależności wynika | |valign="top"|Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji <math>X_{L1}=Kz_1^2, X_{L2}=Kz_2^2, X_M=Kz_1z_2</math> gdzie <math>K</math> oznacza pewną stałą konstrukcyjną, to z zależności wynika | ||
| Linia 322: | Linia 322: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd23.png|500px]] | ||
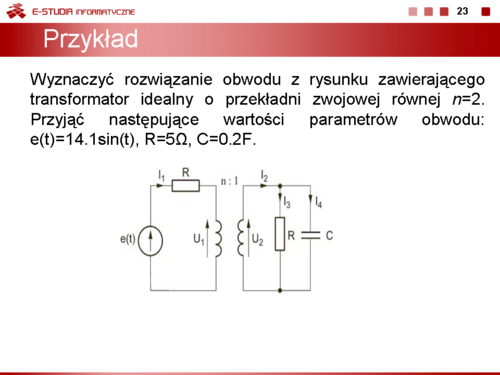
|valign="top"|Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej <math>n=2\,</math>. Przyjmiemy następujące wartości parametrów obwodu: <math>e(t)=10\sqrt2sin(\omega t)V</math>, <math>\omega=1rad/s</math>, <math>R=5\Omega</math>, <math>C=0,2F</math>. | |valign="top"|Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej <math>n=2\,</math>. Przyjmiemy następujące wartości parametrów obwodu: <math>e(t)=10\sqrt2sin(\omega t)V</math>, <math>\omega=1rad/s</math>, <math>R=5\Omega</math>, <math>C=0,2F</math>. | ||
|} | |} | ||
| Linia 329: | Linia 329: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd24.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd24.png|500px]] | ||
|valign="top"|Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami | |valign="top"|Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami | ||
| Linia 353: | Linia 353: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd25.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd25.png|500px]] | ||
|valign="top"|Po wstawieniu wartości liczbowych otrzymuje się | |valign="top"|Po wstawieniu wartości liczbowych otrzymuje się | ||
Wersja z 12:19, 6 wrz 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |

|
Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym.
Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. |

|
Rozwiązanie obwodu przebiega w następującej kolejności.
Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu:
|
|
Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej . Przyjmiemy następujące wartości parametrów obwodu: , , , . |

|
Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami
|

|
Po wstawieniu wartości liczbowych otrzymuje się
|