PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd1.png|500px]] | ||
|valign="top"|'''Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym''' | |valign="top"|'''Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym''' | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd2.png|500px]] | ||
|valign="top"|'''Metoda równań Kirchhoffa''' | |valign="top"|'''Metoda równań Kirchhoffa''' | ||
| Linia 19: | Linia 19: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd3.png|500px]] | ||
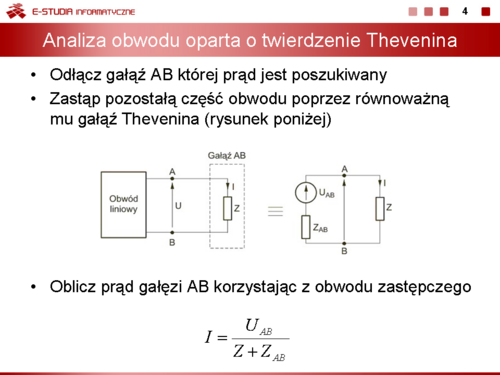
|valign="top"|'''Metoda oparta na twierdzeniu Thevenina''' | |valign="top"|'''Metoda oparta na twierdzeniu Thevenina''' | ||
| Linia 32: | Linia 32: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd4.png|500px]] | ||
|valign="top"|Na rysunku obok (slajd 4) przedstawiono sposób transformacji obwodu zgodnie z twierdzeniem Thevenina ułatwiający obliczenie prądu w wybranej gałęzi AB obwodu. | |valign="top"|Na rysunku obok (slajd 4) przedstawiono sposób transformacji obwodu zgodnie z twierdzeniem Thevenina ułatwiający obliczenie prądu w wybranej gałęzi AB obwodu. | ||
| Linia 45: | Linia 45: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd5.png|500px]] | ||
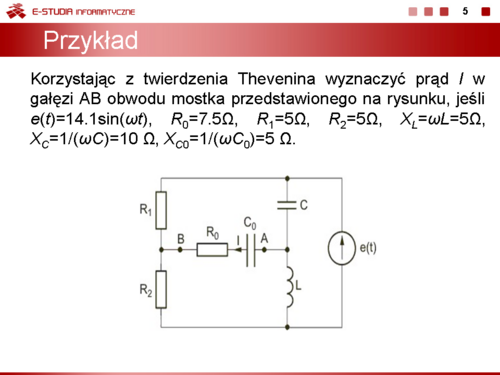
|valign="top"|Jako przykład rozpatrzymy obliczenie prądu w gałęzi AB obwodu przedstawionego na slajdzie. | |valign="top"|Jako przykład rozpatrzymy obliczenie prądu w gałęzi AB obwodu przedstawionego na slajdzie. | ||
| Linia 54: | Linia 54: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png|500px]] | ||
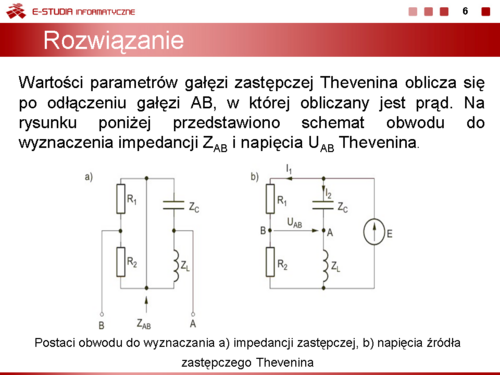
|valign="top"|W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: <math>Z_{AB}</math> i <math>U_{AB}</math>. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. | |valign="top"|W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: <math>Z_{AB}</math> i <math>U_{AB}</math>. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. | ||
| Linia 65: | Linia 65: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png|500px]] | ||
|valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | |valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | ||
| Linia 84: | Linia 84: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png|500px]] | ||
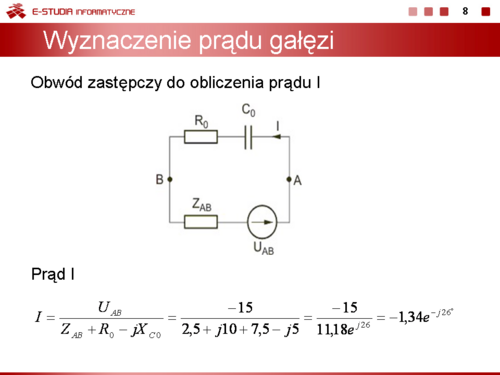
|valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\,</math> określa się ze wzoru | |valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\,</math> określa się ze wzoru | ||
| Linia 99: | Linia 99: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd9.png|500px]] | ||
|valign="top"|'''Metoda oparta na twierdzeniu Nortona''' | |valign="top"|'''Metoda oparta na twierdzeniu Nortona''' | ||
| Linia 113: | Linia 113: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd10.png|500px]] | ||
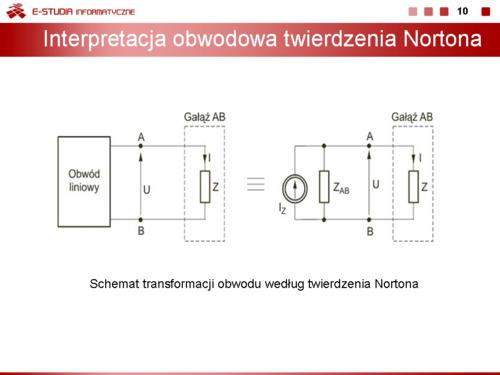
|valign="top"|Rysunek na slajdzie 10 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona. | |valign="top"|Rysunek na slajdzie 10 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona. | ||
| Linia 126: | Linia 126: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd11.png|500px]] | ||
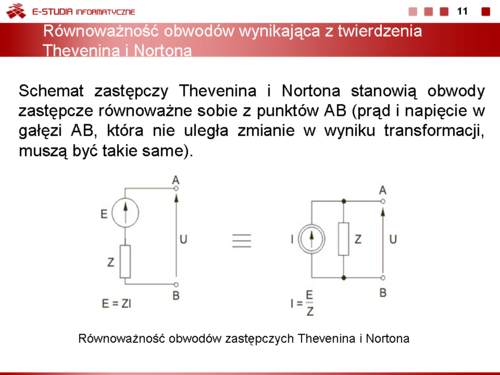
|valign="top"|'''Równoważność twierdzenia Thevenina i Nortona''' | |valign="top"|'''Równoważność twierdzenia Thevenina i Nortona''' | ||
| Linia 145: | Linia 145: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd12.png|500px]] | ||
|valign="top"|'''Metoda potencjałów węzłowych''' | |valign="top"|'''Metoda potencjałów węzłowych''' | ||
| Linia 156: | Linia 156: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd13.png|500px]] | ||
|valign="top"|Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci | |valign="top"|Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci | ||
| Linia 193: | Linia 193: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd14.png|500px]] | ||
|valign="top"|Elementy <math>Y_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Y}\,</math> nazywane są '''admitancjami własnymi''' węzła <math>i\,</math>-tego. W przypadku obwodów RLC bez źródeł sterowanych admitancja własna węzła <math>i\,</math>-tego jest równa sumie admitancji wszystkich gałęzi włączonych w <math>i\,</math>-tym węźle. Elementy <math>Y_{ij}</math> położone poza główną diagonalną są '''admitancjami wzajemnymi''' między węzłem <math>i\,</math>-tym oraz <math>j\,</math>-tym. Admitancja wzajemna dwu węzłów jest równa admitancji łączącej te węzły wziętej ze znakiem minus. Admitancja wzajemna węzła <math>i\,</math>-tego oraz <math>j\,</math>-tego jest taka sama jak węzła <math>j\,</math>-tego oraz <math>i\,</math>-tego, tzn. <math>Y_{ij}=Y_{ji}</math>. Macierz admitancyjna <math>\mathbf{Y}\,</math> dla obwodów RLC bez źródeł sterowanych jest więc macierzą symetryczną. | |valign="top"|Elementy <math>Y_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Y}\,</math> nazywane są '''admitancjami własnymi''' węzła <math>i\,</math>-tego. W przypadku obwodów RLC bez źródeł sterowanych admitancja własna węzła <math>i\,</math>-tego jest równa sumie admitancji wszystkich gałęzi włączonych w <math>i\,</math>-tym węźle. Elementy <math>Y_{ij}</math> położone poza główną diagonalną są '''admitancjami wzajemnymi''' między węzłem <math>i\,</math>-tym oraz <math>j\,</math>-tym. Admitancja wzajemna dwu węzłów jest równa admitancji łączącej te węzły wziętej ze znakiem minus. Admitancja wzajemna węzła <math>i\,</math>-tego oraz <math>j\,</math>-tego jest taka sama jak węzła <math>j\,</math>-tego oraz <math>i\,</math>-tego, tzn. <math>Y_{ij}=Y_{ji}</math>. Macierz admitancyjna <math>\mathbf{Y}\,</math> dla obwodów RLC bez źródeł sterowanych jest więc macierzą symetryczną. | ||
| Linia 202: | Linia 202: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd15.png|500px]] | ||
|valign="top"|Podsumowując, analiza obwodów w stanie ustalonym metoda węzłową wymaga wykonania następujących etapów: | |valign="top"|Podsumowując, analiza obwodów w stanie ustalonym metoda węzłową wymaga wykonania następujących etapów: | ||
*Opis obwodu równaniem macierzowym potencjałów węzłowych (zmienne poszukiwane: wektor potencjałów <math>\mathbf{V}\,</math>) | *Opis obwodu równaniem macierzowym potencjałów węzłowych (zmienne poszukiwane: wektor potencjałów <math>\mathbf{V}\,</math>) | ||
| Linia 214: | Linia 214: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd16.png|500px]] | ||
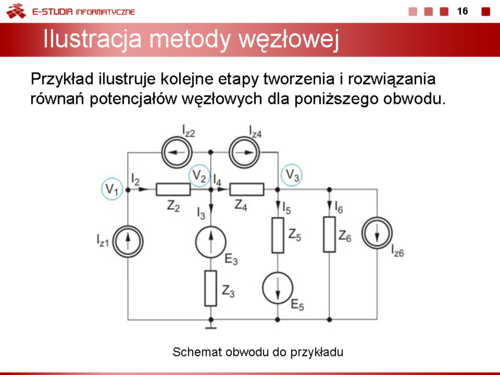
|valign="top"|Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rysunku obok. | |valign="top"|Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rysunku obok. | ||
| Linia 223: | Linia 223: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd17.png|500px]] | ||
|valign="top"|Obwód zawiera 3 węzły niezależne: <math>V_1</math>, <math>V_2</math> oraz <math>V_3</math> mierzone względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez <math>Y_i\,</math>, gdzie <math>Y_i=1/Z_i</math> otrzymuje się macierz potencjałów węzłowych <math>\mathbf{Y}\,</math> oraz wektor prądów wymuszających <math>\mathbf{I}_{zr}</math> w postaci | |valign="top"|Obwód zawiera 3 węzły niezależne: <math>V_1</math>, <math>V_2</math> oraz <math>V_3</math> mierzone względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez <math>Y_i\,</math>, gdzie <math>Y_i=1/Z_i</math> otrzymuje się macierz potencjałów węzłowych <math>\mathbf{Y}\,</math> oraz wektor prądów wymuszających <math>\mathbf{I}_{zr}</math> w postaci | ||
| Linia 267: | Linia 267: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd18.png|500px]] | ||
|valign="top"|Na podstawie obliczonych wartości napięć węzłowych obwodu można w prosty sposób korzystając z prawa napięciowego Kirchhoffa dla poszczególnych gałęzi obwodu wyznaczyć prądy gałęziowe. Wystarczy w tym celu zastosować bądź prawo Ohma (jeśli gałąź zawiera jedynie element pasywny) lub równanie napięciowe Kirchoffa dla gałęzi szeregowej zawierającej źródło napięcia i element pasywny. Przykładowo dla obwodu z rysunku na slajdzie 16 odpowiednie zależności przyjmują postać: | |valign="top"|Na podstawie obliczonych wartości napięć węzłowych obwodu można w prosty sposób korzystając z prawa napięciowego Kirchhoffa dla poszczególnych gałęzi obwodu wyznaczyć prądy gałęziowe. Wystarczy w tym celu zastosować bądź prawo Ohma (jeśli gałąź zawiera jedynie element pasywny) lub równanie napięciowe Kirchoffa dla gałęzi szeregowej zawierającej źródło napięcia i element pasywny. Przykładowo dla obwodu z rysunku na slajdzie 16 odpowiednie zależności przyjmują postać: | ||
| Linia 286: | Linia 286: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd19.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd19.png|500px]] | ||
|valign="top"|Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Dzięki takiemu założeniu są one bardzo proste i łatwe w stosowaniu. | |valign="top"|Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Dzięki takiemu założeniu są one bardzo proste i łatwe w stosowaniu. | ||
| Linia 295: | Linia 295: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd20.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd20.png|500px]] | ||
|valign="top"|'''Metoda prądów oczkowych (oczkowa)''' | |valign="top"|'''Metoda prądów oczkowych (oczkowa)''' | ||
| Linia 304: | Linia 304: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd21.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd21.png|500px]] | ||
|valign="top"|Oznaczmy w ogólności wektor prądów oczkowych w postaci | |valign="top"|Oznaczmy w ogólności wektor prądów oczkowych w postaci | ||
| Linia 345: | Linia 345: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd22.png|500px]] | ||
|valign="top"|Elementy <math>Z_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Z}\,</math> nazywamy '''impedancjami własnymi''' oczka <math>i\,</math>-tego. Elementy <math>Z_{ij}</math> położone poza główną diagonalną są '''impedancjami wzajemnymi''' między oczkiem <math>i\,</math>-tym oraz <math>j\,</math>-tym. Impedancja wzajemna dwu oczek przy identycznym zwrocie wszystkich prądów oczkowych jest równa impedancji wspólnej dla obu oczek wziętej ze znakiem minus. | |valign="top"|Elementy <math>Z_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Z}\,</math> nazywamy '''impedancjami własnymi''' oczka <math>i\,</math>-tego. Elementy <math>Z_{ij}</math> położone poza główną diagonalną są '''impedancjami wzajemnymi''' między oczkiem <math>i\,</math>-tym oraz <math>j\,</math>-tym. Impedancja wzajemna dwu oczek przy identycznym zwrocie wszystkich prądów oczkowych jest równa impedancji wspólnej dla obu oczek wziętej ze znakiem minus. | ||
|} | |} | ||
| Linia 352: | Linia 352: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd23.png|500px]] | ||
|valign="top"|Przy założeniu, że wszystkie prądy oczkowe mają identyczny zwrot, dla obwodów RLC bez źródeł sterowanych impedancja własna oczka <math>i\,</math>-tego jest równa sumie impedancji wszystkich gałęzi występujących w oczku. | |valign="top"|Przy założeniu, że wszystkie prądy oczkowe mają identyczny zwrot, dla obwodów RLC bez źródeł sterowanych impedancja własna oczka <math>i\,</math>-tego jest równa sumie impedancji wszystkich gałęzi występujących w oczku. | ||
| Linia 363: | Linia 363: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd24.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd24.png|500px]] | ||
|valign="top"|Sposób tworzenia opisu oczkowego zilustrujemy na przykładzie obwodu z rysunku na slajdzie. | |valign="top"|Sposób tworzenia opisu oczkowego zilustrujemy na przykładzie obwodu z rysunku na slajdzie. | ||
Dla podanego obwodu napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. Obwód zawiera 3 oczka niezależne, stąd wymiar macierzy oczkowej <math>\mathbf{Z}</math> jest równy 3, podobnie jak liczba nieznanych składników wektora prądów oczkowych oraz liczba znanych składników wektora napięć wymuszających. | Dla podanego obwodu napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. Obwód zawiera 3 oczka niezależne, stąd wymiar macierzy oczkowej <math>\mathbf{Z}</math> jest równy 3, podobnie jak liczba nieznanych składników wektora prądów oczkowych oraz liczba znanych składników wektora napięć wymuszających. | ||
| Linia 371: | Linia 371: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd25.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd25.png|500px]] | ||
|valign="top"|Korzystając z podanej wcześniej reguły tworzenia opisu oczkowego otrzymuje się | |valign="top"|Korzystając z podanej wcześniej reguły tworzenia opisu oczkowego otrzymuje się | ||
| Linia 397: | Linia 397: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd26.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd26.png|500px]] | ||
|valign="top"|Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie | |valign="top"|Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie | ||
| Linia 416: | Linia 416: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd27.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd27.png|500px]] | ||
|valign="top"|Metoda prądów oczkowych wymaga rozwiązania układu <math>N\,</math> równań, gdzie <math>N\,</math> oznacza liczbę oczek niezależnych. Podobnie jak w metodzie węzłowej liczba oczek jest zwykle dużo mniejsza niż liczba gałęzi obwodu, stąd metoda prądów oczkowych jest dużo bardziej efektywna niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa. | |valign="top"|Metoda prądów oczkowych wymaga rozwiązania układu <math>N\,</math> równań, gdzie <math>N\,</math> oznacza liczbę oczek niezależnych. Podobnie jak w metodzie węzłowej liczba oczek jest zwykle dużo mniejsza niż liczba gałęzi obwodu, stąd metoda prądów oczkowych jest dużo bardziej efektywna niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa. | ||
|} | |} | ||
| Linia 423: | Linia 423: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd28.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd28.png|500px]] | ||
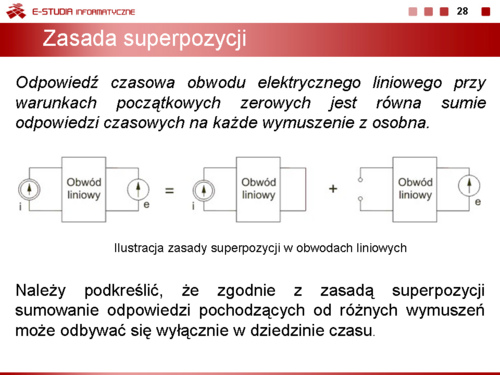
|valign="top"|'''Zasada superpozycji''' | |valign="top"|'''Zasada superpozycji''' | ||
Wersja z 10:22, 6 wrz 2006

|
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |

|
Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie
|
| Zadania sprawdzające
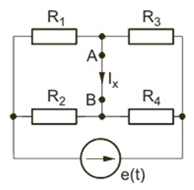
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , .
Impedancja z zacisków AB obwodu (rysunek a) jest równa
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
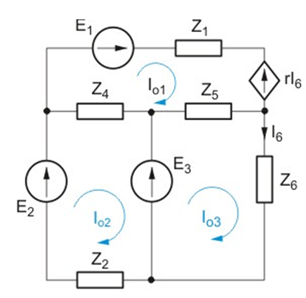
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci
|