Wersja z 19:29, 17 lip 2006

Wprowadzenie

Jeszcze nie ma...

Podstawowe przekształcenia poprawiające kod

Propagacja kopii

Instrukcja postaci X = Y jest instrukcją kopiowania. Naturalne jest zastąpienie wystąpień zmiennej X przez Y.

Przykład:

x = y
a = x + y
b = a + x

Zastępujemy przez:

x = y
a = y + y
b = a + y

Po wykonaniu propagacji kopii, instrukcja kopiująca jest martwym kodem. Ostatecznie otrzymamy:

a = y + y
b = a + y

Eliminacja wspólnych podwyrażeń

Wyrażenie E postaci X op Y jest nazywane wspólnym podwyrażeniem jeśli występuje ono w kilku miejscach oraz wartości zmiennych X i Y użytych w kolejnych wystąpieniach E nie zmieniły się po poprzednim obliczeniu E. W takiej sytuacji można zastąpić kolejne wystąpienia E przez wartość wyliczoną za pierwszym razem.

Przykład:

a = 4 * i
b = 4 * i
c = a + b

Drugie wyliczenie 4 * i można zastąpić przez b. Przekształcony blok:

a = 4 * i
b = a
c = a + b

Eliminację wspólnych podwyrażeń można stosować

lokalnie - gdy przeszukujemy jeden blok bazowy,
globalnie - dla całego grafu przepływu (trudniejsze z powodu pętli).

Usuwanie martwego kodu

Zmienną nazywamy żywą w danym miejscu programu, jeżeli jej wartość może zostać użyta. W pozostałych przypadkach nazywamy zmienną martwą w tym miejscu. Analogicznie definiujemy kod martwy, tzn. taki który oblicza wartości bezużyteczne. Na przykład wyliczenie wartości dla zmiennej martwej lub instrukcja postaci

if (false) ...

to kod martwy.

W oczywisty sposób kod martwy usuwamy.

Często kod martwy powstaje po propagacji kopii lub po zwijaniu stałych .

Zwijanie stałych

Jest to proces upraszczania wyrażeń stałych. Przykład:

x = 30 * 2

można zastąpić przez

x = 60

Zwijanie stałych czasem wykonuje się na wcześniejszych etapach kompilacji.

Propagacja stałych

Jest to proces zastępowania wystąpień stałych przez ich wartości. Przykład

x = 60
y = 3 * x

można zastąpić przez

x = 60
y = 3 * 60

i dalej po zwinięciu wartości w drugim przypisaniu otrzymamy

x = 60
y = 180

W wyniku propagacji stałych instrukcja definiująca stałą staje się martwym kodem, który można usunąć w trakcie eliminacji martwego kodu.

Optymalizacja pętli

Wstępniak!

Przemieszczenie kodu

Polega na zmiejszeniu ilości kodu w pętli, przez przemieszczenie obliczeń niezmienniczych przed pętle.

Prosty przykład:

i = 0
do {
   a = 13
   i = i + 1
} while (i < 15)

przedstawiamy w postaci SSA:

(0) i1 = 0
(1) i2 =  $ϕ$ (i1,i3)
(2) a = 13
(3) i3 = i2 + 1
(4) if (i3 < 15) goto (1)

Wyrażeniem niezmienniczym jest instrukcja przypisania w linii (2). Możemy ją przemieścić przed pętlę:

(0) i1 = 0
(1) a = 13
(2) i2 =  $ϕ$ (i1,i3)
(3) i3 = i2 + 1
(4) if (i3 < 15) goto (2)

W ogólnej sytuacji stosujemy schemat: jeśli I jest instrukcją X = Y op Z, oraz Y, Z nie odwołują się do $ϕ$ -węzła lub definicji wewnątrz pętli, wtedy

usuń instrukcję I (to jest instrukcja niezmiennicza dla tej pętli)
utwórz nową tymczasową zmienną T
wstaw nową instrukcję T = Y op Z oraz X = T do (ewentualnie nowego) bloku przed tą pętlą.

Proces ten rozszerzamy wykonując iteracyjnie:

jeśli argumenty operacji pewnej instrukcji są zdefiniowane przez instrukcje niezmiennicze (tzn. ta instrukcja jest również niezmiennicza w pętli), wykonuj analogiczne przenoszenie kodu do bloku przed pęltą.

Zmienne indukcyjne i redukcja mocy

Identyfikacja zmiennych, które zmieniają się w regularny sposób w pętli ułatwia optymalizacje pętli. Zmienne o takiej własności nazywany indukcyjnymi. W połączeniu z redukcją mocy (czyli zastępowaniem drogich obliczeń przez tańsze, np. zamiast mnożenia dodawanie), można w najlepszym przypadku zostawić tylko jedną zmienną indukcyjną.

Zmienne indukcyjne w poniższym przykładzie to i, j:

i = 0 
do { 
  j = 4 * i
  i = i + 1 
} while (i < 20)

Identyfikowanie zmiennych indukcyjnych jest prostsze gdy program jest w postaci SSA.

Zaczniemy od obliczenia zbioru kandydatów na zmienne indukcyjne: Dla danej pętli L, zmienna T jest kandydatem na zmienną indukcyjną dla L (niżej będziemy pisać jest kandydatem) wtedy i tylko wtedy gdy T jest obliczana w L i to obliczenie ma jedną następujących postaci:

T = X ± Y, gdzie jeden z argumentów jest kandydatem, a drugi jest niezmienniczy dla L.
T = X, gdzie X jest kandydatem lub niezmienniczy dla L.
T = ± X, gdzie X jest kandydatem dla L.
T = $ϕ$ (T1, . . ., Tm), gdzie każdy z argumentów jest albo kandydatem albo niezmienniczy dla L.

Zdefiniujemy teraz pojęcie zbioru indukcyjnego i zmiennych indukcyjnych. Rozważmy graf skierowany, którego wierzchołkami są kandydaci, a zbiór krawędzi posiada krawędź z T do U jeśli T jest użyta do obliczenia wartości U. Zmienna indukcyjna jest kandydatem, który jest elementem silnie spójnej składowej tego grafu. Zbiór zmiennych w takiej silnie spójnej składowej nazywamy zbiorem indukcyjnym.

Przykład:

m = 0 
do 
   l = m + 1
   t = l + 2
   m = t - 4
while (true)

Zapisujemy w postaci SSA:

(1) m $_{0}$  = 0
(2) m $_{1}$ =\phi(m $_{0}$ ,m $_{2}$ )
(3) l $_{1}$  = m $_{1}$  + 1
(4) t $_{1}$  = l $_{1}$  + 2
(5) m $_{2}$  = t $_{1}$  - 4
(6) goto (2)

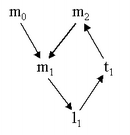
Graf skierowany dla kandydatów na zmienne indukcyjne jest przedstawiony poniżej:

Zbiorem indukcyjnym jest: {m $_{1}$ ,l $_{1}$ ,t $_{1}$ ,m $_{2}$ }. Zaczynamy od zmiennej m $_{1}$ definiowanej przez $ϕ$ i wartości pozostałych można przedstawić w postaci: m $_{1}$ + C, gdzie C jest stałą. Tu:

(1) m $_{0}$  = 0
(2) m $_{1}$ =\phi(m $_{0}$ ,m $_{2}$ )
(3) l $_{1}$  = m $_{1}$  + 1
(4) t $_{1}$  = m $_{1}$  + 3
(5) m $_{2}$  = m $_{1}$  - 1
(6) goto (2)

Po wykonaniu tej operacji zmienne l $_{1}$ , t $_{1}$ nie są używane do obliczania m $_{2}$ . Jest mniej zależności i być może część zmiennych będzie usunięta po zastosowaniu innych rodzajów optymalizacji.

W przypadku gdy do wyliczania używamy mnożenia, można zastosować inne podejście. Najpierw klasyfikujemy zmienne na kilka rodzajów:

Zmienna indukcyjna podstawowa - jej definicja występuje dokładnie raz w pętli i jest postaci i = i + C, gdzie C jest niezmiennicze w pętli.
Zmienna indukcyjna wspólna - jej definicja występuje dokładnie raz w pętli i jej wartość jest funkcją liniową pewnej zmiennej indukcyjnej; czyli i = A op j + B, gdzie A oraz B są niezmiennicze w pętli, op jest operatorem mnożenia lub dzielenia, a j jest zmienną indukcyjną.

Algorytm redukcji mocy: dla zmiennej indukcyjnej wspólnej $i$ zdefiniowanej przez i = A * j + B, gdzie j jest zmienną indukcyjną podstawową.

Stwórz nową zmienną k.
Dodaj przed pętlą k = A * j + B (przekształć do SSA).
Za instrukcją j = j + C dodaj k = k + B * C (przekształć do SSA).
Zastąp definicję i przez i = k.

Odniesione korzyści to mniejsza liczba operacji mnożenia oraz wyniesione przed pętle obliczenia na wartościach niezmienniczych A, B oraz C.

@@ Linia 6: / Linia 6: @@
 == Propagacja kopii ==
+{{kotwica|propagacjakopii|}}
-Instrukcja postaci <math>X = Y</math> jest instrukcją kopiowania.
+Instrukcja postaci ''X = Y'' jest instrukcją kopiowania.
-Naturalne jest zastąpienie wystąpień zmiennej <math>X</math> przez <math>Y</math>.
+Naturalne jest zastąpienie wystąpień zmiennej ''X'' przez ''Y''.
 Przykład:
@@ Linia 26: / Linia 26: @@
 == Eliminacja wspólnych podwyrażeń ==
-Wyrażenie <math>E</math> postaci <math>X\;op\;Y</math> jest nazywane '''wspólnym podwyrażeniem''' jeśli występuje ono w kilku miejscach oraz
+Wyrażenie ''E'' postaci ''X op Y'' jest nazywane '''wspólnym podwyrażeniem''' jeśli występuje ono w kilku miejscach oraz
-wartości zmiennych <math>X</math> i <math>Y</math> użytych w kolejnych wystąpieniach  <math>E</math> nie zmieniły się po poprzednim obliczeniu <math>E</math>. W takiej sytuacji można zastąpić
+wartości zmiennych ''X'' i ''Y'' użytych w kolejnych wystąpieniach  ''E'' nie zmieniły się po poprzednim obliczeniu ''E''. W takiej sytuacji można zastąpić
-kolejne wystąpienia <math>E</math> przez wartość wyliczoną za pierwszym razem.
+kolejne wystąpienia ''E'' przez wartość wyliczoną za pierwszym razem.
 Przykład:
@@ Linia 35: / Linia 35: @@
   c = a + b
-Drugie wyliczenie <math>4 * i</math> można zastąpić przez <math>b</math>. Przekształcony blok:
+Drugie wyliczenie ''4 * i'' można zastąpić przez ''b''. Przekształcony blok:
   a = 4 * i
   b = a
@@ Linia 92: / Linia 92: @@
   y = 180
-W wyniku propagacji stałych instrukcja definiująca stałą staje się martwym kodem,
+W wyniku propagacji stałych instrukcja definiująca stałą staje się [[Metody realizacji języków programowania/MRJP Wykład 8#martwykod|martwym kodem]],
 który można usunąć w trakcie eliminacji martwego kodu.
@@ Linia 101: / Linia 101: @@
 == Przemieszczenie kodu ==
-Polega na zmiejszeniu ilości kodu w pętli, przez przemieszczenie obliczeń niezmienniczych
+Polega na zmiejszeniu ilości kodu w pętli, przez przemieszczenie '''obliczeń niezmienniczych'''
 przed pętle.
@@ Linia 127: / Linia 127: @@
 W ogólnej sytuacji stosujemy schemat:
-jeśli <math>I</math> jest instrukcją <math>X = Y op Z</math>, oraz <math>Y</math>, <math>Z</math> nie odwołują się do <math>\phi</math>-węzła lub definicji wewnątrz pętli, wtedy
+jeśli ''I'' jest instrukcją ''X = Y op Z'', oraz ''Y'', ''Z'' nie odwołują się do <math>\phi</math>-węzła lub definicji wewnątrz pętli, wtedy
-* usuń instrukcję <math>I</math> (to jest instrukcja niezmiennicza dla tej pętli)
+* usuń instrukcję ''I'' (to jest instrukcja niezmiennicza dla tej pętli)
-* utwórz nową tymczasową zmienną <math>T</math>
+* utwórz nową tymczasową zmienną ''T''
-* wstaw nową instrukcję <math>T = Y op Z</math> oraz <math>X = T</math> do (ewentualnie nowego) bloku przed tą pętlą.
+* wstaw nową instrukcję ''T = Y op Z'' oraz ''X = T'' do (ewentualnie nowego) bloku przed tą pętlą.
 Proces ten rozszerzamy wykonując iteracyjnie:
@@ Linia 137: / Linia 137: @@
 == Zmienne indukcyjne i redukcja mocy==
-Identyfikacja zmiennych, które zmieniają się w regularny sposób w pętli ułatwia  optymalizacje pętli. Zmienne o takiej własności nazywany indukcyjnymi.
+Identyfikacja zmiennych, które zmieniają się w regularny sposób w pętli ułatwia  optymalizacje pętli. Zmienne o takiej własności nazywany '''indukcyjnymi'''.
-W połączeniu z redukcją mocy (czyli zastępowaniem drogich obliczeń przez tańsze, np. zamiast mnożenia dodawanie), można w najlepszym przypadku zostawić tylko jedną zmienną indukcyjną.
+W połączeniu z '''redukcją mocy''' (czyli zastępowaniem drogich obliczeń przez tańsze, np. zamiast mnożenia dodawanie), można w najlepszym przypadku zostawić tylko jedną zmienną indukcyjną.
-Zmienne indukcyjne w poniższym przykładzie to <math>i, j</math>:
+Zmienne indukcyjne w poniższym przykładzie to ''i, j'':
   i = 0
@@ Linia 151: / Linia 151: @@
 Zaczniemy od obliczenia zbioru '''kandydatów na zmienne indukcyjne''':
-Dla danej pętli <math>L</math>, zmienna <math>T</math> jest kandydatem na zmienną indukcyjną dla <math>L</math> (niżej będziemy pisać ''jest kandydatem'') wtedy i tylko wtedy gdy <math>T</math> jest obliczana w <math>L</math> i to obliczenie ma jedną następujących postaci:
+Dla danej pętli ''L'', zmienna ''T'' jest kandydatem na zmienną indukcyjną dla ''L'' (niżej będziemy pisać ''jest kandydatem'') wtedy i tylko wtedy gdy ''T'' jest obliczana w ''L'' i to obliczenie ma jedną następujących postaci:
-* <math>T = T_i</math> ± <math>T_j</math>, gdzie jeden z argumentów jest kandydatem, a drugi jest niezmienniczy dla <math>L</math>.
+* ''T = X ± Y'', gdzie jeden z argumentów jest kandydatem, a drugi jest niezmienniczy dla ''L''.
-* <math>T = T_k</math>, gdzie <math>T_k</math> jest kandydatem lub niezmienniczy dla <math>L</math>.
+* ''T = X'', gdzie ''X'' jest kandydatem lub niezmienniczy dla ''L''.
-* <math>T = </math> ± <math> T_k</math>, gdzie <math>T_k</math> jest kandydatem dla <math>L</math>.
+* ''T = ± X'', gdzie ''X'' jest kandydatem dla ''L''.
-* <math>T = \phi(T_1, . . ., T_m)</math>, gdzie każdy z argumentów jest albo kandydatem albo niezmienniczy dla <math>L</math>.
+* ''T = <math>\phi</math>(T1, . . ., Tm)'', gdzie każdy z argumentów jest albo kandydatem albo niezmienniczy dla ''L''.
 Zdefiniujemy teraz pojęcie '''zbioru indukcyjnego''' i '''zmiennych indukcyjnych'''.
@@ Linia 170: / Linia 170: @@
 Zapisujemy w postaci SSA:
-  (1) <math>m_0</math> = 0
+  (1) m<math>{}_0</math> = 0
-  (2) <math>m_1=\phi(m_0,m_2)</math>
+  (2) m<math>{}_1</math>=\phi(m<math>{}_0</math>,m<math>{}_2</math>)
-  (3) <math>l_1</math> = <math>m_1</math> + 1
+  (3) l<math>{}_1</math> = m<math>{}_1</math> + 1
-  (4) <math>t_1</math> = <math>l_1</math> + 2
+  (4) t<math>{}_1</math> = l<math>{}_1</math> + 2
-  (5) <math>m_2</math> = <math>t_1</math> - 4
+  (5) m<math>{}_2</math> = t<math>{}_1</math> - 4
   (6) '''goto''' (2)
@@ Linia 181: / Linia 181: @@
 [[Grafika:Mrjp8cykl.png]]
-Zbiorem indukcyjnym jest: <math>\{m_1,l_1,t_1,m_2\}</math>. Zaczynamy od zmiennej <math>m_1</math> definiowanej przez
+Zbiorem indukcyjnym jest: ''{m<math>{}_1</math>,l<math>{}_1</math>,t<math>{}_1</math>,m<math>{}_2</math>}''. Zaczynamy od zmiennej ''m<math>{}_1</math>'' definiowanej przez
-<math>\phi</math> i wartości pozostałych można przedstawić w postaci: <math>m_1 + C</math>, gdzie
+<math>\phi</math> i wartości pozostałych można przedstawić w postaci:
-<math>C</math> jest stałą. Tu:
+''m<math>{}_1</math> + C'', gdzie
+''C'' jest stałą. Tu:
-  (1) <math>m_0</math> = 0
+  (1) m<math>{}_0</math> = 0
-  (2) <math>m_1=\phi(m_0,m_2)</math>
+  (2) m<math>{}_1</math>=\phi(m<math>{}_0</math>,m<math>{}_2</math>)
-  (3) <math>l_1</math> = <math>m_1</math> + 1
+  (3) l<math>{}_1</math> = m<math>{}_1</math> + 1
-  (4) <math>t_1</math> = <math>m_1</math> + 3
+  (4) t<math>{}_1</math> = m<math>{}_1</math> + 3
-  (5) <math>m_2</math> = <math>m_1</math> - 1
+  (5) m<math>{}_2</math> = m<math>{}_1</math> - 1
   (6) '''goto''' (2)
-Po wykonaniu tej operacji zmienne <math>l_1</math>, <math>t_2</math> nie są używane do obliczania
+Po wykonaniu tej operacji zmienne ''l<math>{}_1</math>'', ''t<math>{}_1</math>'' nie są używane do obliczania
-<math>m_2</math>. Jest mniej zależności i być może część zmiennych będzie usunięta po zastosowaniu innych rodzajów optymaliazacji.
+''m<math>{}_2</math>''. Jest mniej zależności i być może część zmiennych będzie usunięta po zastosowaniu innych rodzajów optymalizacji.
 W przypadku gdy do wyliczania używamy mnożenia, można zastosować inne podejście.
-Tu klasyfikujemy zmienne na kilka rodzajów:
+Najpierw klasyfikujemy zmienne na kilka rodzajów:
-* '''Zmienna indukcyjna podstawowa''' - jej definicja występuje dokładnie raz w pętli i jest postaci  <math>i = i + C</math>, gdzie <math>C</math> jest niezmiennicze w pętli.
+* '''Zmienna indukcyjna podstawowa''' - jej definicja występuje dokładnie raz w pętli i jest postaci  ''i = i + C'', gdzie ''C'' jest niezmiennicze w pętli.
-* '''Zmienna indukcyjna wspólna''' - jej definicja występuje dokładnie raz w pętli i jej wartość jest funkcją liniową pewnej zmiennej indukcyjnej; czyli <math>i = j op C_1 + C_2</math>, gdzie <math>C_1</math> oraz <math>C_2</math> są niezmiennicze w pętli, <math>op</math> jest operatorem mnożenia lub dzieleniam, a <math>j</math> jest zmienną indukcyjną.
+* '''Zmienna indukcyjna wspólna''' - jej definicja występuje dokładnie raz w pętli i jej wartość jest funkcją liniową pewnej zmiennej indukcyjnej; czyli ''i = A op j + B'', gdzie ''A'' oraz ''B'' są niezmiennicze w pętli, ''op'' jest operatorem mnożenia lub dzielenia, a ''j'' jest zmienną indukcyjną.
-*
-'''Algorytm redukcji mocy''': dla zmiennej indukcyjnej wspólnej <math>i</math> zdefiniowanej przez <math>i = j * C_1 + C_2</math>, gdzie <math>j</math> jest zmienną indukcyjną podstawową.
+'''Algorytm redukcji mocy''': dla zmiennej indukcyjnej wspólnej <math>i</math> zdefiniowanej przez ''i = A * j + B'', gdzie ''j'' jest zmienną indukcyjną podstawową.
-# Stwórz nową zmienną <math>k</math>.
+# Stwórz nową zmienną ''k''.
-# Dodaj przed pętlą <math>k = j * C_1 + C_2</math> (przekształć do SSA).
+# Dodaj przed pętlą ''k = A * j + B'' (przekształć do SSA).
-# Za instrukcją <math>j = j + C_3</math> dodaj <math>k = k + C_1 * C_3</math> (przekształć do SSA).
+# Za instrukcją ''j = j + C'' dodaj ''k = k + B * C'' (przekształć do SSA).
-# Zastąp definicję <math>i</math> przez <math>i = k</math>.
+# Zastąp definicję ''i'' przez ''i = k''.
 Odniesione korzyści to  mniejsza liczba operacji mnożenia oraz wyniesione przed pętle obliczenia
-na wartościach niezmienniczych <math>C_1</math>, <math>C_2</math> oraz <math>C_3</math>.
+na wartościach niezmienniczych ''A'', ''B'' oraz ''C''.
-*

Metody realizacji języków programowania/MRJP Wykład 8: Różnice pomiędzy wersjami

Wersja z 19:29, 17 lip 2006

Spis treści

Wprowadzenie

Podstawowe przekształcenia poprawiające kod

Propagacja kopii

Eliminacja wspólnych podwyrażeń

Usuwanie martwego kodu

Zwijanie stałych

Propagacja stałych

Optymalizacja pętli

Przemieszczenie kodu

Zmienne indukcyjne i redukcja mocy

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia