SW wykład 4 - Slajd15

<<powrót do strony wykładu

Semantyka denotacyjna Dziedziny składniowe i semantyczne Funkcje semantyczne Kompozycjonalność Tiny. Semantyka denotacyjna Tiny. Semantyka denotacyjna, c.d. Pojęcia pomocnicze Pojęcia pomocnicze, c.d. |Tiny. Semantyka denotacyjna, c.d. Tiny. Semantyka denotacyjna, c.d. Problem z while Konstrukcje stałopunktowe Konstrukcje stałopunktowe, c.d. Konstrukcje stałopunktowe, c.d. Przykład Przykład, c.d. Dowód Dowód Zgodność semantyki denotacyjnej

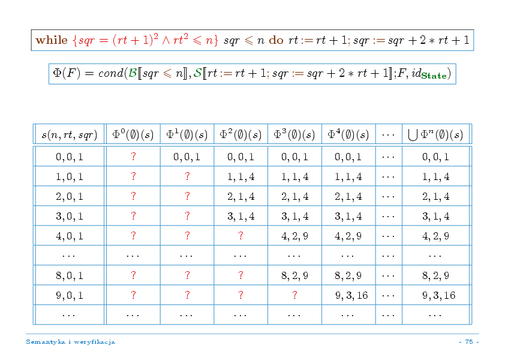
Spójrzmy jeszcze na przykład pętli z programu obliczającego całkowity pierwiastek kwadratowy liczby naturalnej (pierwsza ramka na slajdzie). Z pętlą tą wiążemy operator na dziedzinie semantycznej dla instrukcji zadany w drugiej ramce na slajdzie. Klauzula semantyczna dla instrukcji pętli przypisuje zatem tej pętli znaczenie, będące najmniejszym punktem stałym tego operatora. Zgodnie z powyższą analizą, jest to więc suma kolejnych iteracji tego operatora na funkcji pustej.

Tabela przedstawia wartości tych kolejnych iteracji dla interesujących nas stanów początkowych (patrz cały program przedstawiony na wykładzie wstępnym tych zajęć --- wykład 1, slajd 14). Stany opisujemy podając tylko trójki wartości interesujących nas zmiennych (wartości pozostałych zmiennych nie ulegają zmianie i nie mają wpływu na przebieg obliczeń pętli). Znak "?" oznacza, że wartość funkcji dla danego argumentu jest nieokreślona.

Koniecznie zwróćmy uwagę, że gdy na pewnym stanie któraś z iteracji operatora na funkcji pustej daje określony wynik, to wszystkie kolejne iteracje na tym stanie dają ten sam wynik.

Przykład ten potwierdza intuicyjne związki kolejnych iteracji operatora z obliczeniami pętli i liczbą wykonań ciała pętli niezbędnych do zakończenia obliczenia.