MN08: Różnice pomiędzy wersjami
mNie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
= | =Wielkie układy równań liniowych= | ||
Wraz z coraz większymi modelami pojawiającymi się w praktyce obliczeniowej, | |||
coraz częściej zachodzi potrzeba rozwiązywania zadań algebry liniowej, w której | |||
macierze są co prawda wielkiego wymiaru, ale najczęściej <strong>rozrzedzone</strong>, to | |||
znaczy jest w nich bardzo dużo zer. Bardzo często zdarza się, że macierz | |||
wymiaru <math>\displaystyle N</math> ma tylko <math>\displaystyle O(N)</math> niezerowych elementów. Wykorzytanie tej specyficznej | |||
własności macierzy nie tylko prowadzi do algorytmów istotnie szybszych od ich | |||
analogów dla macierzy gęstych (to znaczy takich, które (w założeniu) mają <math>\displaystyle N^2</math> | |||
elementów), ale wręcz są jedynym sposobem na to, by niektóre zadania w ogóle | |||
stały się rozwiązywalne przy obecnym stanie techniki obliczeniowej! | |||
Jednym ze szczególnie ważnych źródeł układów równań z macierzami rozrzedzonymi | |||
są np. '''równania różniczkowe cząstkowe''' (a więc np. modele pogody, naprężeń w | |||
konstrukcji samochodu, przenikania kosmetyków do głębszych warstw skóry, itp.). | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="font-variant:small-caps;">Przykład: Macierz z kolekcji Boeinga</span> | |||
<div class="solution"> | |||
Macierz sztywności dla modelu silnika lotniczego, wygenerowana swego czasu w | |||
zakładach Boeinga. Pochodzi z | |||
[http://www.cise.ufl.edu/research/sparse/matrices/Boeing kolekcji Tima | |||
Davisa] (autora bardzo dobrego solvera równań liniowych z macierzami rzadkimi). | |||
Jest to mała macierz, wymiaru 8032 (w kolekcji spotkasz równania z milionem i | |||
więcej | |||
niewiadomych). | |||
[[Image:MNsparseA.png|thumb|450px|center|Struktura niezerowych elementów macierzy bcsstk38.]] | |||
</div></div> | |||
Modele wielostanowych systemów kolejkowych (np. routera obsługującego wiele komputerów) także | |||
prowadzą do gigantycznych układów równań z macierzami rozrzedzonymi o | |||
specyficznej strukturze. | |||
Z reguły zadania liniowe wielkiego wymiaru będą miały strukturę macierzy | |||
rozrzedzonej, gdyż najczęściej związki pomiędzy niewiadomymi w równaniu nie | |||
dotyczą wszystkich, tylko wybranej grupy. | |||
< | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="font-variant:small-caps;">Przykład: Macierz MBEACXC</span> | |||
<div class="solution"> | |||
</ | |||
Dane pochodzą z serwisu | |||
[http://math.nist.gov/MatrixMarket MatrixMarket]. Jest to niezbyt duża macierz, wymiaru | |||
<math>\displaystyle 496 \times 496</math>, niesymetryczna, o elementach rzeczywistych. Źródłem tej | |||
macierzy jest pewien model ekonomiczny. | |||
<math>\displaystyle | |||
[[Image:MNmbeacxc|thumb|450px|center|Struktura niezerowych elementów macierzy MBEACXC]] | |||
Tylko pozornie macierz ta wydaje się dość gęsta, w rzeczywistości jej współczynnik wypełnienia | |||
wynosi około 20 procent. | |||
</div></div> | |||
==Formaty macierzy rzadkich== | |||
Zacznijmy od sposobu przechowywania macierzy rozrzedzonych. Naturalnie, nie ma | |||
sensu przechowywać wszystkich <strong>zerowych</strong> jej elementów: wystarczy | |||
ograniczyć się do zachowania tych niezerowych! W ten sposób zmniejszamy zarówno | |||
wymagania pamięciowe, jak i liczbę operacji zmiennoprzecinkowych potrzebnych do | |||
prowadzenia działań na macierzy (np. w przypadku mnożenia macierzy przez | |||
wektor, nie będziemy mnożyć przez zera!). | |||
====Format współrzędnych (AIJ)==== | |||
Do zapamiętania macierzy | |||
<math>\displaystyle A</math> wymiaru <math>\displaystyle N\times M</math> o <math>\displaystyle NNZ</math> niezerowych elementów, wykorzystujemy trzy wektory: <code>I</code>, | |||
<code>J</code> --- oba typu <code>int</code> --- oraz <code>V</code>, typu <code>double</code>, | |||
wszystkie o długości <math>\displaystyle NNZ</math>, przy czym | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
\ | A_{I[k], J[k]} = V[k], \qquad\forall k = 0,\ldots, NNZ-1. | ||
</math></center> | </math></center> | ||
[[Image:MNaij-matrix-format.png|thumb|450px|center|Format AIJ]] | |||
i | W tym formacie wprowadzane są macierze rzadkie do Octave'a i MATLABa: | ||
< | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
</ | A = sparse(I,J,V,N,N); | ||
</pre></div> | |||
====Format spakowanych kolumn (wierszy)==== | |||
Format współrzędnych nie narzucał żadnego uporządkowania elementów macierzy | |||
--- można było je umieszczać w dowolnej kolejności. Narzucenie sensownego | |||
porządku mogłoby wspomóc realizację wybranych istotnych operacji na macierzy, | |||
na przykład, aby wygodnie było realizować działanie (prawostronnego) mnożenia | |||
macierzy przez wektor, wygodnie byłoby przechowywać elementy macierzy <strong>wierszami</strong>. Tak właśnie jest zorganizowany format spakowanych wierszy, | |||
''Compressed Sparse Row (CSR) ''. Analogicznie jest zdefiniowany format | |||
spakowanych kolumn, | |||
''Compressed Sparse Column (CSC) '', którym zajmiemy się bliżej. | |||
Podobnie jak w przypadku formatu współrzędnych, macierz w formacie CSC jest | |||
przechowywana w postaci trzech wektorów: <code>AV</code> jest wektorem typu | |||
\ | <code>double</code> o długości <math>\displaystyle NNZ</math>, zawierającym <strong>kolejne</strong> niezerowe elementy | ||
macierzy <math>\displaystyle A</math> wpisywane <strong>kolumnami</strong>, <code>AI</code> jest wektorem typu <code>int</code> | |||
o długości <math>\displaystyle NNZ</math>, zawierającym numery wierszy macierzy <math>\displaystyle A</math>, odpowiadających | |||
elementom z <code>AV</code>. Natomiast zamiast tablicy <code>J</code>, jak to było w | |||
formacie współrzędnych, mamy krótszy wektor typu <code>int</code>, <code>AP</code>, o | |||
długości <math>\displaystyle M</math>, zawierający na <math>\displaystyle j</math>-tym miejscu indeks pozycji w <code>AV</code>, od | |||
którego rozpoczynają się w <code>AV</code> elementy <math>\displaystyle j</math>-tej kolumny macierzy <math>\displaystyle A</math>. | |||
[[Image:MNcsc-matrix-format.png|thumb|450px|center|Format CSC]] | |||
<center><math>\displaystyle | Mamy więc zależność, przy założeniu, że <math>\displaystyle AP[0]=0</math>, | ||
<center><math>\displaystyle | |||
A_{AI[AP[j]+k],j+1} = AV[AP[j]+k], \qquad j = 0,\ldots,M-1, \, k = | |||
\ | 0,\ldots,AP[j+1]-1. | ||
</math></center> | |||
Taki (z drobnymi modyfikacjami) format macierzy wykorzystują np. pakiety ARPACK | |||
i UMFPACK. | |||
====Format diagonalny==== | |||
{ | Znacznie mniej uniwersalny niż poprzednie i dlatego rzadziej spotykany. Kolejne | ||
< | diagonale macierzy przechowujemy w kolejnych wierszach macierzy <math>\displaystyle P\times N</math>, | ||
gdzie <math>\displaystyle P</math> jest liczbą niezerowych diagonal w <math>\displaystyle A\in R^{N\times N}</math>. | |||
Szczególnie wygodny do reprezentacji macierzy taśmowych. Wykorzystywany m.in. | |||
przez funkcję LAPACKa <code>DGBSV</code> służącą rozwiązywaniu równań z macierzami | |||
taśmowymi. | |||
== | ==Macierze specjalne== | ||
Zajmiemy się teraz zadaniem rozwiązywania układu równań liniowych | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
Ax = b, | |||
</math></center> | </math></center> | ||
ale w sytuacji, gdy macierz <math>\displaystyle A</math> jest rozrzedzona i dużego wymiaru. Dokonamy przeglądu kilku rodzajów algorytmów, mających na celu wykorzystanie rozrzedzenia macierzy dla obniżenia kosztu wyznaczenia rozwiązania układu. | |||
dla | Należy pamiętać, że z reguły najlepsze wyniki uzyskuje się, gdy konkretny | ||
algorytm dobierze się do konkretnej macierzy. W zastosowaniach pojawiają się | |||
m.in. macierze rzadkie o bardzo szczególnej strukturze, dla nich warto stosować | |||
wyspecjalizowane algorytmy. | |||
====Macierze taśmowe==== | |||
dla | Macierz <math>\displaystyle A</math> taka, że dla <math>\displaystyle |i-j| \geq d</math>, <math>\displaystyle a_{ij} = 0</math>, nazywamy macierzą taśmową | ||
z rozstępem <math>\displaystyle d</math>, o szerokości pasma <math>\displaystyle 2d+1</math>. | |||
Łatwo sprawdzić, że algorytm eliminacji Gaussa (bez wyboru elementu głównego) | |||
nie spowoduje dodatkowego wypełnienia w takiej macierzy (a więc da się wykonać w | |||
miejscu). W przypadku konieczności wyboru elementu głównego, pesymistyczne | |||
oszacowanie rozstępu macierzy rozkładu LU jest równe <math>\displaystyle \max\{2d,N\}</math> --- tak | |||
więc, dla niezbyt dużych <math>\displaystyle d</math> wciąż wynikowa macierz jest taśmowa. | |||
</math> | |||
W szczególności, gdy macierz jest taśmowa z pasmem o rozstępie <math>\displaystyle d</math> i jednocześnie | |||
diagonalnie dominująca, wtedy rozkład LU takiej macierzy da się wykonać w | |||
miejscu, kosztem <math>\displaystyle O(d\,N)</math>, czyli liniowym. | |||
W LAPACKu zaimplementowano szybki solver równań z macierzami taśmowymi, | |||
<code>DGBSV</code>, wymagający skądinąd specjalnego sposobu | |||
przechowywania macierzy, wykorzystyjącego format diagonalny. | |||
====Macierze trójdiagonalne==== | |||
= | Szczególnym przypadkiem macierzy taśmowych są macierze trójdiagonalne, tzn. taśmowe o | ||
rozstępie <math>\displaystyle d=1</math>: | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
A = | |||
\begin{pmatrix} | \begin{pmatrix} | ||
a_1 & c_1 & & & \\ | |||
b_2 & a_2 & c_2 & & \\ | |||
& b_3 & a_3 & \ddots & \\ | |||
& & \ddots & \ddots & c_{N-1}\\ | |||
\ | & & & b_N & a_N | ||
\end{pmatrix} | |||
</math></center> | </math></center> | ||
Zadanie rozwiązywania równań z taką macierzą | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
Ax = e | |||
</math></center> | </math></center> | ||
jest tak często spotykane, że | |||
warto przytoczyć algorytm w całej okazałości --- popularnie zwany algorytmem | |||
przeganiania. | |||
Zacznijmy jednak od stwierdzenia, kiedy taka macierz nie wymaga wyboru elementu | |||
głównego: | |||
{{stwierdzenie||| | |||
Jeśli macierz <math>\displaystyle A</math> ma <strong>słabo</strong> dominującą przekątną, tzn. | |||
<center><math>\displaystyle |a_i|\,\ge\,|b_i|\,+\,|c_i|,\qquad 1\le i\le N, | |||
<center><math>\displaystyle | |||
</math></center> | </math></center> | ||
(<math>\displaystyle b_1=0=c_N</math>) i przynajmniej dla jednego indeksu "<math>\displaystyle i</math>" mamy powyżej | |||
ostrą nierówność "<math>\displaystyle ></math>", to algorytm przeganiania jest wykonalny bez | |||
przestawień wierszy. Ponadto wymaga on <math>\displaystyle 7N</math> operacji arytmetycznych, | |||
a więc jest prawie optymalny. | |||
<math>\displaystyle | |||
}} | }} | ||
{{algorytm|Metoda przeganiania|| | |||
<pre> | |||
<math>\displaystyle d_1</math> = <math>\displaystyle a_1</math>; | |||
<math>\displaystyle f_1</math> = <math>\displaystyle e_1</math>; | |||
for (i = 2; i <= N; i++) | |||
<math>\displaystyle | { | ||
<math>\displaystyle l</math> = <math>\displaystyle b_i</math>/<math>\displaystyle a_{i-1}</math>; | |||
<math>\displaystyle d_i</math> = <math>\displaystyle a_i</math> - <math>\displaystyle l</math> * <math>\displaystyle c_{i-1}</math>; | |||
<math>\displaystyle f_i</math> = <math>\displaystyle e_i</math> - <math>\displaystyle l</math> * <math>\displaystyle f_{i-1}</math>; | |||
} | |||
<math>\displaystyle x_1</math> = <math>\displaystyle f_N</math>; | |||
for (i = N-1; i >= 1; i--) | |||
<math>\displaystyle x_i</math> = <math>\displaystyle f_i</math> - <math>\displaystyle c_i</math> * <math>\displaystyle x_{i+1}</math>; | |||
</pre>}} | |||
== | ==Metody bezpośrednie== | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="font-variant:small-caps;">Przykład: Strzałka Wilkinsona</span> | |||
<div class="solution"> | |||
Rozważmy układ równań z macierzą diagonalnie dominującą postaci | |||
<center><math>\displaystyle | <center><math>\displaystyle A = \begin{pmatrix} | ||
* & * & * & \cdots & * \\ | |||
* & * & & & \\ | |||
* & & * & & \\ | |||
\ | \vdots & & & \ddots & \\ | ||
* & & & & * | |||
\end{pmatrix} | |||
</math></center> | </math></center> | ||
gdzie <math>\displaystyle *</math> oznacza jakiś niezerowy element. | |||
Łatwo sprawdzić, że chociaż wyjściowa macierz jest rozrzedzona, to zastosowanie do niej eliminacji Gaussa powoduje, że w wyniku | |||
dostajemy <strong>gęste</strong> czynniki rozkładu. | |||
Tymczasem wystarczy odwrócić kolejność równań i numerację niewiadomych (co dla | |||
</math> | macierzy jest równoznaczne z odwróceniem porządku wierszy i kolumn, korzystając | ||
z pewnej (jakiej?) macierzy permutacji <math>\displaystyle P</math>): | |||
<center><math>\displaystyle \widetilde{A} = PAP^T = \begin{pmatrix} | |||
* & & & & *\\ | |||
& \ddots & & & \vdots\\ | |||
& & * & & * \\ | |||
& & & * & * \\ | |||
* & \cdots & * & * & * | |||
\end{pmatrix} | |||
\ | |||
</math></center> | </math></center> | ||
Wtedy okazuje się, że rozkład naszej macierzy nie powoduje już wypełnienia '' | |||
fill-in '' | |||
czynników rozkładu! | |||
</div></div> | |||
< | Właśnie na tym polega główny problem w rozwiązywaniu układów z macierzami | ||
rzadkimi metodami bezpośrednimi: maksymalnie wykorzystać rozrzedzenie macierzy | |||
tak, by czynniki rozkładu były możliwie mało wypełnione. Albowiem wiedząc to, | |||
będziemy mogli ograniczyć się jedynie do fizycznego wyznaczenia wartości <strong>niezerowych</strong> elementów macierzy rozkładu. Ponadto, wymagania pamięciowe | |||
algorytmu nie będą istotnie wykraczać ponad ilość pamięci potrzebnej na przechowanie | |||
danych (macierzy). | |||
W ogólnym przypadku rozwiązanie takiego zadania jest trudne i większość | |||
algorytmów opiera się na pewnych heurystykach, które warto wspomóc wcześniejszą | |||
analizą konkretnego układu równań, który mamy rozwiązać. Najczęściej dąży się do | |||
takiego przenumerowania równań i niewiadomych, by w efekcie z góry przewidzieć, | |||
gdzie wystąpią zera w macierzach rozkładu --- i, by takich zer było jak | |||
najwięcej (by wypełnienie było jak najmniejsze)! Na architekturach z pamięcią | |||
hierarchiczną dąży się także do tego, by w trakcie rozkładu można było korzystać | |||
z BLAS3, a więc permutacje wierszy i kolumn macierzy muszą to także brać pod | |||
uwagę (tzw. metody wielofrontowe). | |||
Stosuje się kilka strategii wyznaczania korzystnych permutacji | |||
''reorderingu '', z których warto wymienić | |||
* przybliżone algorytmy minimalnego stopnia ''approximate minimum degree ([http://www.cise.ufl.edu/research/sparse/amd AMD]) '' | |||
* techniki | |||
podziału grafów na (prawie) rozłączne składowe ([http://glaros.dtc.umn.edu/gkhome/views/metis METIS]). | |||
Używają ich biblioteki | |||
takie jak [http://www.cise.ufl.edu/research/sparse/umfpack UMFPACK], czy [http://www.cse.clrc.ac.uk/nag/hsl HSL]. | |||
W Octave mamy do dyspozycji także kilka procedur generujących takie permutacje, | |||
w tym: <code>colamd</code> (AMD dla macierzy niesymetrycznych) oraz <code>symamd</code> | |||
(AMD dla macierzy symetrycznych). Większy wybór oferuje MATLAB, jednak należy | |||
bezwzględnie pamiętać o jednym: nie ma uniwersalnej metody reorderingu i dla | |||
konkretnej macierzy może istnieć specjalna metoda, która da oszałamiające | |||
rezultaty, podczas gdy standardowe podejścia nie dadzą efektu. | |||
< | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="font-variant:small-caps;">Przykład: Wypełnienie pewnej macierzy w zależności od użytego algorytmu</span> | |||
</ | <div class="solution"> | ||
Rozważmy macierz pochodzącą z kolekcji | |||
[http://www.cise.ufl.edu/research/sparse/matrices/Boeing Tima Davisa], dotyczącą pewnego zadania | |||
mechaniki strukturalnej jakie pojawiło się u Boeinga. Jest to macierz | |||
symetryczna, dodatnio określona, wymiaru 8032. | |||
[[Image:MNsparseA.png|thumb|450px|center|Struktura niezerowych elementów macierzy.]] | |||
Jest to macierz silnie rozrzedzona, ponieważ ma tylko 355460 niezerowych | |||
elementów (czyli wypełnienie to tylko 0.5 procent). | |||
Zobaczymy, jak w zależności od użytego algorytmu permutacji kolumn i | |||
wierszy poradzi sobie algorytm rozkładu Cholesky'ego. | |||
[[Image:MNsparsechol.png|thumb|450px|center|Czynnik rozkładu Cholesky'ego <math>\displaystyle L</math> wykonanego | |||
standardowym algorytmem. Czas rozkładu: 0.892013]] | |||
[[Image:MNsparsecholcolamd.png|thumb|450px|center|Czynnik rozkładu Cholesky'ego <math>\displaystyle L</math> z reorderingiem | |||
COLAMD. Czas rozkładu: 0.813038]] | |||
[[Image:MNsparsecholsymamd.png|thumb|450px|center|Czynnik rozkładu Cholesky'ego <math>\displaystyle L</math> z reorderingiem | |||
</math> | SYMAMD. Czas rozkładu: 0.487683s. Prawie dwa razy | ||
szybciej niż bez reorderingu, chociaż i tak wskutek wzrostu wypełnienia macierzy | |||
w dolnym trójkącie mamy aż 2 procent niezerowych elementów.]] | |||
[[Image:MNsparsecholsymrcm.png|thumb|450px|center|Czynnik rozkładu Cholesky'ego <math>\displaystyle L</math> z odwrotnym reorderingiem | |||
Cuthill-McKee. Czas rozkładu: 0.845928]] | |||
[[Image:MNsparsecholcolperm.png|thumb|450px|center|Czynnik rozkładu Cholesky'ego <math>\displaystyle L</math> z jeszcze | |||
<math>\displaystyle | innym (bardzo tanim, ale jak widać czasem zupełnie złym) reorderingiem. Czas rozkładu: 5.947936]] | ||
Na zakończenie popatrzmy, jak ważne jest spostrzeżenie symetrii macierzy: | |||
[[Image:MNsparseLlu.png|thumb|450px|center|Rozkład LU, czynnik <math>\displaystyle L</math> (bez reorderingu). Czas rozkładu LU: 1.696018s. Nieakceptowalny, podobnie | |||
jak drastyczne wypełnienie macierzy.]] | |||
[[Image:MNsparseUlu.png|thumb|450px|center|Rozkład LU, czynnik <math>\displaystyle U</math> (bez reorderingu)]] | |||
</math> | |||
i | Jak widać, w naszym przypadku standardowe algorytmy (COLAMD i SYMAMD) poradziły sobie całkiem | ||
nieźle, chociaż wypełnienie i tak znacząco wzrosło. Zapewne algorytm oparty na | |||
podziale grafu na prawie rozłączne składowe mógłby tu jeszcze lepiej zadziałać. | |||
</div></div> | |||
</ | |||
==Stacjonarne metody iteracyjne== | |||
< | Gdy macierz jest rozrzedzona, mnożenie takiej macierzy przez wektor jest tanie | ||
(koszt jest proporcjonalny do liczby <strong>niezerowych</strong> elementów macierzy). | |||
Dlatego, jeśli możemy zadowolić się rozwiązaniem przybliżonym układu, a w zamian | |||
osiągnąć je tanim kosztem, warto rozważyć metody iteracyjne. | |||
Najprostsze metody iteracyjne (najprostsze w analizie i implementacji, ale --- | |||
jak można się domyślić --- w praktyce najmniej efektywne) polegają na rozkładzie | |||
macierzy na część "łatwo odwracalną", <math>\displaystyle M</math>, i "resztę", <math>\displaystyle Z</math>. Dokładniej, | |||
jeśli <math>\displaystyle M</math> jest nieosobliwa, to równanie <math>\displaystyle Ax = b</math> można zapisać jako | |||
zadanie punktu stałego | |||
<center><math>\displaystyle | <center><math>\displaystyle Mx = Nx + b, | ||
</math></center> | </math></center> | ||
gdzie <math>\displaystyle Z=M-A</math>. Inaczej: | |||
<center><math>\displaystyle x = M^{-1}(Zx + b), | |||
<center><math>\displaystyle | |||
</math></center> | </math></center> | ||
i zastosować doń [[sec:nieliniowe|Dodaj link: metodę iteracji prostej Banacha]]: | |||
<center><math>\displaystyle x_{k+1} = M^{-1}(Zx_k + b). | |||
</math></center> | </math></center> | ||
Takie metody nazywamy stacjonarnymi metodami iteracyjnymi. | |||
Aby przeanalizować zbieżność takiej metody, warto rozpatrzyć | |||
przypadek ogólniejszy | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
x_k\,=\,B x_{k-1}\,+\, c, | |||
</math></center> | </math></center> | ||
dla pewnej macierzy <math>\displaystyle B</math> wektora | |||
<math>\displaystyle c</math> (dla stacjonarnej metody iteracyjnej, <math>\displaystyle B=M^{-1}Z</math> oraz <math>\displaystyle c=M^{-1}b</math>). | |||
< | |||
</math> | |||
W tym przypadku | |||
<center><math>\displaystyle | <center><math>\displaystyle x_k- x^*\,=\,B^k( x_0- x^*), | ||
</math></center> | </math></center> | ||
a stąd i z nierówności <math>\displaystyle \|B^k\|\le\|B\|^k</math>, mamy | |||
<center><math>\displaystyle | <center><math>\displaystyle \| x_k- x^*\|\,\le\, | ||
\|B\|^k\| x_0- x^*\|. | |||
</math></center> | </math></center> | ||
Warunkiem dostatecznym zbieżności iteracji prostych | |||
jest więc <math>\displaystyle \|B\|<1</math>. Okazuje się, że warunkiem koniecznym i dostatecznym | |||
zbieżności tej iteracji dla dowolnego wektora startowego <math>\displaystyle x_0</math> jest | |||
<center><math>\displaystyle | <center><math>\displaystyle \rho = \max\{ |\lambda| : \lambda \mbox{ jest wartością własną } A\} < 1. | ||
</math></center> | </math></center> | ||
Tak więc, metody oparte na iteracji prostej, będą zbieżne liniowo z ilorazem | |||
<math>\displaystyle \rho</math>. | |||
</math> | |||
====Metoda Jacobiego==== | |||
< | [[grafika:Jacobi.jpg|thumb|right|| Jacobi<br> [[Biografia Jacobi|Zobacz biografię]]]] | ||
gdzie <math>\displaystyle | Biorąc <math>\displaystyle D = diag(A)</math> | ||
gdzie <math>\displaystyle diag(A)</math> jest macierzą diagonalną składającą się | |||
z wyrazów stojących na głównej przekątnej macierzy | |||
<math>\displaystyle A</math>, układ <math>\displaystyle A x= b</math> jest równoważny układowi | |||
<center><math>\displaystyle | <center><math>\displaystyle D x = Z x + b, | ||
</math></center> | </math></center> | ||
a stąd (o ile na przekątnej macierzy <math>\displaystyle A</math> nie mamy zera) | |||
otrzymujemy metodę iteracyjną | |||
<center><math>\displaystyle | <center><math>\displaystyle x_k\,=\,B x_{k-1}\,+\, c, | ||
</math></center> | </math></center> | ||
gdzie <math>\displaystyle B=-D^{-1}Z</math> i <math>\displaystyle c=D^{-1} b</math>, zwaną | |||
<strong>metodą Jacobiego</strong>. | |||
< | |||
<math>\displaystyle | W metodzie Jacobiego warunek dostateczny zbieżności, | ||
<math>\displaystyle \|B\|<1</math>, jest spełniony np. wtedy, gdy macierz <math>\displaystyle A</math> ma | |||
dominującą przekątną, tzn. gdy | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
|a_{i,i}|\,>\,\sum_{j\neq i}|a_{i,j}|,\qquad \forall i = 1,\ldots, N. | |||
</math></center> | </math></center> | ||
Rzeczywiście, ponieważ wyraz <math>\displaystyle (i,j)</math> macierzy <math>\displaystyle D^{-1}Z</math> | |||
wynosi <math>\displaystyle 0</math> dla <math>\displaystyle i=j</math> oraz <math>\displaystyle a_{i,j}/a_{i,i}</math> dla <math>\displaystyle i\neq j</math>, a więc | |||
<center><math>\displaystyle \aligned | <center><math>\displaystyle \aligned \lefteqn{\|D^{-1}Z\|_\infty \;=\; \max_{1\le i\le N} | ||
\sum_{j=1,j\ne i}^N{|a_{i,j}|}/{|a_{i,i}|} } \\ | |||
&& =\;\max_{1\le i\le N} | |||
\sum_{j=1}^N{|a_{i,j}|}/{|a_{i,i}|}\,-\,1\;<\;1, | |||
\endaligned</math></center> | \endaligned</math></center> | ||
przy czym ostatnia nierówność wynika z warunku diagonalnej dominacji. | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="font-variant:small-caps;">Przykład: Macierz laplasjanu</span> | |||
<div class="solution"> | |||
Macierz <math>\displaystyle N\times N</math>, zwana <strong>macierzą jednowymiarowego laplasjanu</strong> | |||
<center><math>\displaystyle | |||
L = \begin{pmatrix} | |||
2 & -1 & & \\ | |||
-1 & 2 & \ddots & \\ | |||
& \ddots & \ddots & -1 \\ | |||
& & -1 & 2 | |||
\end{pmatrix} | |||
</math></center> | |||
pojawia się w bardzo wielu zastosowaniach, także jako podzadanie w algorytmach | |||
numerycznych. Ta macierz jest macierzą taśmową, symetryczną i dodatnio | |||
okresloną, więc rozwiązanie układu równań z tą macierzą jest łatwe metodami | |||
bezpośrednimi, kosztem <math>\displaystyle O(N)</math>. Ciekawe będzie, jak poradzą sobie z nią metody | |||
iteracyjne. | |||
< | Na przykład, w metodzie Jacobiego weźmiemy <math>\displaystyle D = 2I</math> oraz <math>\displaystyle Z = L - D</math>. Obliczając | ||
normę macierzy iteracji Jacobiego dostajemy <math>\displaystyle ||D^{-1}Z||_\infty | |||
</math> | = 1</math>, co nie rozstrzyga jeszcze o jej (nie)zbieżności. | ||
Okazuje się, że są gotowe wzory na wartości własne macierzy <math>\displaystyle L</math>: | |||
<math>\displaystyle | |||
<center><math>\displaystyle \ | <center><math>\displaystyle \lambda_j = 4\sin^2 \left(\frac{j \pi }{2(N+1)} \right), | ||
</math></center> | </math></center> | ||
dla <math>\displaystyle 1 \leq j \leq N.</math> | |||
{{ | i w konsekwencji, wartościami własnymi <math>\displaystyle D^{-1}Z = \frac{1}{2}Z = \frac{1}{2}L - | ||
I</math> są liczby <math>\displaystyle \mu_i = \frac{1}{2} \lambda_i - 1</math>. Ponieważ <math>\displaystyle 0 < \mu_i < 1</math>, oraz <math>\displaystyle ||Z||_2 = 1 - O(N^{-2}) < 0</math> to metoda, choć zbieżna, dla dużych <math>\displaystyle N</math> staje się | |||
zbieżna tak wolno, że w praktyce bezużyteczna. | |||
</div></div> | |||
Zaletą stacjonarnych metod iteracyjnych jest również ich prostota, | |||
przez co są one łatwe do zaprogramowania. | |||
====Metoda Gaussa--Seidela==== | |||
Ciekawostką jest, że Gauss nie miał z nią nic wspólnego, a Seidel był wręcz jej | |||
przeciwnikiem... | |||
====Złożoność stacjonarnych metod iteracyjnych==== | |||
< | Zastanówmy się teraz nad złożonością metod | ||
iteracyjnych. Ponieważ możemy jedynie znaleźć pewne | |||
przybliżenie rozwiązania dokładnego <math>\displaystyle x^*</math>, przez | |||
złożoność metody będziemy rozumieli koszt | |||
kombinatoryczny obliczenia <math>\displaystyle x_k</math> z zadaną | |||
dokładnością <math>\displaystyle \epsilon>0</math>. Dla uproszczenia założymy, | |||
że medoda jest zbieżna liniowo z ilorazem <math>\displaystyle \rho</math>. | |||
Zauważmy, że aby zredukować błąd początkowy do | |||
<math>\displaystyle \epsilon>0</math>, wystarczy wykonać <math>\displaystyle k=k(\epsilon)</math> iteracji, gdzie | |||
<math>\displaystyle k</math> spełnia | |||
<center><math>\displaystyle \rho^k\| x_0- x^*\|\,\le\,\epsilon, | |||
</math></center> | |||
czyli | |||
<center><math>\displaystyle k\,\ge\,\frac{\log(1/\epsilon)- | |||
\log(1/\| x_0- x^*\|)}{\log(1/\rho)}. | |||
<center><math>\displaystyle | |||
</math></center> | </math></center> | ||
Liczba ta zależy więc w istotny sposób od błędu | |||
początkowego i (przede wszystkim) od współczynnika redukcji błędu | |||
<math>\displaystyle \rho</math>, natomiast zależność od dokładności <math>\displaystyle \epsilon</math> | |||
i wymiaru <math>\displaystyle N</math> układu jest dużo mniej istotna (w zadaniach praktycznych -- takich jak jednowymiarowy laplasjan --- jednak | |||
często | |||
się | okazuje się, że... <math>\displaystyle \rho</math> zależy od <math>\displaystyle N</math>!). | ||
Zakładając, że koszt jednej iteracji wynosi <math>\displaystyle c=c(N)</math> | |||
(<math>\displaystyle c(N)</math> jest tym mniejszy, im mniejsza jest liczba | |||
niezerowych elementów macierzy <math>\displaystyle A</math>), złożoność | |||
metody jest proporcjonalna do | |||
<center><math>\displaystyle | <center><math>\displaystyle c(N)\,\frac{\log(1/\epsilon)}{\log(1/\rho)}. | ||
</math></center> | </math></center> | ||
Stąd oczywisty wniosek, że metody iteracyjne warto | |||
stosować zamiast metod bezpośrednich w przypadku gdy | |||
* wymiar <math>\displaystyle N</math> układu <math>\displaystyle A x= b</math> jest "duży", oraz | |||
* macierz <math>\displaystyle A</math> układu jest "rozrzedzona", tzn. ma stosunkowo niewielką liczbę elementów niezerowych, np. proporcjonalną do <math>\displaystyle N</math>. | |||
Układy o tych własnościach powstają często przy | |||
numerycznym rozwiązywaniu równań różniczkowych | |||
cząstkowych. | |||
==Metody przestrzeni Kryłowa== | |||
Zupełnie inny pomysł na realizację metody iteracyjnej przedstawiają metody przestrzeni | |||
Kryłowa, gdzie kolejne przybliżenie <math>\displaystyle x_k</math> dobiera się w taki sposób by | |||
minimalizowało pewną miarę błędu na podprzestrzeni Kryłowa | |||
<center><math>\displaystyle \ | <center><math>\displaystyle K_k = \mbox{span} \{r,A_r,\ldots, A^{k-1}r \}, | ||
</math></center> | </math></center> | ||
gdzie <math>\displaystyle r = b-Ax_0</math> jest residuum na początku iteracji. W zależności od wyboru | |||
sposobu miary błędu, dostajemy inną metodę iteracyjną, takie jak CG, GMRES, PCR, | |||
BiCG, i inne. Tutaj omówimy pokrótce tylko dwie najpopularniejsze: CG i GMRES. | |||
====CG==== | |||
Metoda <strong>gradientów sprzężonych</strong> ''conjugate gradients (CG) ''działa przy założeniu, że <math>\displaystyle A</math> jest <strong>symetryczna i dodatnio określona</strong>. | |||
Kolejne przybliżenie <math>\displaystyle x_k</math> ma minimalizować błąd w normie energetycznej | |||
indukowanej przez <math>\displaystyle A</math>, | |||
<center><math>\displaystyle | <center><math>\displaystyle ||x_k -x||_A = \sqrt{(x_k -x)^TA(x_k -x)} | ||
</math></center> | </math></center> | ||
na przestrzeni afinicznej <math>\displaystyle x_0 + K_k</math>. Okazuje się (co ''nie jest'' oczywiste --- trzeba skorzystać z rozmaitych własności ortogonalności generowanych wektorów), że takie zadanie minimalizacji daje się bardzo efektywnie rozwiązać, skąd dostajemy bardzo zwarty algorytm: | |||
{{ | {{algorytm||| | ||
<pre> | |||
r = b-A*x; | |||
<math>\displaystyle \rho_{-1}</math> = 0; <math>\displaystyle \rho_0</math> = <math>\displaystyle ||r||_2^2</math>; <math>\displaystyle \beta</math> = 0; k = 1; | |||
while <math>\displaystyle \sim</math>STOP | |||
{ | |||
<math>\displaystyle | p = r + <math>\displaystyle \beta</math>*p; | ||
w = A*p; | |||
< | <math>\displaystyle \alpha</math> = <math>\displaystyle \frac{\rho_{k-1}}{p^Tw}</math>; | ||
x = x + <math>\displaystyle \alpha</math>*p; | |||
r = r - <math>\displaystyle \alpha</math>*w; | |||
</math> | <math>\displaystyle \rho_k</math> = <math>\displaystyle ||r||_2^2</math>; | ||
<math>\displaystyle \beta</math> = <math>\displaystyle \frac{\rho_{k}}{\rho_{k-1}}</math>; | |||
k++; | |||
} | |||
w | </pre>}} | ||
</math></ | |||
a | Jak widać, całą iterację da się wykonać przechowując w pamięci tylko kilka wektorów (a nie, jak możnaby się obawiać, całą przestrzeń <math>\displaystyle K_k</math>), a najdroższym jej elementem jest mnożenie macierzy przez wektor. | ||
{{twierdzenie|Zbieżność CG jako metody bezpośredniej|| | |||
Niech <math>\displaystyle A\in R^{N\times N}</math> będzie symetryczna i dodatnio określona. Algorytm CG znajdzie dokładne rozwiązanie po co najwyżej <math>\displaystyle N</math> iteracjach. | |||
}} | }} | ||
Powyższe twierdzenie, choć teoretycznie interesujące, ma małą wartość praktyczną z dwóch powodów: | |||
* dla bardzo dużych <math>\displaystyle N</math>, wykonanie <math>\displaystyle N</math> iteracji może być wciąż zbyt kosztownym zadaniem | |||
* ponieważ w arytmetyce <math>\displaystyle fl_\nu</math> skończonej precyzji ortogonalność z której korzysta się przy wyprowadzeniu algorytmu nie jest zachowana i w konsekwencji, po wielu iteracjach, jakość <math>\displaystyle x_k</math> przestaje się poprawiać. | |||
<math>\displaystyle \ | |||
Dlatego wygodniej potraktować CG jako metodę iteracyjną. Zachodzi bowiem | |||
{{twierdzenie|Zbieżność CG jako metody iteracyjnej|| | |||
Po <math>\displaystyle k</math> iteracjach metody CG, | |||
<center><math>\displaystyle | <center><math>\displaystyle ||x_k - x||_A \leq 2 \, \left( \frac{\sqrt{ \mbox{cond} (A)} - 1}{\sqrt{ \mbox{cond} (A)} +1}\right)^k \, ||x_0 - x||_A, | ||
</math></center> | </math></center> | ||
gdzie <math>\displaystyle \mbox{cond} (A) = ||A||_2||A^{-1}||_2</math>. | |||
}} | }} | ||
Metoda GMRES ''Generalized Minimum RESidual ''nie wymaga ani symetrii, ani dodatniej określoności macierzy, jest więc bardziej uniwersalna, choć też bardziej kosztowna od CG. | |||
====Prekondycjoning==== | |||
Zbieżność wszystkich poznanych metod iteracyjnych zależu od własności | |||
spektralnych macierzy układu. Często w zastosowaniach pojawiające się macierze | |||
mają niekorzystne własności spektralne (np. bardzo duży wskaźnik uwarunkowania) | |||
przez co metody iteracyjne zbiegają na nich bardzo wolno. | |||
Dlatego bardzo korzystne może być wstępne przetransformowanie układu | |||
<center><math>\displaystyle Ax = b | |||
<center><math>\displaystyle | |||
</math></center> | </math></center> | ||
z macierzą o niekorzystnych własnościach, do układu | |||
<center><math>\displaystyle | <center><math>\displaystyle MAx = Mb, | ||
</math></center> | </math></center> | ||
gdzie macierz <math>\displaystyle MA</math> ma znacznie korzystniejsze własności z punktu widzenia | |||
używanej metody | |||
iteracyjnej. | |||
Taką operację nazywamy <strong>prekondycjoningiem</strong>, a macierz <math>\displaystyle M</math> --- macierzą | |||
prekondycjonera. | |||
< | Aby całość miała sens, macierz prekondycjonera <math>\displaystyle M</math> powinna: | ||
< | * być łatwa w konstrukcji, | ||
* być tania w mnożeniu przez wektor (głównym elementem każdej metody | |||
iteracyjnej jest mnożenie macierzy przez wektor: <math>\displaystyle M\cdot (A \cdot x)</math>), | |||
* macierz <math>\displaystyle MA</math> powinna mieć znacznie korzystniejsze własności z punktu widzenia | |||
używanej metody | |||
iteracyjnej. | |||
Kilka ekstremalnych propozycji na macierz prekondycjonera to <math>\displaystyle M = I</math> (łatwa w | |||
konstrukcji i tania w mnożeniu, ale nic nie polepsza, niestety...) oraz | |||
<math>\displaystyle M=A^{-1}</math> (rewelacyjnie poprawia zbieżność metody iteracyjnej, dając zbieżność | |||
w jednej iteracji, ale bardzo droga w konstrukcji i mnożeniu). Widać więc, że | |||
należy poszukiwać czegoś pośredniego, co niskim kosztem przybliża działanie | |||
macierzy odwrotnej. | |||
Dlatego jednym z powszechniej stosowanych rodzajów prekondycjonerów są oparte na | |||
zastosowaniu jednego kroku klasycznej metody iteracyjnej. | |||
[[Image:MNpcgconv.png|thumb|450px|center|Zbieżność metody CG bez prekondycjonera oraz z prekondycjonerem | |||
opartym na jednej iteracji (blokowej) metody Jacobiego.]] | |||
Inne prekondycjonery stosują np. techniki tzw. niepełnego rozkładu macierzy, | |||
w | albo --- w specyficznych przypadkach --- tzw. metody wielosiatkowe. | ||
Okazuje się, że zarówno CG jak i GMRES da się zaimplementować tak, by w jednej | |||
iteracji było konieczne tylko jedno mnożenie przez macierz prekondycjonera. | |||
Wersja z 18:25, 1 wrz 2006
Wielkie układy równań liniowych
Wraz z coraz większymi modelami pojawiającymi się w praktyce obliczeniowej, coraz częściej zachodzi potrzeba rozwiązywania zadań algebry liniowej, w której macierze są co prawda wielkiego wymiaru, ale najczęściej rozrzedzone, to znaczy jest w nich bardzo dużo zer. Bardzo często zdarza się, że macierz wymiaru ma tylko niezerowych elementów. Wykorzytanie tej specyficznej własności macierzy nie tylko prowadzi do algorytmów istotnie szybszych od ich analogów dla macierzy gęstych (to znaczy takich, które (w założeniu) mają elementów), ale wręcz są jedynym sposobem na to, by niektóre zadania w ogóle stały się rozwiązywalne przy obecnym stanie techniki obliczeniowej!
Jednym ze szczególnie ważnych źródeł układów równań z macierzami rozrzedzonymi są np. równania różniczkowe cząstkowe (a więc np. modele pogody, naprężeń w konstrukcji samochodu, przenikania kosmetyków do głębszych warstw skóry, itp.).
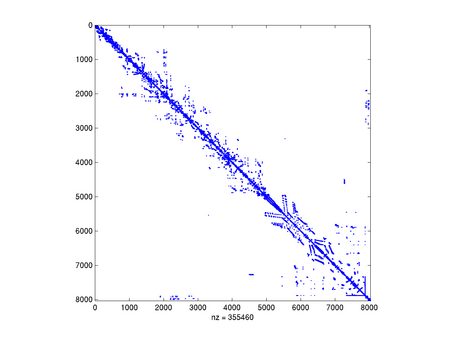
Przykład: Macierz z kolekcji Boeinga
Macierz sztywności dla modelu silnika lotniczego, wygenerowana swego czasu w zakładach Boeinga. Pochodzi z [http://www.cise.ufl.edu/research/sparse/matrices/Boeing kolekcji Tima Davisa] (autora bardzo dobrego solvera równań liniowych z macierzami rzadkimi). Jest to mała macierz, wymiaru 8032 (w kolekcji spotkasz równania z milionem i więcej niewiadomych).
Modele wielostanowych systemów kolejkowych (np. routera obsługującego wiele komputerów) także prowadzą do gigantycznych układów równań z macierzami rozrzedzonymi o specyficznej strukturze.
Z reguły zadania liniowe wielkiego wymiaru będą miały strukturę macierzy rozrzedzonej, gdyż najczęściej związki pomiędzy niewiadomymi w równaniu nie dotyczą wszystkich, tylko wybranej grupy.
Przykład: Macierz MBEACXC
Dane pochodzą z serwisu MatrixMarket. Jest to niezbyt duża macierz, wymiaru , niesymetryczna, o elementach rzeczywistych. Źródłem tej macierzy jest pewien model ekonomiczny.

Tylko pozornie macierz ta wydaje się dość gęsta, w rzeczywistości jej współczynnik wypełnienia wynosi około 20 procent.
Formaty macierzy rzadkich
Zacznijmy od sposobu przechowywania macierzy rozrzedzonych. Naturalnie, nie ma sensu przechowywać wszystkich zerowych jej elementów: wystarczy ograniczyć się do zachowania tych niezerowych! W ten sposób zmniejszamy zarówno wymagania pamięciowe, jak i liczbę operacji zmiennoprzecinkowych potrzebnych do prowadzenia działań na macierzy (np. w przypadku mnożenia macierzy przez wektor, nie będziemy mnożyć przez zera!).
Format współrzędnych (AIJ)
Do zapamiętania macierzy
wymiaru o niezerowych elementów, wykorzystujemy trzy wektory: I,
J --- oba typu int --- oraz V, typu double,
wszystkie o długości , przy czym

W tym formacie wprowadzane są macierze rzadkie do Octave'a i MATLABa:
A = sparse(I,J,V,N,N);
Format spakowanych kolumn (wierszy)
Format współrzędnych nie narzucał żadnego uporządkowania elementów macierzy --- można było je umieszczać w dowolnej kolejności. Narzucenie sensownego porządku mogłoby wspomóc realizację wybranych istotnych operacji na macierzy, na przykład, aby wygodnie było realizować działanie (prawostronnego) mnożenia macierzy przez wektor, wygodnie byłoby przechowywać elementy macierzy wierszami. Tak właśnie jest zorganizowany format spakowanych wierszy, Compressed Sparse Row (CSR) . Analogicznie jest zdefiniowany format spakowanych kolumn, Compressed Sparse Column (CSC) , którym zajmiemy się bliżej.
Podobnie jak w przypadku formatu współrzędnych, macierz w formacie CSC jest
przechowywana w postaci trzech wektorów: AV jest wektorem typu
double o długości , zawierającym kolejne niezerowe elementy
macierzy wpisywane kolumnami, AI jest wektorem typu int
o długości , zawierającym numery wierszy macierzy , odpowiadających
elementom z AV. Natomiast zamiast tablicy J, jak to było w
formacie współrzędnych, mamy krótszy wektor typu int, AP, o
długości , zawierający na -tym miejscu indeks pozycji w AV, od
którego rozpoczynają się w AV elementy -tej kolumny macierzy .
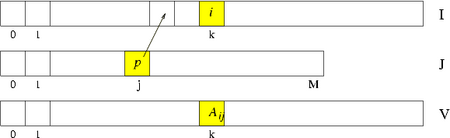
Mamy więc zależność, przy założeniu, że ,
Taki (z drobnymi modyfikacjami) format macierzy wykorzystują np. pakiety ARPACK i UMFPACK.
Format diagonalny
Znacznie mniej uniwersalny niż poprzednie i dlatego rzadziej spotykany. Kolejne diagonale macierzy przechowujemy w kolejnych wierszach macierzy , gdzie jest liczbą niezerowych diagonal w .
Szczególnie wygodny do reprezentacji macierzy taśmowych. Wykorzystywany m.in.
przez funkcję LAPACKa DGBSV służącą rozwiązywaniu równań z macierzami
taśmowymi.
Macierze specjalne
Zajmiemy się teraz zadaniem rozwiązywania układu równań liniowych
ale w sytuacji, gdy macierz jest rozrzedzona i dużego wymiaru. Dokonamy przeglądu kilku rodzajów algorytmów, mających na celu wykorzystanie rozrzedzenia macierzy dla obniżenia kosztu wyznaczenia rozwiązania układu.
Należy pamiętać, że z reguły najlepsze wyniki uzyskuje się, gdy konkretny algorytm dobierze się do konkretnej macierzy. W zastosowaniach pojawiają się m.in. macierze rzadkie o bardzo szczególnej strukturze, dla nich warto stosować wyspecjalizowane algorytmy.
Macierze taśmowe
Macierz taka, że dla , , nazywamy macierzą taśmową z rozstępem , o szerokości pasma .
Łatwo sprawdzić, że algorytm eliminacji Gaussa (bez wyboru elementu głównego) nie spowoduje dodatkowego wypełnienia w takiej macierzy (a więc da się wykonać w miejscu). W przypadku konieczności wyboru elementu głównego, pesymistyczne oszacowanie rozstępu macierzy rozkładu LU jest równe --- tak więc, dla niezbyt dużych wciąż wynikowa macierz jest taśmowa.
W szczególności, gdy macierz jest taśmowa z pasmem o rozstępie i jednocześnie diagonalnie dominująca, wtedy rozkład LU takiej macierzy da się wykonać w miejscu, kosztem , czyli liniowym.
W LAPACKu zaimplementowano szybki solver równań z macierzami taśmowymi,
DGBSV, wymagający skądinąd specjalnego sposobu
przechowywania macierzy, wykorzystyjącego format diagonalny.
Macierze trójdiagonalne
Szczególnym przypadkiem macierzy taśmowych są macierze trójdiagonalne, tzn. taśmowe o rozstępie :
Zadanie rozwiązywania równań z taką macierzą
jest tak często spotykane, że warto przytoczyć algorytm w całej okazałości --- popularnie zwany algorytmem przeganiania.
Zacznijmy jednak od stwierdzenia, kiedy taka macierz nie wymaga wyboru elementu głównego:
Stwierdzenie
Jeśli macierz ma słabo dominującą przekątną, tzn.
() i przynajmniej dla jednego indeksu "" mamy powyżej ostrą nierówność "", to algorytm przeganiania jest wykonalny bez przestawień wierszy. Ponadto wymaga on operacji arytmetycznych, a więc jest prawie optymalny.
Algorytm Metoda przeganiania
<math>\displaystyle d_1</math> = <math>\displaystyle a_1</math>;
<math>\displaystyle f_1</math> = <math>\displaystyle e_1</math>;
for (i = 2; i <= N; i++)
{
<math>\displaystyle l</math> = <math>\displaystyle b_i</math>/<math>\displaystyle a_{i-1}</math>;
<math>\displaystyle d_i</math> = <math>\displaystyle a_i</math> - <math>\displaystyle l</math> * <math>\displaystyle c_{i-1}</math>;
<math>\displaystyle f_i</math> = <math>\displaystyle e_i</math> - <math>\displaystyle l</math> * <math>\displaystyle f_{i-1}</math>;
}
<math>\displaystyle x_1</math> = <math>\displaystyle f_N</math>;
for (i = N-1; i >= 1; i--)
<math>\displaystyle x_i</math> = <math>\displaystyle f_i</math> - <math>\displaystyle c_i</math> * <math>\displaystyle x_{i+1}</math>;
Metody bezpośrednie
Przykład: Strzałka Wilkinsona
Rozważmy układ równań z macierzą diagonalnie dominującą postaci
gdzie oznacza jakiś niezerowy element. Łatwo sprawdzić, że chociaż wyjściowa macierz jest rozrzedzona, to zastosowanie do niej eliminacji Gaussa powoduje, że w wyniku dostajemy gęste czynniki rozkładu.
Tymczasem wystarczy odwrócić kolejność równań i numerację niewiadomych (co dla macierzy jest równoznaczne z odwróceniem porządku wierszy i kolumn, korzystając z pewnej (jakiej?) macierzy permutacji ):
Wtedy okazuje się, że rozkład naszej macierzy nie powoduje już wypełnienia fill-in czynników rozkładu!
Właśnie na tym polega główny problem w rozwiązywaniu układów z macierzami rzadkimi metodami bezpośrednimi: maksymalnie wykorzystać rozrzedzenie macierzy tak, by czynniki rozkładu były możliwie mało wypełnione. Albowiem wiedząc to, będziemy mogli ograniczyć się jedynie do fizycznego wyznaczenia wartości niezerowych elementów macierzy rozkładu. Ponadto, wymagania pamięciowe algorytmu nie będą istotnie wykraczać ponad ilość pamięci potrzebnej na przechowanie danych (macierzy).
W ogólnym przypadku rozwiązanie takiego zadania jest trudne i większość algorytmów opiera się na pewnych heurystykach, które warto wspomóc wcześniejszą analizą konkretnego układu równań, który mamy rozwiązać. Najczęściej dąży się do takiego przenumerowania równań i niewiadomych, by w efekcie z góry przewidzieć, gdzie wystąpią zera w macierzach rozkładu --- i, by takich zer było jak najwięcej (by wypełnienie było jak najmniejsze)! Na architekturach z pamięcią hierarchiczną dąży się także do tego, by w trakcie rozkładu można było korzystać z BLAS3, a więc permutacje wierszy i kolumn macierzy muszą to także brać pod uwagę (tzw. metody wielofrontowe).
Stosuje się kilka strategii wyznaczania korzystnych permutacji reorderingu , z których warto wymienić
- przybliżone algorytmy minimalnego stopnia approximate minimum degree (AMD)
- techniki
podziału grafów na (prawie) rozłączne składowe (METIS).
Używają ich biblioteki takie jak UMFPACK, czy HSL.
W Octave mamy do dyspozycji także kilka procedur generujących takie permutacje,
w tym: colamd (AMD dla macierzy niesymetrycznych) oraz symamd
(AMD dla macierzy symetrycznych). Większy wybór oferuje MATLAB, jednak należy
bezwzględnie pamiętać o jednym: nie ma uniwersalnej metody reorderingu i dla
konkretnej macierzy może istnieć specjalna metoda, która da oszałamiające
rezultaty, podczas gdy standardowe podejścia nie dadzą efektu.
Przykład: Wypełnienie pewnej macierzy w zależności od użytego algorytmu
Rozważmy macierz pochodzącą z kolekcji Tima Davisa, dotyczącą pewnego zadania mechaniki strukturalnej jakie pojawiło się u Boeinga. Jest to macierz symetryczna, dodatnio określona, wymiaru 8032.

Jest to macierz silnie rozrzedzona, ponieważ ma tylko 355460 niezerowych elementów (czyli wypełnienie to tylko 0.5 procent).
Zobaczymy, jak w zależności od użytego algorytmu permutacji kolumn i wierszy poradzi sobie algorytm rozkładu Cholesky'ego.
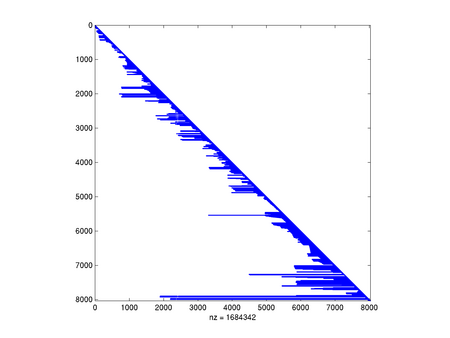
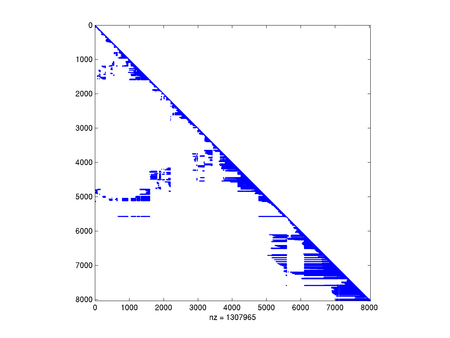
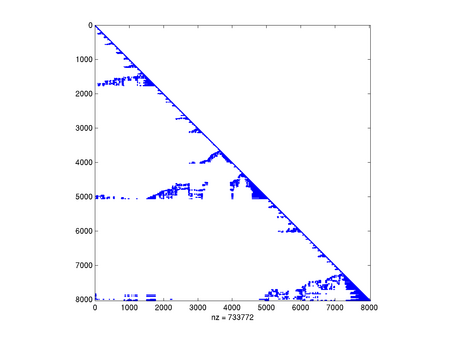
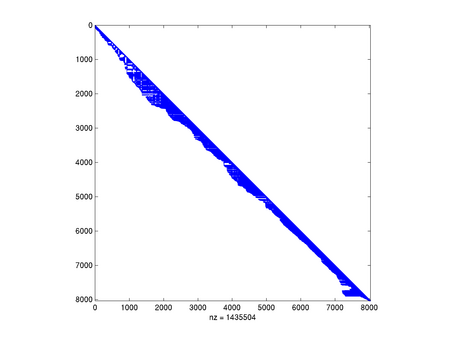
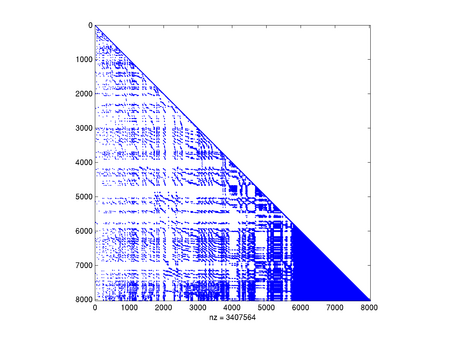
Na zakończenie popatrzmy, jak ważne jest spostrzeżenie symetrii macierzy:
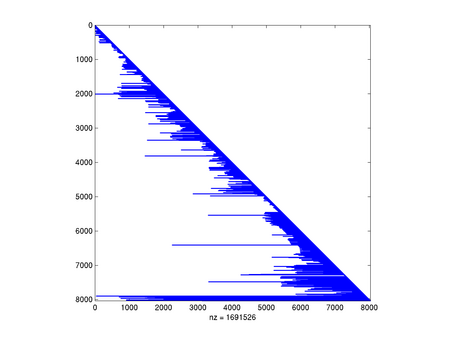
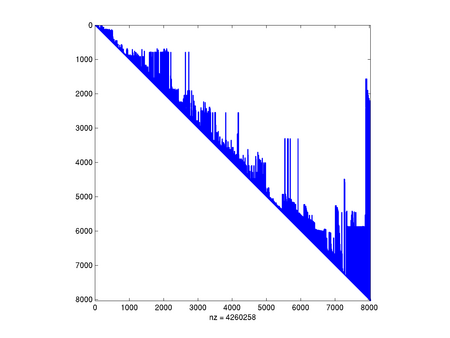
Jak widać, w naszym przypadku standardowe algorytmy (COLAMD i SYMAMD) poradziły sobie całkiem nieźle, chociaż wypełnienie i tak znacząco wzrosło. Zapewne algorytm oparty na podziale grafu na prawie rozłączne składowe mógłby tu jeszcze lepiej zadziałać.
Stacjonarne metody iteracyjne
Gdy macierz jest rozrzedzona, mnożenie takiej macierzy przez wektor jest tanie (koszt jest proporcjonalny do liczby niezerowych elementów macierzy). Dlatego, jeśli możemy zadowolić się rozwiązaniem przybliżonym układu, a w zamian osiągnąć je tanim kosztem, warto rozważyć metody iteracyjne.
Najprostsze metody iteracyjne (najprostsze w analizie i implementacji, ale --- jak można się domyślić --- w praktyce najmniej efektywne) polegają na rozkładzie macierzy na część "łatwo odwracalną", , i "resztę", . Dokładniej, jeśli jest nieosobliwa, to równanie można zapisać jako zadanie punktu stałego
gdzie . Inaczej:
i zastosować doń Dodaj link: metodę iteracji prostej Banacha:
Takie metody nazywamy stacjonarnymi metodami iteracyjnymi.
Aby przeanalizować zbieżność takiej metody, warto rozpatrzyć przypadek ogólniejszy
dla pewnej macierzy wektora (dla stacjonarnej metody iteracyjnej, oraz ).
W tym przypadku
a stąd i z nierówności , mamy
Warunkiem dostatecznym zbieżności iteracji prostych jest więc . Okazuje się, że warunkiem koniecznym i dostatecznym zbieżności tej iteracji dla dowolnego wektora startowego jest
Tak więc, metody oparte na iteracji prostej, będą zbieżne liniowo z ilorazem .
Metoda Jacobiego
Zobacz biografię
Biorąc gdzie jest macierzą diagonalną składającą się z wyrazów stojących na głównej przekątnej macierzy , układ jest równoważny układowi
a stąd (o ile na przekątnej macierzy nie mamy zera) otrzymujemy metodę iteracyjną
gdzie i , zwaną metodą Jacobiego.
W metodzie Jacobiego warunek dostateczny zbieżności, , jest spełniony np. wtedy, gdy macierz ma dominującą przekątną, tzn. gdy
Rzeczywiście, ponieważ wyraz macierzy wynosi dla oraz dla , a więc
przy czym ostatnia nierówność wynika z warunku diagonalnej dominacji.
Przykład: Macierz laplasjanu
Macierz , zwana macierzą jednowymiarowego laplasjanu
pojawia się w bardzo wielu zastosowaniach, także jako podzadanie w algorytmach numerycznych. Ta macierz jest macierzą taśmową, symetryczną i dodatnio okresloną, więc rozwiązanie układu równań z tą macierzą jest łatwe metodami bezpośrednimi, kosztem . Ciekawe będzie, jak poradzą sobie z nią metody iteracyjne.
Na przykład, w metodzie Jacobiego weźmiemy oraz . Obliczając normę macierzy iteracji Jacobiego dostajemy , co nie rozstrzyga jeszcze o jej (nie)zbieżności.
Okazuje się, że są gotowe wzory na wartości własne macierzy :
dla
i w konsekwencji, wartościami własnymi są liczby . Ponieważ , oraz to metoda, choć zbieżna, dla dużych staje się zbieżna tak wolno, że w praktyce bezużyteczna.
Zaletą stacjonarnych metod iteracyjnych jest również ich prostota, przez co są one łatwe do zaprogramowania.
Metoda Gaussa--Seidela
Ciekawostką jest, że Gauss nie miał z nią nic wspólnego, a Seidel był wręcz jej przeciwnikiem...
Złożoność stacjonarnych metod iteracyjnych
Zastanówmy się teraz nad złożonością metod iteracyjnych. Ponieważ możemy jedynie znaleźć pewne przybliżenie rozwiązania dokładnego , przez złożoność metody będziemy rozumieli koszt kombinatoryczny obliczenia z zadaną dokładnością . Dla uproszczenia założymy, że medoda jest zbieżna liniowo z ilorazem . Zauważmy, że aby zredukować błąd początkowy do , wystarczy wykonać iteracji, gdzie spełnia
czyli
Liczba ta zależy więc w istotny sposób od błędu początkowego i (przede wszystkim) od współczynnika redukcji błędu , natomiast zależność od dokładności i wymiaru układu jest dużo mniej istotna (w zadaniach praktycznych -- takich jak jednowymiarowy laplasjan --- jednak często okazuje się, że... zależy od !).
Zakładając, że koszt jednej iteracji wynosi ( jest tym mniejszy, im mniejsza jest liczba niezerowych elementów macierzy ), złożoność metody jest proporcjonalna do
Stąd oczywisty wniosek, że metody iteracyjne warto stosować zamiast metod bezpośrednich w przypadku gdy
- wymiar układu jest "duży", oraz
- macierz układu jest "rozrzedzona", tzn. ma stosunkowo niewielką liczbę elementów niezerowych, np. proporcjonalną do .
Układy o tych własnościach powstają często przy numerycznym rozwiązywaniu równań różniczkowych cząstkowych.
Metody przestrzeni Kryłowa
Zupełnie inny pomysł na realizację metody iteracyjnej przedstawiają metody przestrzeni Kryłowa, gdzie kolejne przybliżenie dobiera się w taki sposób by minimalizowało pewną miarę błędu na podprzestrzeni Kryłowa
gdzie jest residuum na początku iteracji. W zależności od wyboru sposobu miary błędu, dostajemy inną metodę iteracyjną, takie jak CG, GMRES, PCR, BiCG, i inne. Tutaj omówimy pokrótce tylko dwie najpopularniejsze: CG i GMRES.
CG
Metoda gradientów sprzężonych conjugate gradients (CG) działa przy założeniu, że jest symetryczna i dodatnio określona.
Kolejne przybliżenie ma minimalizować błąd w normie energetycznej indukowanej przez ,
na przestrzeni afinicznej . Okazuje się (co nie jest oczywiste --- trzeba skorzystać z rozmaitych własności ortogonalności generowanych wektorów), że takie zadanie minimalizacji daje się bardzo efektywnie rozwiązać, skąd dostajemy bardzo zwarty algorytm:
Algorytm
r = b-A*x;
<math>\displaystyle \rho_{-1}</math> = 0; <math>\displaystyle \rho_0</math> = <math>\displaystyle ||r||_2^2</math>; <math>\displaystyle \beta</math> = 0; k = 1;
while <math>\displaystyle \sim</math>STOP
{
p = r + <math>\displaystyle \beta</math>*p;
w = A*p;
<math>\displaystyle \alpha</math> = <math>\displaystyle \frac{\rho_{k-1}}{p^Tw}</math>;
x = x + <math>\displaystyle \alpha</math>*p;
r = r - <math>\displaystyle \alpha</math>*w;
<math>\displaystyle \rho_k</math> = <math>\displaystyle ||r||_2^2</math>;
<math>\displaystyle \beta</math> = <math>\displaystyle \frac{\rho_{k}}{\rho_{k-1}}</math>;
k++;
}
Jak widać, całą iterację da się wykonać przechowując w pamięci tylko kilka wektorów (a nie, jak możnaby się obawiać, całą przestrzeń ), a najdroższym jej elementem jest mnożenie macierzy przez wektor.
Twierdzenie Zbieżność CG jako metody bezpośredniej
Niech będzie symetryczna i dodatnio określona. Algorytm CG znajdzie dokładne rozwiązanie po co najwyżej iteracjach.
Powyższe twierdzenie, choć teoretycznie interesujące, ma małą wartość praktyczną z dwóch powodów:
- dla bardzo dużych , wykonanie iteracji może być wciąż zbyt kosztownym zadaniem
- ponieważ w arytmetyce skończonej precyzji ortogonalność z której korzysta się przy wyprowadzeniu algorytmu nie jest zachowana i w konsekwencji, po wielu iteracjach, jakość przestaje się poprawiać.
Dlatego wygodniej potraktować CG jako metodę iteracyjną. Zachodzi bowiem
Twierdzenie Zbieżność CG jako metody iteracyjnej
Po iteracjach metody CG,
gdzie .
Metoda GMRES Generalized Minimum RESidual nie wymaga ani symetrii, ani dodatniej określoności macierzy, jest więc bardziej uniwersalna, choć też bardziej kosztowna od CG.
Prekondycjoning
Zbieżność wszystkich poznanych metod iteracyjnych zależu od własności spektralnych macierzy układu. Często w zastosowaniach pojawiające się macierze mają niekorzystne własności spektralne (np. bardzo duży wskaźnik uwarunkowania) przez co metody iteracyjne zbiegają na nich bardzo wolno.
Dlatego bardzo korzystne może być wstępne przetransformowanie układu
z macierzą o niekorzystnych własnościach, do układu
gdzie macierz ma znacznie korzystniejsze własności z punktu widzenia używanej metody iteracyjnej. Taką operację nazywamy prekondycjoningiem, a macierz --- macierzą prekondycjonera.
Aby całość miała sens, macierz prekondycjonera powinna:
- być łatwa w konstrukcji,
- być tania w mnożeniu przez wektor (głównym elementem każdej metody
iteracyjnej jest mnożenie macierzy przez wektor: ),
- macierz powinna mieć znacznie korzystniejsze własności z punktu widzenia
używanej metody iteracyjnej.
Kilka ekstremalnych propozycji na macierz prekondycjonera to (łatwa w konstrukcji i tania w mnożeniu, ale nic nie polepsza, niestety...) oraz (rewelacyjnie poprawia zbieżność metody iteracyjnej, dając zbieżność w jednej iteracji, ale bardzo droga w konstrukcji i mnożeniu). Widać więc, że należy poszukiwać czegoś pośredniego, co niskim kosztem przybliża działanie macierzy odwrotnej.
Dlatego jednym z powszechniej stosowanych rodzajów prekondycjonerów są oparte na zastosowaniu jednego kroku klasycznej metody iteracyjnej.
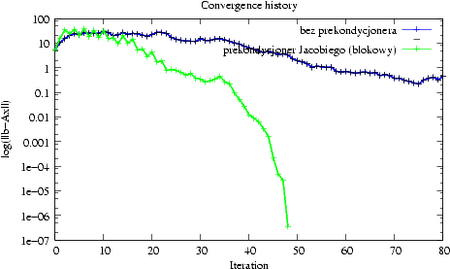
Inne prekondycjonery stosują np. techniki tzw. niepełnego rozkładu macierzy, albo --- w specyficznych przypadkach --- tzw. metody wielosiatkowe.
Okazuje się, że zarówno CG jak i GMRES da się zaimplementować tak, by w jednej iteracji było konieczne tylko jedno mnożenie przez macierz prekondycjonera.