MN03

Arytmetyka zmiennoprzecinkowa

Metody iteracyjne mają czasem kłopoty, które nie są związane z samą naturą problemu matematycznego. Przyrzyjmy się bowiem, jak w dużym zbliżeniu wygląda wykres funkcji $w(x)=x^4-4x^3+6x^2-4x+1$, której wartości zostały obliczone na komputerze PC. Nietrudno sprawdzić, że $w$ ma dokładnie jedno miejsce zerowe, gdyż $w(x)=(x-1{)}^4$. Tymczasem, wykres $w$ (wyznaczony oryginalnym wzorem) zdaje się mieć mnóstwo różnych miejsc zerowych w okolicy $x=1$. Co gorsza, wygląda na to, że $w$ wcale nie jest gładka!

Wartości funkcji $w(x)=x^4-4x^3+6x^2-4x+1$ obliczone według wzoru. Na marginesie: $w(x)=(x-1{)}^4$. Prawdziwe wartości zaznaczone na czerwono.

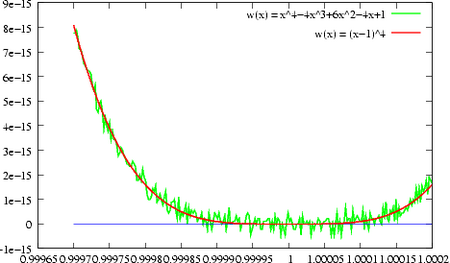
Wykonywanie realnych obliczeń na liczbach rzeczywistych w komputerze może być źródłem wielu innych zaskoczeń. Na przykład, w komputerze,

$10\cdot (1.1-1)\ne 1$

co możesz łatwo sprawdzić:

 
octave:7> 10 * (1.1 -1) - 1
ans  =     8.8818e-16

Dlatego

W praktyce numerycznej należy wystrzegać się testów w rodzaju

 
if (x  =    =    1.0) 
{
	....
}

Przedstawiony wcześniej model obliczeniowy jest modelem idealistycznym, tzn. zakłada on, że wszystkie operacje są wykonywane bezbłędnie. Dlatego w tym przypadku będziemy mówić o arytmetyce idealnej. W praktyce jednak, np. wykonując obliczenia na maszynie cyfrowej, operacje arytmetyczne na liczbach rzeczywistych wykonywane są z pewnym błędem. Matematycznym modelem arytmetyki maszyny cyfrowej jest arytmetyka $f{l}_{\nu }$ (albo arytmetyka zmiennoprzecinkowa), którą teraz przypomnimy.

Niech będzie zadana liczba naturalna $b$ (jej znaczenie wyjaśni się w następnym rozdziale). Dowolną liczbę rzeczywistą $x\ne 0$ można jednoznacznie przedstawić w postaci

$x=s\cdot 2^{c-b}\cdot m,$

gdzie $s\in \{-1,1\}$ jest znakiem, liczba całkowita $(c-b)$ cechą, a liczba rzeczywista $m\in [1,2)$ mantysą liczby $x$. Zauważmy, że taki rozkład jest jednoznaczny i odpowiada przesuwaniu przecinka w rozwinięciu binarnym liczby do pierwszej cyfry znaczącej, tj. różnej od zera (stąd nazwa: reprezentacja zmiennoprzecinkowa, ang. floating point). Mantysa ma w ogólności nieskończenie wiele cyfr binarnych $f_j$ w swoim rozwinięciu dwójkowym,

$m=1+f\equiv 1+\sum _{j=1}^{\mathrm{\infty }}{f}_j{2}^{-j}=(1.f_1{f}_2{f}_3\dots {)}_2,$

gdzie $f_j\in \{0,1\}$. Wobec tego najczęściej nie będzie mogła być zapamiętana dokładnie w pamięci komputera, gdyż możemy przechować jedynie ograniczoną liczbę cyfr cechy i mantysy.

Reprezentacja zmiennoprzecinkowa

W komputerach osobistych mamy do czynienia z reprezentacją liczb rzeczywistych, w której do zapisania liczby używa się ściśle określonej liczby bitów $t$ do zapisania mantysy i także określonej liczby bitów $p$ do zapisania cechy danej liczby niezerowej $x$:

$s{c}_1{c}_2\dots c_p{f}_1{f}_2\dots f_t$

(łącznie $1+p+t$ bitów). Liczby zapisane przy użyciu powyższej sekwencji bitów nazywa się liczbami maszynowymi. Są to jedyne dokładnie zapisywalne w komputerze liczby rzeczywiste, pozostałe będą musiały zostać wyrażone z wykorzystaniem liczb maszynowych.

Reprezentacją zmiennoprzecinkową niezerowej liczby $x$ będziemy nazywać liczbę $r{d}_{\nu }(x)$ taką, że

$r{d}_{\nu }(x)=(-1{)}^s\cdot (1+f)\cdot 2^{c-b},$

gdzie $f$ jest liczbą dwójkową postaci $(0.f_1\dots f_t{)}_2$, natomiast $c$ jest liczbą naturalną postaci $(c_1\dots c_p{)}_2$. Na znak liczby, $s$, przeznaczony jest jeden bit. Wartości $c$ i $f$ dobiera się tak, żeby $r{d}_{\nu }(x)$ była tak bliska $x$ jak to możliwe. Stałą całkowitą $b$ dobiera się tak, by uzyskać zbalansowany zakres cechy $c-b$ (mniej więcej tyle samo wartości ujemnych i dodatnich), a zysk z korzystania z niej jest taki, że nie marnujemy dodatkowego bitu na przechowywanie znaku wykładnika potęgi dwójki $c-b$.

Przy takim sposobie reprezentacji, jej błąd względny szacuje się przez

$\left|\frac{r{d}_{\nu }(x)-x}{x}\right|\le \frac{1}{2^{t+1}}.$

Liczbę $\nu =\frac{1}{2^{t+1}}$ nazywa się precyzją arytmetyki. Jak widać, ma ma ona wpływ na to, jak wiele cyfr znaczących liczby jest reprezentowanych dokładnie. Precyzja arytmetyki zależy wyłącznie od liczby bitów przeznaczonych na reprezentację mantysy.

Ostatnią nierówność wygodnie jest zapisać w równoważny sposób jako

$r{d}_{\nu }(x)=x(1+ϵ),\text{gdzie}|ϵ|\le \nu .$

Przykład

Rozważmy bardzo prościutki system, w którym zarówno na cechę, jak i mantysę, przeznaczone są jedynie po dwa bity, zatem jedna liczba maszynowa zajmuje 5 bitów. Ponieważ w konsekwencji możliwy zakres wartości $c$ to $0,\dots ,3$, rozsądne jest więc przyjęcie korekty $b=1$, dzięki czemu $-1\le c-b\le 2$. Z kolei możliwe wartości mantysy to

$(1.00{)}_2=1,(1.01{)}_2=1.25,(1.10{)}_2=1.5,(1.11{)}_2=1.75.$

Wobec tego, jedyne (dodatnie) liczby maszynowe naszej pięciobitowej arytmetyki zmiennopozycyjnej to

$0.500,0.625,0.750,0.8751.000,1.250,1.500,1.7502.000,2.500,3.000,3.5004.000,5.000,6.000,7.000$

Liczby maszynowe: reprezentowane dokładnie w pięciobitowej arytmetyce o precyzji $2^{-2}$. (Przedstawiliśmy tylko liczby nieujemne)

Standard IEEE 754

Plik:Kahan.jpg

William Kahan
Guru arytmetyki zmiennoprzecinkowej i współtwórca [http://www.cs.berkeley.edu/ wkahan/ieee754status/754story.html standardu IEEE754] Zobacz biografię

Z nielicznymi egzotycznymi wyjątkami (np. Cray C90), współczesne procesory używane w komputerach osobistych lub większych, implementują IEEE 754 Floating Point Standard, który definiuje dwa zasadnicze formaty reprezentacji zmiennoprzecinkowej liczb rzeczywistych:

Typ IEEE 754	Pojedycznej precyzji	Podwójnej precyzji
Nazwa typu w C	float	double
Liczba bitów cechy	8	11
Liczba bitów mantysy	23	52
Liczba bajtów dla typu w C	4	8
Bias (liczba $b$ powyżej)	127	1023
Orientacyjny zakres	$10^{-38}\dots 10^{+38}$	$10^{-308}\dots 10^{+308}$
Orientacyjna precyzja	$6\cdot 10^{-8}$	$10^{-16}$

(maksymalna i minimalna wartość cechy $c$ ma specjalne znaczenie). Dodatkowo, w procesorach x86 mamy typ podwójnej rozszerzonej precyzji (także zdefiniowany w IEEE 754 i odpowiadający dokładnie ówczesnym możliwościom procesora Intel 8087; procesory Intela mają zresztą jedną z najlepszych implementacji IEEE 754). Wszystkie operacje arytmetyczne na procesorach x86 są faktycznie wykonywane w takiej precyzji (korzystając z 64 bitów dla reprezentacji mantysy i 15 bitów dla cechy). Należy pamiętać, że odpowiadający mu typ w C long double zajmuje w pamięci 12 bajtów (a nie 80 bitów).

Uwaga

Producenci niektórych procesorów świadomie rezygnują z pełnej implementacji IEEE 754 dla zwiększenia szybkości działania, niestety czasem kosztem dokładności wyniku. Tak dawno temu było w procesorach Cray; tak też działają niektóre instrukcje wektorowe (z tzw. zestawu 3DNow!) w procesorach AMD, które np. wynik dzielenia wektorowego zwracają z precyzją tylko 14 bitów mantysy. Procesor IBM Cell (stosowany w Sony Playstation 3) również także [http://domino.watson.ibm.com/comm/research.nsf/pages/r.arch.innovation.html nie

w pełni implementuje IEEE 754].

W Octave można łatwo podejrzeć reprezentację binarną liczby zmiennoprzecinkowej podwójnej precyzji (jest to domyślny typ numeryczny stosowany w MATLABie i Octave),

 
octave:9> format bit
octave:10> x  =    -2
x  =    1100000000000000000000000000000000000000000000000000000000000000
octave:11> x  =    1/4
x  =    0011111111010000000000000000000000000000000000000000000000000000
octave:12> x  =    NaN
x  =    1111111111111000000000000000000000000000000000000000000000000000
octave:13> x  =    0
x  =    0000000000000000000000000000000000000000000000000000000000000000
octave:14> x  =    Inf
x  =    0111111111110000000000000000000000000000000000000000000000000000
octave:15> x  =    0.1
x  =    0011111110111001100110011001100110011001100110011001100110011010

(w MATLABie możemy zobaczyć tę samą liczbę w zapisie szestnastkowym).

Przykład: Nawet liczba 0.1 nie jest reprezentowana dokładnie!

Rozwinięcie dwójkowe liczby 0.1 jest nieskończone:

$0.1=(0.0001100110011001\dots {)}_2.$

Ten banalny fakt jest bardzo często przeoczany przez programistów, a w 1991 roku doprowadził nawet do spektakularnej awarii systemu antyrakietowego Patriot. Okazało się, że --- w tajemniczy sposób --- zazwyczaj bezbłędnie trafiające w cel rakiety Patriot traciły skuteczność, gdy przez wiele godzin pozostawały w stanie gotowości.

Plik:Patriot missile launch.jpg

System rakietowy Patriot

Wyjaśnienie zagadki leżało na styku pomiędzy hardware a software rakiety. Jak zbadano, w celu pomiaru czasu, zliczano kolejne tyknięcia zegara rakiety, które następowały dokładnie co 0.1 sekundy. Następnie, w celu wyznaczenia prawdziwego czasu, mnożono liczbę tyknięć zegara przez 0.1 (które właśnie było niedokładnie reprezentowane). Gdy cykli zegara było bardzo dużo, błąd bezwzględny wyznaczenia czasu stawał się na tyle poważny, że uniemożliwiał precyzyjne wyznaczenie parametrów toru lotu nieprzyjacielskiego obiektu!

Na marginesie zauważmy, że np. liczba $0.125$ jest reprezentowana dokładnie w arytmetyce zmiennoprzecinkowej (dlaczego?) i nie powodowałaby już tego problemu. Podobnie dawałoby się uniknąć problemu, działając wyłącznie na różnicach liczby tyknięć...

Więcej informacji o najróżniejszych katastrofach spowodowanych błędami w programowaniu można przeczytać na stronach Thomasa Huckle.

Uwaga

Nie wszystkie maszyny liczące wykorzystują reprezentację dwójkową. Kiedyś zdarzały się komputery reprezentujące liczby w postaci

$x=s\cdot {\beta }^c\cdot m,$

gdzie $\beta =8$ lub 16, a nawet 3 (sic!). Do dzisiaj, w podręcznych kalkulatorach najczęściej spotykaną podstawą reprezentacji liczb jest $\beta =10$.

Są także takie realizacje arytmetyki zmiennoprzecinkowej, które nie realizują w pełni standardu IEEE (np. stare komputery Cray) i np. zamiast zaokrąglenia, stosują obcięcie wyniku.

Standard IEEE 754 jest obecnie uaktualniany, jego nowa wersja powinna ukazać się pod koniec 2006 roku.

Nadmiar i niedomiar

W maszynie cyfrowej cecha $c$ liczby rzeczywistej nie może oczywiście mieć dowolnie dużej wartości bezwzględnej, $|c|\le c_{\max }$, dlatego nie wszystkie liczby rzeczywiste są w ogóle reprezentowalne. Powoduje to powstanie zjawiska nadmiaru gdy dla liczby $xc>c_{\max }$, oraz zjawiska niedomiaru gdy $c<-c_{\min }$. W pierwszym przypadku liczba jest tak duża (co do modułu), że nie zawiera się w przedziale liczb reprezentowalnych, a w drugim jest tak mała, że musi być reprentowana przez zero, przy czym błąd względny reprezentacji wynosi wtedy $1$ a nie $\nu$.

Próżnia wokół zera (na przykładzie 5-bitowej arytmetyki)

Arytmetyka IEEE 754 przyjmuje, że liczby dla których następuje overflow są reprezentowane przez specjalną wartość Inf (nieskończoność, ze znakiem), która propaguje się w obliczeniach zgodnie z powszechnie przyjętymi regułami, np. 1+Inf daje Inf, 1/Inf daje 0, Inf-Inf daje NaN, itd.

Wszystkie liczby większe od największej zapisywalnej liczby są reprezentowane przez Inf (na przykładzie 5-bitowej arytmetyki)

W dalszych rozważaniach zjawiska nadmiaru i niedomiaru będziemy dla uproszczenia zaniedbywać, jednak nie zawsze jest to uzasadnione, o czym niech świadczy poniższy przykład.

Przykład: Wyznaczanie normy euklidesowej wektora

Jedną z najczęściej wykonywanych operacji na wektorze $x=(x_1,\dots ,x_n{)}^T\in R^n$ jest obliczenie jego normy euklidesowej,

$||x|{|}_2=\sqrt{x_1^2+\dots x_n^2}.$

Jak widać, możemy tu łatwo zetknąć się ze zjawiskiem zarówno niedomiaru, jak i nadmiaru, gdyż może się na przykład tak złożyć, że mimo iż $||x|{|}_2$ jest reprezentowana, to $x_1^2$ już nie (np. w arytmetyce podwójnej precyzji $x_1=10^{200}$ i $x_2=1$).

Łatwym wyjściem z tej sytuacji jest wstępna normalizacja danych tak, by wszystkie nie były większe od 1: niech $M=\max \{|x_i|:i=1,\dots ,n\}$ i wtedy

$||x|{|}_2=\sqrt{x_1^2+\dots x_n^2}=M\cdot \sqrt{{\left(\frac{x_1}{M}\right)}^2+\dots +{\left(\frac{x_1}{M}\right)}^2}.$

i teraz suma pod pierwiastkiem jest zawsze pomiędzy 1 a $N$. Wadą omówionego rozwiązania jest to, że wymaga ono dwukrotnego przejrzenia całego wektora (raz, by znaleźć $M$, drugi raz --- by policzyć sumę. Na szczęście można go zmodyfikować tak, by działał w jednym przebiegu. Zupełnie inny algorytm podał Moler.

Liczby denormalizowane

Wymaganie, że mantysa jest postaci $1+f$, $f\ge 0$, powoduje, że wokół zera pojawia się coś w rodzaju próżni. Formalnie, liczby mniejsze niż $2^{1-1023}$ powinny być reprezentowane przez 0, lecz zazwyczaj zamiast tego

 
octave:16> format bit
octave:17> x  =    2^(-1022)
x  =    0000000000010000000000000000000000000000000000000000000000000000
octave:18> x  =    2^(-1023)
x  =    0000000000001000000000000000000000000000000000000000000000000000
octave:19> x  =    2^(-1028)
x  =    0000000000000000010000000000000000000000000000000000000000000000

W ten sposób można (w podwójnej precyzji) zbliżyć się do zera na odległość około $10^{-323}$.

Liczby denormalizowane trochę wypełniają próżnię wokół zera

Działania arytmetyczne w arytmetyce $f{l}_{\nu }$

W arytmetyce $f{l}_{\nu }$ implementującej standard IEEE 754, działania arytmetyczne na liczbach rzeczywistych (a raczej na ich reprezentacjach) są wykonywane dokładnie i tylko wynik jest zaokrąglany. Mamy więc

$f{l}_{\nu }(x◻y)=r{d}_{\nu }(r{d}_{\nu }(x)◻r{d}_{\nu }(y)),$

gdzie $◻\in \{+,-,\times ,÷\}$, Ogólniej, jeśli ${{𝒲}}_1$ i ${{𝒲}}_2$ są wyrażeniami o wartościach rzeczywistych, to dla dowolnych wartości zmiennych

$f{l}_{\nu }({{𝒲}}_1◻{{𝒲}}_2)=r{d}_{\nu }(f{l}_{\nu }({{𝒲}}_1)◻f{l}_{\nu }({{𝒲}}_2)).$

Zwykle dla prostoty będziemy również zakładać podobną zależność dla niektórych funkcji standardowych, o ile należą one do zbioru operacji elementarnych (chociaż w rzeczywistości są one obliczane przez procedury używające czterech podstawowych operacji arytmetycznych). I tak będziemy mieć np.

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned fl_\nu\Big(\sqrt{{\cal W}}\Big) &= \left(\sqrt{fl_\nu({\cal W})}\right) (1+\beta_1),\\ fl_\nu(\cos({\cal W})) &= \left(\cos(fl_\nu({\cal W}))\right)(1+\beta_2), \endaligned}

gdzie $|{ϵ}_j|\le \nu$, oraz ${\beta }_j\le K_j\nu$ i $K_j$ są "niewielkimi" stąłymi.

Przypuśćmy, że w naszym prościutkim pięciobitowym systemie spełniającym wymogi standardu IEEE 754 zechcemy wykonać mnożenie

$1.3\cdot 2.4$

Poniżej możemy przekonać się, jak będzie ono przebiegać (na przykładzie 5-bitowej arytmetyki).

<flash>file=binarysystem4.swf</flash><div.thumbcaption>Mnożenie dwóch liczb rzeczywistych (na przykładzie 5-bitowej arytmetyki)

Podobnie, jeśli $\mathrm{△}$ jest operatorem porównania, $\mathrm{△}\in \{<,\le ,=,\ne \}$, to wartością wyrażenia logicznego ${{𝒲}}_1\mathrm{△}{{𝒲}}_2$ w $f{l}_{\nu }$ jest dokładna wartość wyrażenia Parser nie mógł rozpoznać (nieznana funkcja „\trianglefl”): {\displaystyle \displaystyle fl_\nu({\cal W}_1)\trianglefl_\nu({\cal W}_2)} .

Dosyć dziwnie w porównaniach zachowuje się specjalna liczba NaN (ang. not-a-number), dla której zawsze zachodzi, że NaN$\ne$NaN. Liczba NaN pojawia się jako wynik zabronionych operacji matematycznych, np. $0/0,\sqrt{-2},$ Inf - Inf, itp., i także propaguje się w dalszych obliczeniach.

Działania arytmetyczne nie są łączne, co widać na poniższym przykładzie:

 
octave:9> 7.1 - (7+0.1)
ans  =    0
octave:10> (7.1 - 7) - 0.1
ans  =     -3.6082e-16

Wbrew pozorom, fakt, że nie mamy dostępu do arytmetyki nieskończonej precyzji może mieć daleko idące konsekwencje, o czym przekonaliśmy się na początku wykładu.

Praktyczne wyznaczanie precyzji arytmetyki

Aby wyznaczyć precyzję używanej przez nas arytmetyki możemy wykonać prosty test. Pomyślmy, jaka jest najmniejsza dodatnia liczba ${ϵ}_{\text{mach}}$, która dodana do jedności da w wyniku liczbę większą od 1.0 (liczbę ${ϵ}_{\text{mach}}$ nazywa się czasem epsilonem maszynowym, macheps). Jasne jest, że w przypadku arytmetyki IEEE 754 jest to liczba równa podwojonej precyzji arytmetyki, $2^{-t}$, gdzie $t$ jest liczbą cyfr mantysy $f$. Stąd dostajemy prosty algorytm wyznaczania epsilona maszynowego:

 
x  =    1.0;
while ( 1.0 + x > 1.0 )
{
	x  =    x / 2.0;
}
printf("Macheps  =    %g", 2.0*x);
}

Jednak, w rzeczywistości musimy być bardziej ostrożni. Implementując ten algorytm w C następująco

 
/* Wyznaczanie epsilona maszynowego, wersja 1 */
#include <stdio.h>

int main(void)
{
	int dt;
	double dx;

	dt  =    0; dx  =    1.0;
	while(1.0 + dx > 1.0) 
	{
		dx * =    0.5;
		dt++;
	}
	printf("Macheps (double)  =    %g. Liczba bitów mantysy  =    %d\n", 2*dx, dt);
	return(0);
}	

dostajemy wynik niezgodny z oczekiwaniami:

 
Macheps  =    1.0842e-19. Liczba bitów mantysy  =    64.

Wynika to stąd, że w C obliczenia wykonują się zawsze z maksymalną możliwą precyzją. W procesorach x86 jest to precyzja arytmetyki extended double precision, wykorzystującej 80 bitów do reprezentacji liczb. Dlatego działanie

 
1.0 + dx > 1.0

wykona się w arytmetyce nie podwójnej (64-bitowej), ale rozszerzonej podwójnej precyzji, 80-bitowej. Aby sprawić, by działanie zostało wykonane z wykorzystaniem typu double, musimy nasz program trochę zmodyfikować:

 
/* Wyznaczanie epsilona maszynowego, wersja 2 */
#include <stdio.h>

int main(void)
{
	int dt;
	double dx, dxp1;
	
	dt  =    0; dx  =    1.0; dxp1  =    2.0;
	while(dxp1 > 1.0) 
	{
		dx * =    0.5;
		dxp1  =    1.0 + dx; /* tym razem wynik działania zostanie zapisany
				do zmiennej typu double */
		dt++;
	}
	printf("Macheps (double)  =    %g. Liczba bitów mantysy  =    %d\n", 2*dx, dt);
}

Tym razem wynik jest prawidłowy:

 
Macheps  =    2.22045e-16. Liczba bitów mantysy  =    53

Ćwiczenie

Sprawdź, jak zmienią się wyniki, gdy wykorzystasz w swoim programie (zarówno w wersji 1, jak w wersji 2) opcje kompilacji:

• gcc -O3
• gcc -ffast-math
• gcc -O3 -ffast-math

Spróbuj objaśnić te wyniki, wspomagając się ewentualnie dokumentacją kompilatora.

Dodaj link: LAPACK daje gotową funkcję, DLAMCH (dla liczb podwójnej precyzji) i SLAMCH (dla pojedynczej precyzji), pozwalającą stwierdzić eksperymentalnie, jakie są parametry używanej arytmetyki, m.in. zakres liczb reprezentowalnych, w jakim systemie reprezentowana jest mantysa, oraz oczywiście precyzję arytmetyki i liczbę cyfr mantysy. Polecamy analizę kodu źródłowego LAPACK/dlamch1.f oraz lekturę prac

• Malcolm M. A. (1972) Algorithms to reveal properties of floating-point arithmetic. Comms. of the ACM, 15, 949-951.
• Gentleman W. M. and Marovich S. B. (1974) More on algorithms that reveal properties of floating point arithmetic units.

Comms. of the ACM, 17, 276-277.

na których oparto tę funkcję LAPACKa. Poniżej przykład zastosowania tej funkcji i wyniki uzyskane na procesorze x86.

 
/* Wyznaczanie epsilona maszynowego i innych charakterystyk arytmetyki podwójnej
precyzji z wykorzystaniem funkcji DLAMCH z LAPACKa */
#include <stdio.h>
#include <math.h>

double dlamch_(char *CMACH); /* funkcja DLAMCH z LAPACKa */

int main(void)
{
char CMACH;

	CMACH  =    'e';
	printf("Epsilon maszynowy: %g\n", dlamch_(&CMACH));
	CMACH  =    'b';
	printf("Podstawa arytmetyki: %g\n", dlamch_(&CMACH));
	CMACH  =    'n';
	printf("Liczba bitów mantysy: %g\n", dlamch_(&CMACH));
	CMACH  =    'u';
	printf("Zakres: %g ", dlamch_(&CMACH));
	CMACH  =    'o';
	printf("... %g\n", dlamch_(&CMACH));
	CMACH  =    'r';
	return(0);
}

 
Epsilon maszynowy: 2.22045e-16
Podstawa arytmetyki: 2
Liczba bitów mantysy: 53
Zakres: 2.22507e-308 ... 1.79769e+308

==Wpływ błędu zaokrągleń na wyniki obliczeń. Redukcja cyfr i inne patologie==

Korzystając z wprowadzonego powyżej modelu arytmetyki zmiennoprzecinkowej możemy spróbować uchwycić wpływ błędu reprezentacji i błędu zaokrągleń na wynik konkretnego algorytmu.

Przykład

Rozważmy banalne zadanie wyznaczenia iloczynu $N$ liczb z tablicy $x$,

$s=x_0\cdot \cdots \cdot x_{N-1}.$

W tym celu stosujemy banalny algorytm:

 
s  =    1.0;
for (i =   0; i < N; i++)
	s * =    x[i];

Sprawdźmy, jak będzie on realizowany w arytmetyce zmiennoprzecinkowej. Dla uproszczenia założymy, że nie wystąpiło ani zjawisko nadmiaru, ani zjawisko niedomiaru (w przeciwnym razie dostaniemy w wyniku, odpowiednio, $\pm$Inf lub 0).

Naturalnie, zamiast dokładnych wartości $x_0,\dots x_{N-1}$, będziemy mieli w komputerze jedynie ich reprezentacje, ${\tilde{x}}_i=r{d}_{\nu }(x_i)=x_i(1+{\delta }_i)$, przy czym $|{\delta }_i|\le \nu$.

Oznaczając ${\tilde{s}}_i$ wyznaczoną numerycznie wartość iloczynu po $i$-tym kroku pętli, mamy, że

${\tilde{s}}_{i+1}=f{l}_{\nu }({\tilde{s}}_i\times {\tilde{x}}_i)={\tilde{s}}_i\cdot {\tilde{x}}_i\cdot (1+{ϵ}_i),$

gdzie znów $|{ϵ}_i|\le \nu$. Ostatecznie więc, wyznaczona wartość iloczynu, $\tilde{s}$ spełnia

$\tilde{s}=x_0\cdots x_{N-1}\cdot {\mathrm{\Pi }}_{i=0}^{N-1}(1+{ϵ}_i)(1+{\delta }_i).$

Ponieważ ${\mathrm{\Pi }}_{i=0}^{N-1}(1+{ϵ}_i)=(1+{ℰ})$, gdzie, z pominięciem małych wyższego rzędu, $|{ℰ}|\le N\nu$, dostajemy ostatecznie

$\tilde{s}=s\cdot (1+E),$

gdzie $|E|\le 2N\nu$. Ponieważ w arytmetyce podwójnej precyzji $\nu \approx 10^{-16}$, to nawet biorąc iloczyn tysiąca (!) liczb, dostajemy wynik, którego błąd względny będzie (o ile tylko nie wystąpi nadmiar/niedomiar) bardzo mały, rzędu $10^{-13}$!

Powyższe rozumowanie, a także intuicja często wyrażana przez osoby postronne, prowadzi do przypuszczenia, że:

\beginbadquote "Duży błąd względny wyniku jest możliwy dopiero po kumulacji błędów zaokrągleń po przeprowadzeniu bardzo wielu działań arytmetycznych." \endbadquote

Jednak to jest to całkowicie fałszywy pogląd, o czym świadczy kolejny, bardzo znamienny przykład.

Przykład: Redukcja cyfr przy odejmowaniu

Tym razem nasze zadanie jest znacznie prostsze od poprzedniego. Trzeba wyznaczyć po prostu różnicę dwóch liczb:

$s=a-b.$

Prowadząc analizę jak poprzednio, widzimy, że obliczona numerycznie wartość to

$\tilde{s}=f{l}_{\nu }(r{d}_{\nu }(a)-r{d}_{\nu }b)=(a(1+{\delta }_a)-b(1+{\delta }_b))(1+ϵ),$

Stąd po prostych oszacowaniach

$\left|\frac{\tilde{s}-s}{s}\right|\le 2\frac{|a|+|b|}{|a-b|}\cdot \nu .$

A więc, gdy $a\approx b$, to $\frac{|a|+|b|}{|a-b|}\approx \mathrm{\infty }$ i w efekcie możemy utracić nawet wszystkie znaczące cyfry wyniku! To zjawisko właśnie nosi żargonową nazwę utraty cyfr przy odejmowaniu, choć precyzyjnie powinno się mówić o "zmniejszeniu liczby dokładnych cyfr znaczących wyniku przy odejmowaniu dwóch bardzo bliskich sobie liczb".

Przy okazji zauważmy, że prowadząc identyczną analizę dla sumy dwóch liczb $a+b$, gdzie $a$ i $b$ są tego samego znaku, dostajemy oszacowanie błędu względnego równe $2\nu$, niezależnie od wartości liczbowych $a$ i $b$!

Skutki zjawiska redukcji cyfr przy odejmowaniu mogą być dramatyczne i ujawnić się w nadspodziewanie elementarnych sytuacjach.

Numeryczne kłopoty z wyznaczaniem pierwiastków trójmianu kwadratowego

Niech $a,p,q>0$. Korzystając ze szkolenego wzoru na pierwiastki równania kwadratowego $a{x}^2-2px+q=0$

$x_{1,2}=\frac{1}{a}(p\pm \sqrt{\mathrm{\Delta }}),$

gdzie $\mathrm{\Delta }=p^2-qa>0$, możemy natknąć się na trudności, gdy jeden z pierwiastków jest bardzo bliski zera (tzn. gdy $p\approx \sqrt{\mathrm{\Delta }}$).

Taka sytuacja np. powstaje gdy rozważać jednostajnie opóźniony ruch pocisku wystrzelonego z działka przeciwlotniczego do celu lecącego na małej wysokości. Czas trafienia w cel jest --- przy pominięciu oporu powietrza --- rozwiązaniem równania kwadratowego, przy czym czs krótki odpowiada bezpośredniemu trafieniu w cel, a czas długi --- wystrzeleniu pocisku z wyprzedzeniem wysoko w górę i poczekaniu, aż spadając trafi w cel od góry. Oczywiście, żaden artylerzysta nie będzie się interesował tym ostatnim przypadkiem: interesujące jest więc dokładne (bo cel leci szybko) wyznaczenie mniejszego pierwiastka.

Niestety, skoro $p\approx \sqrt{\mathrm{\Delta }}$, to wyznaczając mniejszy pierwiastek $x_1$ ryzykujemy utratę cyfr przy odejmowaniu. Ale na szczęście, można to ominąć zgodnie z często stosowaną w numeryce regułą:

Jeśli problem jest trudny --- najlepiej zmienić problem!

W naszym wypadku ratunkiem jest matematyczna transformacja problemu tak, by już nie było w nim odejmowania bliskich sobie liczb. Rzeczywiście, przecież wciąż mamy dobry wzór na większy z pierwiastków, $x_2=\frac{1}{a}(p+\sqrt{\mathrm{\Delta }})$! Dokładając do tego wzór Viete'a,

$x_1{x}_2=\frac{q}{a},$

dostajemy inny wzór na $x_1$, nie zawierający feralnego odejmowania. Poniżej demonstrujemy program w C, testujący jakość obu podejść.

# include <stdio.h>
# include <math.h>

/* w(x)  =    ax^2 - 2px + q  =    0  */
/* delta  =    4(p^2 - qa) */

double const a  =    2.1, q  =    1e-6, p =   1.1;

double w(double x) /* wartość wielomianu w punkcie x */
{
	return(a*x*x - 2.0*p*x + q);
}

int main(void)
{
	double x1, x2, x1v, X1, X1v, X2;
	double Delta; /* wartość Delty liczymy w podwójnej   precyzji */
	float  delta; /* wartość delty liczymy w pojedynczej precyzji */
		
	delta  =    Delta  =    sqrt(p*p - q*a);
	printf("Wielomian w(x)  =    %e x^2 - %e x + %e.\nDelta  =    %e\n", a, 2*p, q, delta);

	/* pierwiastki liczone wzorem szkolnym, z niedokładną deltą */
	x1  =    (p - delta)/a;
	x2  =    (p + delta)/a;
	
	/* mniejszy pierwiatek, liczony z mało dokładną deltą, ale lepszym
	wzorem: Viete'a */
	x1v  =    (q/a)/x2;
	
	/* pierwiastki liczone wzorem szkolnym, z dokładniejszą Deltą */
	X1  =    (p - Delta)/a;
	X2  =    (p + Delta)/a;
	
	/* mniejszy pierwiatek, liczony z dokładniejszą Deltą, ale lepszym
	wzorem: Viete'a */
	X1v  =    (q/a)/X2;

	printf("\nPierwiastki z mało dokładną deltą:\n");
	printf(" Wzór szkolny: x1   =    %e x2  =    %e\n Wzór Viete'a: x1v  =    %e x2  =    j.w.\n", 
	x1,x2,x1v);
	printf("\nPierwiastki z dokładniejszą Deltą:\n");
	printf(" Wzór szkolny: X1   =    %e X2  =    %e\n Wzór Viete'a: X1v  =    %e X2  =    j.w.\n", 
	X1,X2,X1v);
	printf("\nWzględna zmiana wartości pierwiastka:\n");
	printf("   (x1 - x1v)/x1v  =    %e\n", (x1-x1v)/x1v);
	printf("   (x1v -X1v)/X1v  =    %e\n", (x1v-X1v)/X1v);
	printf("   (x2 -  X2)/X2   =    %e\n", (x2-X2)/X2);
	
	printf("\nWartość wielomianu w wyznaczonych punktach:\n");
	printf(" w(x1)   =    %e\n w(x1v)  =    %e w(X1v)  =    %e\n w(x2)   =    %e\n w(X2)  =    %e\n ", 
		w(x1),w(x1v),w(X1v),w(x2),w(X2));
	
	return(0);
}

 
Wielomian w(x)  =    2.100000e+00 x^2 - 2.200000e+00 x + 1.000000e-06.
Delta  =    1.099999e+00

Pierwiastki z mało dokładną deltą:
 Wzór szkolny: x1   =    4.427774e-07 x2  =    1.047619e+00
 Wzór Viete'a: x1v  =    4.545456e-07 x2  =    j.w.

Pierwiastki z dokładniejszą Deltą:
 Wzór szkolny: X1   =    4.545457e-07 X2  =    1.047619e+00
 Wzór Viete'a: X1v  =    4.545457e-07 X2  =    j.w.

Względna zmiana wartości pierwiastka:
   (x1 - x1v) / x1v  =    -2.589022e-02
   (x1v -X1v) / X1v  =    -1.123337e-08
   (x2 -  X2) / X2   =    1.123337e-08

Wartość wielomianu w wyznaczonych punktach:
 w(x1)   =    2.589022e-08
 w(x1v)  =    1.123337e-14, w(X1v)  =    -3.194985e-23
 w(x2)   =    2.589022e-08
 w(X2)  =    -1.357688e-17

Jak więc widzimy, nawet z niezbyt dokładnie wyznaczoną deltą, mniejszy pierwiastek jesteśmy w stanie wyznaczyć bardzo precyzyjnie --- o ile tylko unikniemy redukcji cyfr przy odejmowaniu.

Przykład: Powiększenie?

Ten obrazek już widzieliśmy na początku wykładu.

Wykres funkcji $w(x)=x^4-4x^3+6x^2-4x+1=(x-1{)}^4$ wyznaczony (w bardzo bliskiej okolicy zera) na dwa sposoby w arytmetyce podwójnej precyzji.

Wyjaśnieniem tej niepokojącej obserwacji jest znowu zjawisko redukcji cyfr przy odejmowaniu: wartości $f$ są bliskie zera, a powstają jako suma dużych liczb z przeciwnymi znakami.

Czasem możemy spotkać się z twierdzeniem, że nie warto zawracać sobie głowy metodami numerycznymi, gdyż są dostępne pakiety obliczeń symbolicznych (Maple, Mathematica, MuPAD, Maxima), które potrafią "wszystko policzyć z dowolną precyzją".

To oczywiście też nie jest do końca prawdą. Precyzja, o której mowa, jest jedynie precyzją używanej arytmetyki (rzeczywiście, softwarowo można emulować dowolną precyzję), ale dokładność wyniku nie może być w nich a priori zadana. Wiele bowiem może zależeć od właściwości samego zadania obliczeniowego, o czym mówimy w następnej części wykładu. Na razie prosty przykład:

Przykład: Co oznacza precyzja w pakietach symbolicznych

Oto fragment sesji pakietu obliczeń symbolicznych MUPAD:

 
>> ((4/3)*3 - 3) - 1

                                     0
>> DIGITS : =    10

                                    10
>> ((4/3.0)*3 - 3) - 1

                             -2.168404345e-19
>> subs(((4/a)*3 - 3) - 1, a  =    3.0)

                              -4.33680869e-19
>> subs(((4/a)*3 - 3) - 1, a  =    3)

                                     0

Najpierw wyznaczona została wartość wyrażenia algebraicznego, korzystając z manipulacji symbolicznej --- oczywiście bez trudu system stwierdził, że to wyrażenie upraszcza się do zera.

Następnie zażądaliśmy, by DIGITS --- parametr sterujący "liczbą cyfr znaczących dla liczb zmiennoprzecinkowych", jak to określa manual MUPADa --- przyjął wartość równą 10.

Wymuszając, przez podanie 3.0 zamiast 3 stosowanie w obliczeniach arytmetyki zmiennoprzecinkowej zamiast symbolicznej (pamiętasz, jak to jest w C?) dostajemy wynik, który nie ma ani jednej cyfry znaczącej dokładnej. Z drugiej strony, widzimy także, iż faktycznie stosowana precyzja obliczeń jest znacznie większa i wynosi około 19 cyfr znaczących, chociaż żądaliśmy jedynie 10...

Jak wynika z powyższego, w praktyce pakiety symboliczne stosują znacznie większą niż żądana precyzję obliczeń, by ustrzec się najbardziej typowych patologii. I faktycznie, zazwyczaj taka strategia (choć kosztowna) jest satysfakcjonująca!

Własności zadania obliczeniowego i algorytmu numerycznego

Uwarunkowanie zadania obliczeniowego

Jak zobaczyliśmy w poprzednich przykładach, dane, jakimi dysponujemy wykonując zadanie obliczeniowe są z natury rzeczy wartościami zaburzonymi. Źródłem tych zaburzeń są:

• błąd reprezentacji danych w arytmetyce zmiennoprzecinkowej (0.1 nie jest

równe dokładnie $1/10$)

• błędy w parametrach będących rezultatem poprzednich obliczeń (chcemy

rozwiązać równanie $f(x)=a$, ale $a$ jest rezultatem innej symulacji), a także

• błędy pomiarowe w zadaniach praktycznych (chcemy policzyć

numeryczną prognozę pogody, ale temperaturę wyjściową znamy tylko z dokładnością do 0.1 stopnia, co gorsza --- z niektórych stacji w ogóle nie mamy danych)

Okazuje się, że powszechna intuicja, że małe zaburzenia danych powinny dawać małe zaburzenia wyniku, nie znajduje potwierdzenia nawet w bardzo prostych przypadkach. Z drugiej strony, umiejętność oceny jakościowego wpływu zaburzenia danych na wynik jest kapitalna w świecie obliczeń numerycznych w ogólności, a w szególności --- inżynierskich.

Wprowadza się pojęcie uwarunkowania zadania, to znaczy jego podatności na zaburzenia danych. Dla przejrzystości, przypuśćmy, że nasze zadanie obliczeniowe polega na wyznaczeniu $f(x)$ dla danego $x$.

<flash>file=XXX.swf</flash><div.thumbcaption>Zadanie obliczeniowe i jego odporność na zaburzenia

Jak bardzo będzie odległe $f(\tilde{x})$, gdy $\tilde{x}\approx x$? Rozważa się dwa przypadki:

• uwarunkowanie względne: jak względne zaburzenie danych wpływa na błąd

względny wyniku:

$\frac{||f(x)-f(\tilde{x})||}{||f(x)||}\le {\text{cond}}_{rel}(f,x)\cdot \frac{||x-\tilde{x}||}{||x||}$

Najmniejszy mnożnik ${\text{cond}}_{rel}(f,x)$ spełniający powyższą nierówność nazywamy współczynnikiem uwarunkowania (względnego) zadania obliczenia $f(x)$ dla danego $x$.

• uwarunkowanie bezwzględne: jak bezwzględne zaburzenie danych wpływa na błąd

bezwzględny wyniku:

$||f(x)-f(\tilde{x})||\le {\text{cond}}_{abs}(f,x)\cdot ||x-\tilde{x}||$

Najmniejszy mnożnik ${\text{cond}}_{abs}(f,x)$ spełniający powyższą nierówność nazywamy współczynnikiem uwarunkowania (bezwzględnego) zadania obliczenia $f(x)$ dla danego $x$.

Powiemy, że zadanie jest

• dobrze uwarunkowane w punkcie $x$, gdy $\text{cond}(f,x)\approx 1$,
• źle uwarunkowane w punkcie $x$, gdy $\text{cond}(f,x)\gg 1$,
• źle postawione w punkcie $x$, gdy $\text{cond}(f,x)=+\mathrm{\infty }$.

Teraz już rozumiemy, że redukcja cyfr przy odejmowaniu jest tylko odzwierciedleniem faktu, że zadanie odejmowania dwóch bliskich liczb jest po prostu zadaniem źle uwarunkowanym!

Przykład: Uwarunkowanie zadania obliczenia sumy

Właściwie już wcześniej sprawdziliśmy, że zadanie obliczenia $s(x,y)=x+y$ ma

${\text{cond}}_{abs}(s,(a,b))=1,{\text{cond}}_{rel}(s,(a,b))=\frac{|a|+|b|}{|a+b|}$

Tak więc, gdy $a\approx -b$, to ${\text{cond}}_{rel}(s,(a,b))\approx +\mathrm{\infty }$ i zadanie jest bardzo źle uwarunkowane. Nawet małe zaburzenie względne danych może skutkować bardzo dużym zaburzeniem wyniku. Zgodnie z prawem Murphy'ego, najczęściej rzeczywiście tak będzie...

Przykład

Dla różniczkowalnej funkcji skalarnej $f:R\to R$ mamy

$|f(x)-f(\tilde{x}|\approx |f^{\prime }(x)||x-\tilde{x}|$

i w konsekwencji dla zadania obliczenia $f(x)$ dla danego $x$ mamy, przy założeniu małych zaburzeń,

${\text{cond}}_{abs}(f,x)=|f^{\prime }(x)|,{\text{cond}}_{rel}(f,x)=\frac{|f^{\prime }(x)|\cdot |x|}{|f(x)|}.$

Możnaby myśleć, że złe uwarunkowanie zawsze jest szkodliwe w praktyce numerycznej. Najczęściej właśnie tak jest istotnie. Jednak w praktyce numerycznej sporadycznie zdarza się, że Dodaj link: złe uwarunkowanie pewnego podzadania nie tylko nie pogarsza sytuacji, ale wręcz pomaga szybciej rozwiązać zadanie główne!

Rozkład algorytmu względem informacji

Algorytm to dokładnie określona i dozwolona w danym modelu obliczeniowym sekwencja akcji, pozwalająca na rozwiązanie danego zadania (w sposób dokładny lub przybliżony).

Z każdym algorytmem związany jest operator

Parser nie mógł rozpoznać (nieznana funkcja „\longrightarrowG”): {\displaystyle \displaystyle {\bf ALG}:\,F\longrightarrowG, }

taki że $\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f)$ jest wynikiem działania algorytmu w arytmetyce idealnej dla danej $f$.

Zauważmy, że wynik $\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f)$ działania algorytmu nie zależy bezpośrednio od $f$, ale raczej od informacji o $f$ (uzyskanej dzięki poleceniu ${ℐ}{𝒩}$). Informacja ta może być pełna albo tylko częściowa. Informacja jest pełna gdy, np. Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle f=(f_1,\ldots,f_n)\inR^n} i wczytamy wszystkie współrzędne $f_i$. Informacja może być częściowa, gdy $f$ jest funkcją. Wtedy wiele danych może posiadać tę samą informację, co łatwo zaobserwować na przykładzie zadania całkowania.

Niech Parser nie mógł rozpoznać (nieznana funkcja „\inftyR”): {\displaystyle \displaystyle N:F\to\cup_{n=0}^\inftyR^n} będzie operatorem informacji, tzn.

$N(f)=(y_1,y_2,\dots ,y_n)$

jest informacją o $f$ zebraną przy idealnej realizacji algorytmu. Zauważmy, że nformacja jest pełna gdy $N$ jest przekształceniem różnowartościowym, tzn. jeśli Parser nie mógł rozpoznać (nieznana funkcja „\nef”): {\displaystyle \displaystyle f_1\nef_2} implikuje Parser nie mógł rozpoznać (nieznana funkcja „\neN”): {\displaystyle \displaystyle N(f_1)\neN(f_2)} . W przeciwnym przypadku mamy do czynienia z informacją częściową.

Każdy algorytm $\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}$ może być przedstawiony jako złożenie operatora informacji i pewnego operatora Parser nie mógł rozpoznać (nieznana funkcja „\toG”): {\displaystyle \displaystyle \varphi:N(F)\toG} zdefiniowanego równością

$\phi (N(f))=\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f).$

Zauważmy, że w przypadku informacji częściowej zwykle nie istnieje algorytm dający dokładne rozwiązanie zadania dla każdej danej Parser nie mógł rozpoznać (nieznana funkcja „\inF”): {\displaystyle \displaystyle f\inF} , ponieważ dla danych o tej samej informacji mogą istnieć różne rozwiązania.

Problem wyboru algorytmu

Wybór algorytmu jest najistotniejszą częścią całego procesu numerycznego rozwiązywania zadania. Kierujemy się przy tym przede wszystkim następującymi kryteriami:

• dokładnością algorytmu,
• złożonością algorytmu,
• własnościami numerycznymi algorytmu.

Przez dokładność algorytmu rozumiemy różnicę między rozwiązaniem dokładnym $S(f)$, a rozwiązaniem $\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f)$ dawanym przez algorytm w arytmetyce idealnej. Jeśli $\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f)=S(f)$, $\mathrm{\forall }f\in F$, to algorytm nazywamy dokładnym.

Mówiąc o złożoności, mamy na myśli złożoność pamięciową (zwykle jest to liczba stałych i zmiennych używanych przez algorytm), jak również złożoność obliczeniową. Na złożoność obliczeniową algorytmu dla danej $f$ składa się koszt uzyskania infomacji $y=N(f)$ (zwykle jest on proporcjonalny do liczby wywołań polecenia ${ℐ}{𝒩}$), oraz koszt kombinatoryczny przetworzenia tej informacji, aż do uzyskania wyniku $\phi (y)$. Koszt kombinatoryczny zwykle mierzymy liczbą operacji arytmetycznych wykonywanych przez algorytm.

Przez własności numeryczne algorytmu rozumiemy jego własności przy realizacji w arytmetyce $f{l}_{\nu }$. Temu ważnemu tematowi poświęcimy teraz osobny paragraf.

Numeryczna poprawność algorytmu

Pożądane jest, aby algorytm dawał "dobry" wynik zarówno w arytmetyce idealnej, jak i w arytmetyce $f{l}_{\nu }$. Niestety, jak zobaczymy, nie zawsze jest to możliwe. Nawet jeśli algorytm jest dokładny to w wyniku jego realizacji w $f{l}_{\nu }$ możemy otrzymać wynik $f{l}_{\nu }(\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f))$ daleko odbiegający od $S(f)$. W szczególności, prawie zawsze mamy

$S(f)\ne f{l}_{\nu }(\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f)).$

Zauważmy również, że o ile z reguły znamy dokładne zachowanie się algorytmu w arytmetyce idealnej dla danej informacji, to nie można tego samego powiedzieć o jego zachowaniu się w arytmetyce $f{l}_{\nu }$. W związku z tym powstaje pytanie, jak kontrolować błąd algorytmów wynikający z błędów zaokrągleń i jakie algorytmy uznamy za te o najwyższej jakości numerycznej.

Istnienie błędów reprezentacji liczb rzeczywistych powoduje, że informacja $y=N(f)$ o danej $f$ nie jest w ogólności reprezentowana dokładnie. Znaczy to, że zamiast na informacji dokładnej, dowolny algorytm będzie operować na informacji nieco zaburzonej $y_{\nu }$, tzn. zaburzonej na poziomie błędu reprezentacji. Tak samo wynik dawany przez algorytm będzie w ogólności zaburzony na poziomie błędu reprezentacji. W najlepszym więc wypadku wynikiem działania algorytmu w $f{l}_{\nu }$ będzie $(\phi (y_{\nu }){)}_{\nu }$ zamiast $\phi (y)$. Algorytmy dające tego rodzaju wyniki uznamy za posiadające najlepsze własności numeryczne w arytmetyce $f{l}_{\nu }$ i nazwiemy numerycznie poprawnymi.

Dokładniej, powiemy, że ciąg rzeczywisty $a_{\nu }=(a_{\nu ,1},\dots ,a_{\nu ,n})$ (a właściwie rodzina ciągów $\{a_{\nu }{\}}_{\nu }$) jest nieco zaburzonym ciągiem $a=(a_1,\dots ,a_n)$, jeśli istnieje stała $K$ taka, że dla wszystkich dostatecznie małych $\nu$ zachodzi

$|a_{\nu ,j}-a_j|\le K\nu |a_j|,1\le j\le n,$

albo ogólniej

$\Vert a_{\nu }-a\Vert \le K\nu \Vert a\Vert ,$

gdzie $\Vert \cdot \Vert$ jest pewną normą w $R^n$. W pierwszym przypadku mówimy o zaburzeniu "po współrzędnych", a w drugim o zaburzeniu w normie $\Vert \cdot \Vert$.

Zauważmy, że niewielkie zaburzenia po współrzędnych pociągają za sobą niewielkie zaburzenia w normie. Rzeczywiście, zachodzi wówczas

$\Vert a_{\nu }-a{\Vert }_{\mathrm{\infty }}=\underset{1\le j\le n}{\max }|a_{\nu ,j}-a_j|\le K\nu \underset{1\le j\le n}{\max }|a_j|=K\nu \Vert a{\Vert }_{\mathrm{\infty }},$

i korzystając z faktu, że w przestrzeni skończenie wymiarowej wszystkie normy są równoważne otrzymujemy dla pewnych stałych $K_1$ i $K_2$

$\Vert a_{\nu }-a\Vert \le K_1\Vert a_{\nu }-a{\Vert }_{\mathrm{\infty }}\le K_{1}K\nu \Vert a{\Vert }_{\mathrm{\infty }}\le K_2{K}_{1}K\nu \Vert a\Vert ,$

czyli nierówność dla zaburzenia w normie, ze stałą $K=K_2{K}_{1}K$.

Definicja Algorytm numerycznie poprawny

Algorytm $\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}$ rozwiązywania zadania nazywamy numerycznie poprawnym w zbiorze danych Parser nie mógł rozpoznać (nieznana funkcja „\subsetF”): {\displaystyle \displaystyle F_0\subsetF} , jeśli dla każdej danej Parser nie mógł rozpoznać (nieznana funkcja „\inF”): {\displaystyle \displaystyle f\inF_0} wynik $f{l}_{\nu }(\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f))$ działania algorytmu w arytmetyce $f{l}_{\nu }$ można zinterpretować jako nieco zaburzony wynik algorytmu w arytmetyce idealnej dla nieco zaburzonej informacji Parser nie mógł rozpoznać (nieznana funkcja „\inN”): {\displaystyle \displaystyle y_\nu=(N(f))_\nu\inN(F)} o $f$, przy czym poziom zaburzeń nie zależy od $f$.

Formalnie znaczy to, że istnieją stałe $K_1$, $K_2$, oraz ${\nu }_0>0$ takie, że spełniony jest następujący warunek. Dla dowolnej $\nu \le {\nu }_0$ oraz informacji Parser nie mógł rozpoznać (nieznana funkcja „\inN”): {\displaystyle \displaystyle y\inN(F_0)} można dobrać Parser nie mógł rozpoznać (nieznana funkcja „\inN”): {\displaystyle \displaystyle y_\nu\inN(F)} oraz ${(\phi (y_{\nu }))}_{\nu }$ takie, że

$\Vert y_{\nu }-y\Vert \le K_1\nu \Vert y\Vert ,$ $\Vert {(\phi (y_{\nu }))}_{\nu }-\phi (y_{\nu })\Vert \le K_2\nu \Vert \phi (y_{\nu })\Vert ,$

oraz

$f{l}_{\nu }(\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f))=f{l}_{\nu }(\phi (N(f)))={(\phi (y_{\nu }))}_{\nu }.$

Numerycznie poprawny algorytm daje w arytmetyce $f{l}_{\nu }$ wynik $ALG(N(x))$, który daje się zinterpretować jako mało zaburzony wynik $f(y)$ zadania na mało zaburzonych danych $x$.

Zauważmy,że jeśli Parser nie mógł rozpoznać (nieznana funkcja „\inR”): {\displaystyle \displaystyle f\inR^n} , $N(f)=(f_1,\dots ,f_n)$, oraz algorytm jest dokładny, Parser nie mógł rozpoznać (nieznana funkcja „\equivS”): {\displaystyle \displaystyle {\bf ALG}\equiv\varphi\equivS} , to numeryczną poprawność algorytmu można równoważnie zapisać jako

$f{l}_{\nu }(\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f))={(S(f_{\nu }))}_{\nu }.$

Rola uwarunkowania zadania

Niech $\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(\cdot )=\phi (N(\cdot ))$ będzie algorytmem numerycznie poprawnym dla danych Parser nie mógł rozpoznać (nieznana funkcja „\subsetF”): {\displaystyle \displaystyle F_0\subsetF} . Wtedy jego błąd w $f{l}_{\nu }$ można oszacować następująco:

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \lefteqn{ \|S(f)-fl_\nu({\bf ALG}(f))\| \;=\; \|S(f)-\left(\varphi(y_\nu)\right)_\nu\| } \\ &\le & \|S(f)-\varphi(y)\|\,+\, \|\varphi(y)-\varphi(y_\nu)\|\,+\, \|\varphi(y_\nu)-\left(\varphi(y_\nu)\right)_\nu\| \\ &\le & \|S(f)-{\bf ALG}(f)\|\,+\, \|\varphi(y)-\varphi(y_\nu)\|\,+\, K_2\,\nu\,\|\varphi(y_\nu)\| \\ &\le & \|S(f)-{\bf ALG}(f)\|\,+\, (1 + K_2 \nu) \|\varphi(y)-\varphi(y_\nu)\|\,+\, K_2\,\nu\,\|\varphi(y)\|, \endaligned}

przy czym $\Vert y_{\nu }-y\Vert \le K_1\nu \Vert y\Vert$. Stąd w szczególności wynika, że jeśli algorytm jest numerycznie poprawny i ciągły ze względu na informację $y$, to

$\underset{\nu \to 0}{\lim }\Vert S(f)-f{l}_{\nu }(\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f))\Vert =\Vert S(f)-\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f)\Vert .$

To znaczy, że dla dostatecznie silnej arytmetyki algorytm będzie się zachowywał w $f{l}_{\nu }$ prawie tak jak w arytmetyce idealnej.

Z powyższych wzorów wynika, że błąd w $f{l}_{\nu }$ algorytmu numerycznie poprawnego zależy w dużym stopniu od:

• dokładności algorytmu w arytmetyce idealnej,
• dokładności $\nu$ arytmetyki $f{l}_{\nu }$,
• wrażliwości algorytmu na małe względne zaburzenia informacji $y$.

Ponieważ dwa pierwsze punkty są raczej oczywiste, poświęcimy trochę więcej uwagi jedynie trzeciemu.

Jeśli $\phi$ spełnia warunek Lipschitza ze stałą $L$, a dokładniej

$\Vert \phi (y_{\nu })-\phi (y)\Vert \le L\Vert y_{\nu }-y\Vert ,$

to

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \lefteqn{ \|S(f)-fl_\nu({\bf ALG}(f))\|} \\ &\le & \|S(f)-{\bf ALG}(f)\|\,+\, (1+K_2\nu)L\|y_\nu-y\|\,+\,K_2\nu\|\varphi(y)\| \\ &\le & \|S(f)-{\bf ALG}(f)\|\,+\, (1+K_2\nu)LK_1\nu\|y\|\,+\,K_2\nu\|\varphi(y)\|. \endaligned}

W tym przypadku błędy zaokrągleń zwiększają błąd bezwzględny algorytmu proporcjonalnie do $\nu$.

Bardziej jednak interesuje nas błąd względny. Wybierzmy "małe" $\eta \ge 0$ i przypuśćmy, że

$\Vert \phi (y_{\nu })-\phi (y)\Vert \le M{K}_1\nu \max (\eta ,\Vert \phi (y)\Vert ),$

dla pewnej $M$ niezależnej od $y$, tzn. błąd względny informacji, $\Vert y_{\nu }-y\Vert \le K_1\nu \Vert y\Vert$, przenosi się na błąd względny wyniku (w arytmetyce idealnej) ze "współczynnikiem wzmocnienia" $M$, albo na błąd bezwzględny ze współczynnikiem $M\eta$. (Zauważmy, że gdybyśmy wzięli $\eta =0$ to dla $y$ takiej, że $\phi (y)=0$ musiałoby być $\phi (y_{\nu })=0$, co zwykle, choć nie zawsze, nie jest prawdą.) Wtedy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \|S(f)-fl_\nu({\bf ALG}(f))\| & \le & \|S(f)-{\bf ALG}(f)\|+ (1 + K_2 \nu) M K_1 \nu \max (\eta, \|\varphi(y)\|)+ K_2 \nu \|\varphi(y)\| \\ &= \|S(f)-{\bf ALG}(f)\|\,+\,\nu\, \Big(\,MK_1(1+K_2\nu)+K_2\Big)\max(\eta,\|\varphi(y)\|). \endaligned}

W szczególności, gdy algorytm jest dokładny i korzysta z pełnej informacji o $f$, tzn. $S\equiv \mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}\equiv \phi$, to błąd

$\frac{\Vert S(f)-f{l}_{\nu }(\mathbf{𝐀}\mathbf{𝐋}\mathbf{𝐆}(f))\Vert }{\max (\eta ,\Vert S(f)\Vert )}\le (M{K}_1(1+K_2\nu )+K_2)\nu \approx (M{K}_1+K_2)\nu .$

Stąd wynika, że jeśli $(M{K}_1+K_2)\nu \ll 1$ to błąd względny algorytmu w $f{l}_{\nu }$ jest mały, o ile $\Vert S(f)\Vert \ge \eta$. Błąd względny jest proporcjonalny do dokładności $\nu$, arytmetyki $f{l}_{\nu }$, współczynników proporcjonalności $K_i$ algorytmu numerycznie poprawnego, oraz do wrażliwości $M$ zadania $S$ na małe względne zaburzenia danych.

Zwróćmy uwagę na istotny fakt, że interesują nas właściwie tylko te zaburzenia danych (informacji), które powstają przy analizie algorytmu numerycznie poprawnego. I tak, jeśli algorytm jest numerycznie poprawny z pozornymi zaburzeniami danych w normie, to trzeba zbadać wrażliwość zadania ze względu na zaburzenia danych w normie. Jeśli zaś mamy pozorne zaburzenia "po współrzędnych" (co oczywiście implikuje pozorne zaburzenia w normie) to wystarczy zbadać uwarunkowanie zadania ze względu na zaburzenia "po współrzędnych", itd.

Przykład: Iloczyn skalarny

Załóżmy. że dla danych ciągów rzeczywistych o ustalonej długości $n$, $a_j$, $b_j$, $1\le j\le n$, chcemy obliczyć

$S(a,b)=\sum _{j=1}^n{a}_j{b}_j.$

Rozpatrzymy algorytm dokładny zdefiniowany powyższym wzorem i korzystający z pełnej informacji o kolejnych współrzednych.

Oznaczmy przez ${\tilde{a}}_j$ i ${\tilde{b}}_j$ reprezentacje liczb $a_j$ i $b_j$ w $f{l}_{\nu }$, ${\tilde{a}}_j=a_j(1+{\alpha }_j)$, ${\tilde{b}}_j=b_j(1+{\beta }_j)$, oraz przez ${\gamma }_j$ i ${\delta }_j$ błędy względne powstałe przy kolejnych mnożeniach i dodawaniach. Oczywiście $|{\alpha }_j|,|{\beta }_j|,|{\gamma }_j|,|{\delta }_j|\le \nu$. Otrzymujemy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned fl_\nu\left(\sum_{j=1}^n a_jb_j\right) &= \Big(\,(fl_\nu(\sum_{j=1}^{n-1}a_jb_j)\,+\,\tilde a_n\tilde b_n (1+\gamma_n)\,\Big)(1+\delta_n)\,=\,\ldots \\ &= \bigg(\cdots\Big( \tilde a_1\tilde b_1(1+\gamma_1)+\tilde a_2\tilde b_2 (1+\gamma_2)\Big)(1+\delta_2) \\ & & \qquad\qquad\qquad\qquad +\cdots+ \tilde a_n\tilde b_n(1+\gamma_n)\bigg)(1+\delta_n) \\ &= \tilde a_1\tilde b_1(1+\gamma_1)(1+\delta_2) \cdots(1+\delta_n)\\ & & \qquad\qquad\qquad\qquad +\cdots+\tilde a_j \tilde b_j(1+\gamma_j)(1+\delta_j)\cdots(1+\delta_n) \\ &= \sum_{j=1}^n a_jb_j(1+e_j), \endaligned}

gdzie w przybliżeniu (tzn. gdy $\nu \to 0$) mamy $|e_1|\le (n+2)\nu$ i $|e_j|\le (n-j+4)\nu$, $2\le j\le n$. Algorytm naturalny jest więc numerycznie poprawny w całym zbiorze danych, gdyż wynik otrzymany w $f{l}_{\nu }$ można zinterpretować jako dokładny wynik dla danych $a_{\nu ,j}=a_j$ i $b_{\nu ,j}=b_j(1+e_j)$, przy czym $\Vert b_{\nu }-b{\Vert }_p\le (n+2)\nu \Vert b{\Vert }_p$.

Zobaczmy teraz, jak błąd we współrzędnych $b_j$ wpływa na błąd wyniku. Mamy

Parser nie mógł rozpoznać (nieznana funkcja „\aligned”): {\displaystyle \displaystyle \aligned \Big|\sum_{j=1}^n a_jb_j-fl_\nu\Big(\sum_{j=1}^n a_jb_j\Big)\Big| &= \Big|\sum_{j=1}^n a_jb_j-\sum_{j=1}^n a_jb_j(1+e_j)\Big| \\ &= \Big|\sum_{j=1}^n e_ja_jb_j\Big| \,\le\, \sum_{j=1}^n |e_j||a_jb_j| \\ &\leq (n+2)\nu\sum_{j=1}^n |a_jb_j|. \endaligned}

Stąd dla $\eta \ge 0$

$\frac{|\sum _{j=1}^n{a}_j{b}_j-f{l}_{\nu }(\sum _{j=1}^n{a}_j{b}_j)|}{\max (\eta ,|\sum _{j=1}^n{a}_j{b}_j|)}\le K_{\eta }(n+2)\nu ,$

gdzie

$K_{\eta }=K_{\eta }(a,b)=\frac{\sum _{j=1}^n|a_j{b}_j|}{\max (\eta ,|\sum _{j=1}^n{a}_j{b}_j|)}.$

Zauważmy, że jeśli iloczyny $a_j{b}_j$ są wszystkie dodatnie albo wszystkie ujemne, to $K_{\eta }=1$, tzn. zadanie jest dobrze uwarunkowane, a błąd względny jest zawsze na poziomie co najwyżej $n\nu$. W tym przypadku algorytm zachowuje się bardzo dobrze, o ile liczba $n$ składników nie jest horendalnie duża. W ogólności jednak $K_{\eta }$ może być liczbą dowolnie dużą i wtedy nie możemy być pewni uzyskania dobrego wyniku w $f{l}_{\nu }$.