ED-4.2-m14-1.0-Slajd23: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 4: | Linia 4: | ||
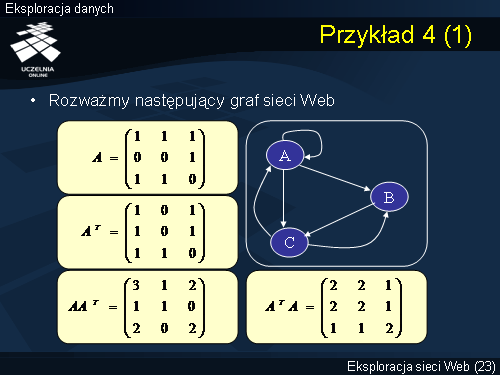
Dla ilustracji działania algorytmu H & A rozważmy prosty przykład przedstawiony na slajdzie. Załóżmy, że Web składa się z 3 stron: A, B, i C. Graf przedstawiony na slajdzie przedstawia strukturę połączeń pomiędzy stronami. Macierz A naszej uproszczonej sieci Web przedstawiono na slajdzie. Przykładowo, wiersz 1 macierzy A zawiera następujące elementy: 1, 1 i 1. Elementy A[1, 1] = A[1, 2] = A[1, 3] = 1, gdyż strona A (z numerem 1) posiada linki wychodzące do stron A, B (z numerem 2) i C (z numerem 3). Wiersz 2 macierzy A zawiera następujące elementy: 0, 0, i 1. Elementy A[2, 1] = A[2, 2] = 0, gdyż strona B nie posiada linków wychodzących do stron A i B, natomiast element A[2, 3] = 1, gdyż strona B posiada link wychodzący do strony C. Wreszcie, wiersz 3 macierzy A zawiera elementy: 1, 1, i 0. Elementy A[3, 1] = A[3, 2] = 1, gdyż strona C posiada linki wychodzące do stron A i B, natomiast element A[3, 3 | Dla ilustracji działania algorytmu H & A rozważmy prosty przykład przedstawiony na slajdzie. Załóżmy, że Web składa się z 3 stron: A, B, i C. Graf przedstawiony na slajdzie przedstawia strukturę połączeń pomiędzy stronami. Macierz A naszej uproszczonej sieci Web przedstawiono na slajdzie. Przykładowo, wiersz 1 macierzy A zawiera następujące elementy: 1, 1 i 1. Elementy A[1, 1] = A[1, 2] = A[1, 3] = 1, gdyż strona A (z numerem 1) posiada linki wychodzące do stron A, B (z numerem 2) i C (z numerem 3). Wiersz 2 macierzy A zawiera następujące elementy: 0, 0, i 1. Elementy A[2, 1] = A[2, 2] = 0, gdyż strona B nie posiada linków wychodzących do stron A i B, natomiast element A[2, 3] = 1, gdyż strona B posiada link wychodzący do strony C. Wreszcie, wiersz 3 macierzy A zawiera elementy: 1, 1, i 0. Elementy A[3, 1] = A[3, 2] = 1, gdyż strona C posiada linki wychodzące do stron A i B, natomiast element A[3, 3] = 0, gdyż strona C nie posiada linku do siebie. Na slajdzie przedstawiono również macierze: A(transponowane) oraz iloczyny macierzy A * A(transponowane) oraz A(transponowane)* A. | ||
[[ED-4.2-m14-1.0-Slajd22 | << Poprzedni slajd]] | [[ED-4.2-m14-1.0-toc|Spis treści ]] | [[ED-4.2-m14-1.0-Slajd24 | Następny slajd >>]] | [[ED-4.2-m14-1.0-Slajd22 | << Poprzedni slajd]] | [[ED-4.2-m14-1.0-toc|Spis treści ]] | [[ED-4.2-m14-1.0-Slajd24 | Następny slajd >>]] | ||
Aktualna wersja na dzień 13:12, 31 sie 2006
Przykład 4 (1)
Dla ilustracji działania algorytmu H & A rozważmy prosty przykład przedstawiony na slajdzie. Załóżmy, że Web składa się z 3 stron: A, B, i C. Graf przedstawiony na slajdzie przedstawia strukturę połączeń pomiędzy stronami. Macierz A naszej uproszczonej sieci Web przedstawiono na slajdzie. Przykładowo, wiersz 1 macierzy A zawiera następujące elementy: 1, 1 i 1. Elementy A[1, 1] = A[1, 2] = A[1, 3] = 1, gdyż strona A (z numerem 1) posiada linki wychodzące do stron A, B (z numerem 2) i C (z numerem 3). Wiersz 2 macierzy A zawiera następujące elementy: 0, 0, i 1. Elementy A[2, 1] = A[2, 2] = 0, gdyż strona B nie posiada linków wychodzących do stron A i B, natomiast element A[2, 3] = 1, gdyż strona B posiada link wychodzący do strony C. Wreszcie, wiersz 3 macierzy A zawiera elementy: 1, 1, i 0. Elementy A[3, 1] = A[3, 2] = 1, gdyż strona C posiada linki wychodzące do stron A i B, natomiast element A[3, 3] = 0, gdyż strona C nie posiada linku do siebie. Na slajdzie przedstawiono również macierze: A(transponowane) oraz iloczyny macierzy A * A(transponowane) oraz A(transponowane)* A.