PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 11: | Linia 11: | ||
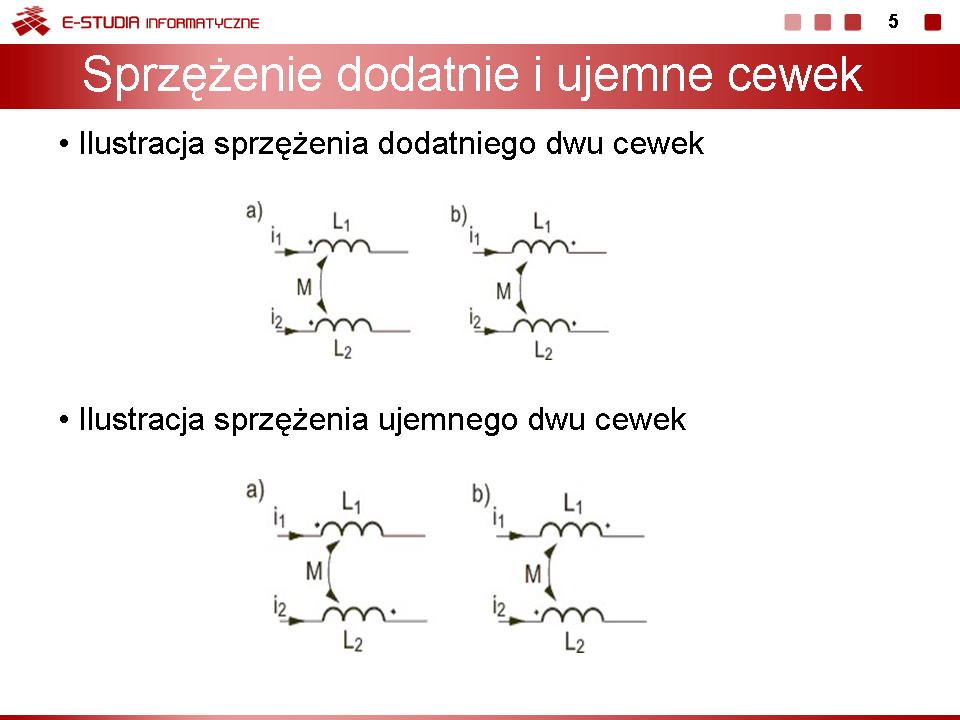
Przyjmijmy, że dwie cewki są położone blisko siebie w taki sposób, że strumień magnetyczny jednej cewki przenika również drugą. Całkowity strumień skojarzony z daną cewką (strumień skojarzony jest sumą strumieni <math>\phi\,</math> każdego zwoju cewki, co przy z zwojach o identycznym strumieniu daje <math>\psi=z\phi</math> jest wtedy sumą obu strumieni, jeśli ich kierunki są zgodne lub ich różnicą, jeśli kierunki strumieni są przeciwne. Strumienie obu cewek zapiszemy wówczas w postaci. | Przyjmijmy, że dwie cewki są położone blisko siebie w taki sposób, że strumień magnetyczny jednej cewki przenika również drugą. Całkowity strumień skojarzony z daną cewką (strumień skojarzony jest sumą strumieni <math>\phi\,</math> każdego zwoju cewki, co przy z zwojach o identycznym strumieniu daje <math>\psi=z\phi</math> jest wtedy sumą obu strumieni, jeśli ich kierunki są zgodne lub ich różnicą, jeśli kierunki strumieni są przeciwne. Strumienie obu cewek zapiszemy wówczas w postaci. | ||
<math>\psi_1=\psi_1_1\pm\psi_1_2</math> | <math>\psi_1=\psi_1_1\pm\psi_1_2</math> | ||
| Linia 21: | Linia 20: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd3.png]] | ||
|valign="top"|Strumień <math>\psi_1_1</math> występujący w cewce pierwszej pochodzi od prądu tej cewki a strumień | |valign="top"|Strumień <math>\psi_1_1</math> występujący w cewce pierwszej pochodzi od prądu tej cewki a strumień <math>\psi_2_1</math> jest wytworzony przez cewkę drugą i przenika przez cewkę pierwszą. Podobnie strumień <math>\psi_2_2</math> pojawiający się w cewce drugiej pochodzi od prądu tej cewki a strumień <math>\psi_1_2</math> pochodzący od prądu cewki pierwszej przenika przez cewkę drugą. Uwzględniając pojęcie indukcyjności własnej i wzajemnej wprowadzone w rozdziale pierwszym dla cewek liniowych sprzężonych magnetycznie obowiązują następujące relacje: | ||
*'''Indukcyjności własne''' | |||
: <math>L_1=\frac{\psi_{11}}{i_1}</math>, <math>L_2=\frac{\psi_{22}}{i_2}</math> | |||
*Indukcyjności wzajemne | *'''Indukcyjności wzajemne''' | ||
: <math>M_{12}=\frac{\psi_{12}}{i_2}</math>, <math>M_{21}=\frac{\psi_{21}}{i_1}</math> | |||
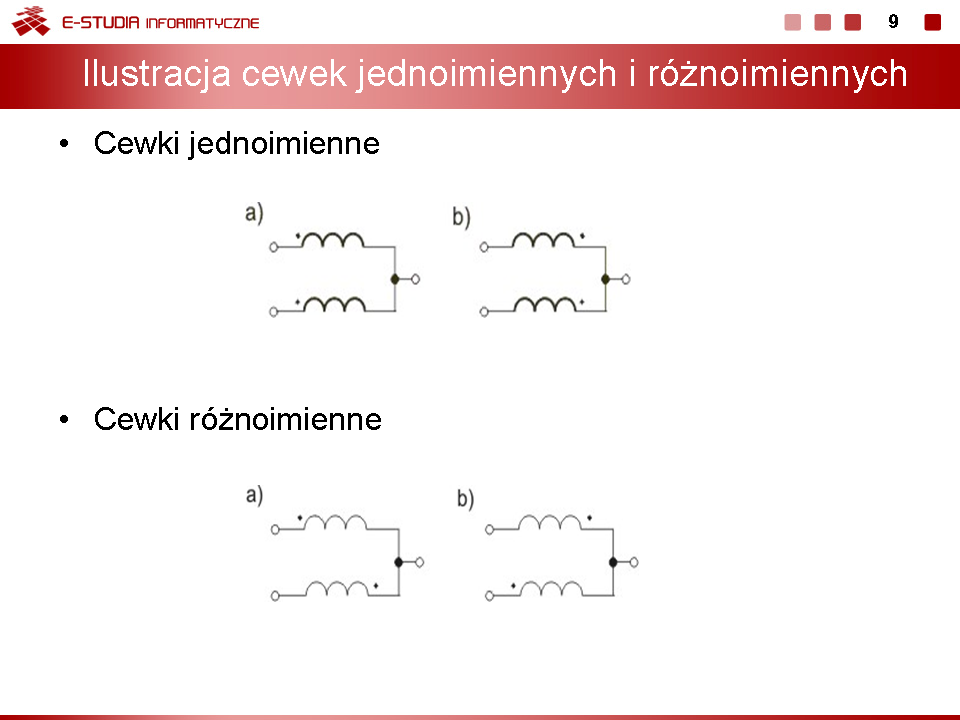
Dla środowisk o tej samej przenikalności magnetycznej obie indukcyjności wzajemne są sobie równe, to znaczy <math>M_1_2=M_2_1=M</math> Dla dwu cewek sprzężonych magnetycznie definiuje się '''współczynnik sprzężenia''' jako średnią geometryczną współczynników sprzężenia obu cewek, przy czym współczynnik sprzężenia jednej cewki z drugą jest określany jako stosunek strumienia głównego cewki pochodzącego od prądu własnego do strumienia całkowitego cewki. Współczynnik sprzężenia cewek oznaczać będziemy literą <math>k\,</math>. Spełnia on następującą relację | Dla środowisk o tej samej przenikalności magnetycznej obie indukcyjności wzajemne są sobie równe, to znaczy <math>M_1_2=M_2_1=M</math> Dla dwu cewek sprzężonych magnetycznie definiuje się '''współczynnik sprzężenia''' jako średnią geometryczną współczynników sprzężenia obu cewek, przy czym współczynnik sprzężenia jednej cewki z drugą jest określany jako stosunek strumienia głównego cewki pochodzącego od prądu własnego do strumienia całkowitego cewki. Współczynnik sprzężenia cewek oznaczać będziemy literą <math>k\,</math>. Spełnia on następującą relację | ||
<math>M=k\sqrt{L_1L_2}</math> | : <math>M=k\sqrt{L_1L_2}</math> | ||
Przy idealnym (pełnym) sprzężeniu cewek wartość współczynnika sprzężenia jest równa jeden (k=1). Indukcyjność wzajemna jest wówczas średnią geometryczną indukcyjności własnych obu cewek. Przy braku sprzężenia magnetycznego między cewkami wartość k=0. | Przy idealnym (pełnym) sprzężeniu cewek wartość współczynnika sprzężenia jest równa jeden (k=1). Indukcyjność wzajemna jest wówczas średnią geometryczną indukcyjności własnych obu cewek. Przy braku sprzężenia magnetycznego między cewkami wartość k=0. | ||
| Linia 45: | Linia 47: | ||
<math>u_1=\frac{d\psi_1}{dt} = L_1\frac{di_1}{dt}\pm M\frac{di_2}{dt}</math> | : <math>u_1=\frac{d\psi_1}{dt} = L_1\frac{di_1}{dt}\pm M\frac{di_2}{dt}</math> | ||
<math>u_2=\frac{d\psi_2}{dt} = L_2\frac{di_2}{dt}\pm M\frac{di_1}{dt}</math> | : <math>u_2=\frac{d\psi_2}{dt} = L_2\frac{di_2}{dt}\pm M\frac{di_1}{dt}</math> | ||
| Linia 75: | Linia 77: | ||
Analiza obwodów ze sprzężeniami magnetycznymi w stanie ustalonym przy wymuszeniu sinusoidalnym może być przeprowadzona przy zastosowaniu metody symbolicznej, w której w miejsce różniczkowania wprowadza się działania na liczbach zespolonych. Dla wymuszenia sinusoidalnego wzory różniczkowe upraszczają się do zależności algebraicznych typu zespolonego, które podobnie jak dla indukcyjności własnych wyprowadzonych w rozdziale drugim można zapisać w postaci | Analiza obwodów ze sprzężeniami magnetycznymi w stanie ustalonym przy wymuszeniu sinusoidalnym może być przeprowadzona przy zastosowaniu metody symbolicznej, w której w miejsce różniczkowania wprowadza się działania na liczbach zespolonych. Dla wymuszenia sinusoidalnego wzory różniczkowe upraszczają się do zależności algebraicznych typu zespolonego, które podobnie jak dla indukcyjności własnych wyprowadzonych w rozdziale drugim można zapisać w postaci | ||
<math>U_1=j\omega L_1I_1\pm j\ | : <math>U_1=j\omega L_1I_1\pm j\omega MI_2</math> | ||
<math>U_2=j\omega L_2I_2\pm j\ | : <math>U_2=j\omega L_2I_2\pm j\omega MI_1</math> | ||
Znak plus obowiązuje dla '''sprzężenia dodatniego''' (strumienie magnetyczne obu cewek sumują się) a znak minus dla '''sprzężenia ujemnego''' (strumienie magnetyczne obu cewek odejmują się). Jak widać z powyższych wzorów cewki sprzężone magnetycznie reprezentują sobą reaktancje, przy czym można tu wyróżnić dwa rodzaje reaktancji: '''reaktancję indukcyjną własną''' (zwaną dotąd reaktancją indukcyjną) i '''reaktancję indukcyjną wzajemną'''. Wprowadźmy następujące oznaczenia | Znak plus obowiązuje dla '''sprzężenia dodatniego''' (strumienie magnetyczne obu cewek sumują się) a znak minus dla '''sprzężenia ujemnego''' (strumienie magnetyczne obu cewek odejmują się). Jak widać z powyższych wzorów cewki sprzężone magnetycznie reprezentują sobą reaktancje, przy czym można tu wyróżnić dwa rodzaje reaktancji: '''reaktancję indukcyjną własną''' (zwaną dotąd reaktancją indukcyjną) i '''reaktancję indukcyjną wzajemną'''. Wprowadźmy następujące oznaczenia | ||
<math>X_M=\omega M</math> reaktancja | : <math>X_M=\omega M</math> reaktancja indukcyjna wzajemna | ||
: <math>Z_M=j\omega M</math> impedancja indukcyjna wzajemna | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 95: | Linia 95: | ||
<math>U_1=Z_{L1}I_1\pm Z_MI_2=j\omega L_1I_1\pm j\omega MI_2</math> | : <math>U_1=Z_{L1}I_1\pm Z_MI_2=j\omega L_1I_1\pm j\omega MI_2</math> | ||
<math>U_2=Z_{L1}I_2\pm Z_MI_1=j\omega L_2I_2\pm j\omega MI_1</math> | : <math>U_2=Z_{L1}I_2\pm Z_MI_1=j\omega L_2I_2\pm j\omega MI_1</math> | ||
| Linia 181: | Linia 181: | ||
Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu: | Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu: | ||
<math>I=\frac{5}{\sqrt2}e^{j45^o}</math> | : <math>I=\frac{5}{\sqrt2}e^{j45^o}</math> | ||
<math>Z_1=j\omega(L_1-M)=j1</math> | : <math>Z_1=j\omega(L_1-M)=j1</math> | ||
<math>Z_2=j\omega(L_2-M)=0</math> | : <math>Z_2=j\omega(L_2-M)=0</math> | ||
<math>Z_M=j\omega M=j1</math> | : <math>Z_M=j\omega M=j1</math> | ||
Impedancja zastępcza obwodu wobec <math>Z_2=0</math> | Impedancja zastępcza obwodu wobec <math>Z_2=0</math> | ||
<math>Z=\frac{RZ_M}{R+Z_M}=\frac{1}{\sqrt2}e^{j45^o}</math> | : <math>Z=\frac{RZ_M}{R+Z_M}=\frac{1}{\sqrt2}e^{j45^o}</math> | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 202: | Linia 201: | ||
|valign="top"|Napięcie <math>U_{AB}\,</math> | |valign="top"|Napięcie <math>U_{AB}\,</math> | ||
<math>U_{AB}=ZI=j5</math> | : <math>U_{AB}=ZI=j5</math> | ||
Prądy: | Prądy: | ||
<math>I_R=\frac{U_{AB}}{R}=j5</math> | : <math>I_R=\frac{U_{AB}}{R}=j5</math> | ||
<math>I_1=0</math> | : <math>I_1=0</math> | ||
<math>I_2=I_3\frac{U_{AB}}{Z_M}=5</math> | : <math>I_2=I_3\frac{U_{AB}}{Z_M}=5</math> | ||
Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą <math>U_{AB}=j5</math>. Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie | Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą <math>U_{AB}=j5</math>. Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie | ||
<math>U_{L_1}=j\omega L_1I_1+j\omega MI_2=j5</math> | : <math>U_{L_1}=j\omega L_1I_1+j\omega MI_2=j5</math> | ||
<math>U_{L_2}=j\omega L_2I_2+j\omega MI_1=j5</math> | : <math>U_{L_2}=j\omega L_2I_2+j\omega MI_1=j5</math> | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 231: | Linia 229: | ||
W analizie teoretycznej przyjmować będziemy transformator idealizowany, czyli taki w którym nie ma strat energii, nie istnieje zjawisko rozpraszania strumienia magnetycznego (współczynnik sprzężenia magnetycznego k=1), nie występują efekty pasożytnicze (np. pojemności międzyzwojowe), nie uwzględniona jest rezystancja uzwojeń, zjawiska prądów wirowych itp. | W analizie teoretycznej przyjmować będziemy transformator idealizowany, czyli taki w którym nie ma strat energii, nie istnieje zjawisko rozpraszania strumienia magnetycznego (współczynnik sprzężenia magnetycznego k=1), nie występują efekty pasożytnicze (np. pojemności międzyzwojowe), nie uwzględniona jest rezystancja uzwojeń, zjawiska prądów wirowych itp. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 244: | Linia 239: | ||
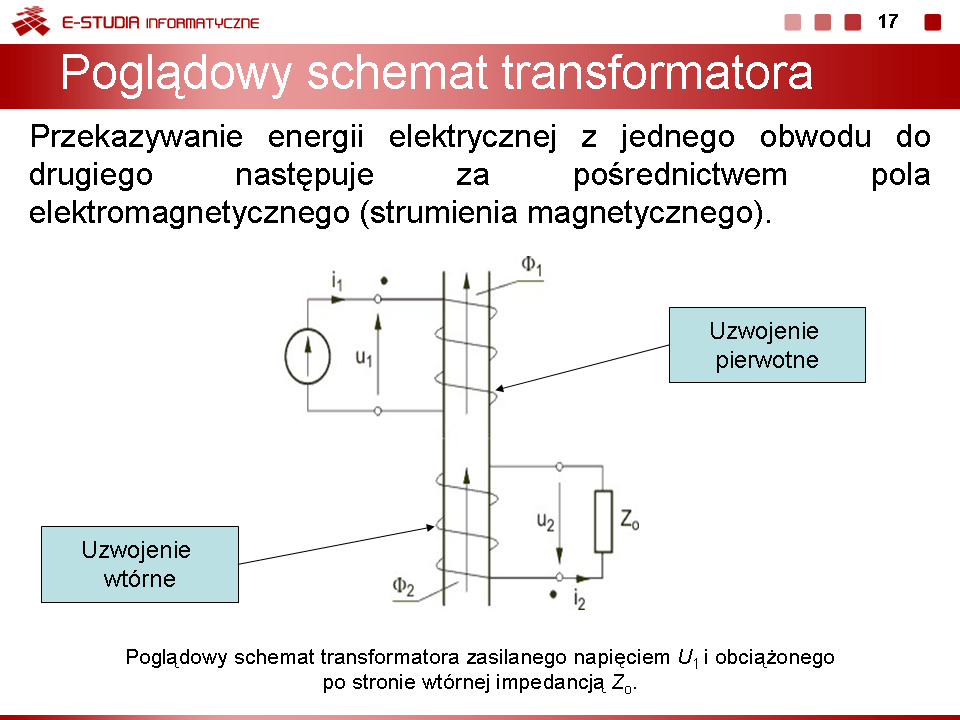
Do uzwojenia pierwotnego przyłożone jest napięcie sinusoidalnie zmienne o wartości chwilowej <math>u_1(t)\,</math>. Wartość chwilową prądu w uzwojeniu pierwotnym oznaczymy przez <math>i_1(t)\,</math>. Pod wpływem zmiennego w czasie prądu <math>i_1(t)\,</math> w przestrzeni otaczającej uzwojenie powstaje zmienny strumień magnetyczny <math>\phi\,</math>, będący superpozycją strumieni <math>\phi_1</math> i <math>\phi_2</math>. Przy założeniu jego równomiernego rozkładu na przekroju <math>S</math>, strumień jest iloczynem indukcji magnetycznej <math>B</math> i przekroju <math>S</math>, <math>\phi = BS</math>. Strumień ten kojarzy się zarówno z uzwojeniem pierwotnym o liczbie zwojów <math>z_1\,</math> wytwarzając strumień skojarzony <math>\psi_1=z_1\phi</math>, jak i uzwojeniem wtórnym o liczbie zwojów z2 wytwarzając w nim strumień skojarzony <math>\psi_2=z_2\phi</math> Zgodne z prawem indukcji elektromagnetycznej pod wpływem zmiennego w czasie strumienia magnetycznego indukuje się napięcie <math>u(t)\,</math> | Do uzwojenia pierwotnego przyłożone jest napięcie sinusoidalnie zmienne o wartości chwilowej <math>u_1(t)\,</math>. Wartość chwilową prądu w uzwojeniu pierwotnym oznaczymy przez <math>i_1(t)\,</math>. Pod wpływem zmiennego w czasie prądu <math>i_1(t)\,</math> w przestrzeni otaczającej uzwojenie powstaje zmienny strumień magnetyczny <math>\phi\,</math>, będący superpozycją strumieni <math>\phi_1</math> i <math>\phi_2</math>. Przy założeniu jego równomiernego rozkładu na przekroju <math>S</math>, strumień jest iloczynem indukcji magnetycznej <math>B</math> i przekroju <math>S</math>, <math>\phi = BS</math>. Strumień ten kojarzy się zarówno z uzwojeniem pierwotnym o liczbie zwojów <math>z_1\,</math> wytwarzając strumień skojarzony <math>\psi_1=z_1\phi</math>, jak i uzwojeniem wtórnym o liczbie zwojów z2 wytwarzając w nim strumień skojarzony <math>\psi_2=z_2\phi</math> Zgodne z prawem indukcji elektromagnetycznej pod wpływem zmiennego w czasie strumienia magnetycznego indukuje się napięcie <math>u(t)\,</math> | ||
<math>u(t) = \frac{d\psi}{dt}</math> | : <math>u(t) = \frac{d\psi}{dt}</math> | ||
Jeśli do uzwojenia wtórnego dołączymy odbiornik, to pod wpływem napięcia indukowanego w tym uzwojeniu popłynie prąd <math>i_2(t)</math>. W zależności od środowiska w jakim zamyka się wytworzony wokół uzwojeń strumień magnetyczny rozróżniamy transformatory powietrzne (korpus transformatora wykonany z dielektryka o przenikalności magnetycznej względnej bliskiej jedności) i transformatory z rdzeniem ferromagnetycznym (korpus wykonany z rdzenia ferromagnetycznego). Zanim przejdziemy do omówienia obu rodzajów transformatorów, przedstawimy zależności obowiązujące dla transformatora idealnego. | Jeśli do uzwojenia wtórnego dołączymy odbiornik, to pod wpływem napięcia indukowanego w tym uzwojeniu popłynie prąd <math>i_2(t)</math>. W zależności od środowiska w jakim zamyka się wytworzony wokół uzwojeń strumień magnetyczny rozróżniamy transformatory powietrzne (korpus transformatora wykonany z dielektryka o przenikalności magnetycznej względnej bliskiej jedności) i transformatory z rdzeniem ferromagnetycznym (korpus wykonany z rdzenia ferromagnetycznego). Zanim przejdziemy do omówienia obu rodzajów transformatorów, przedstawimy zależności obowiązujące dla transformatora idealnego. | ||
| Linia 266: | Linia 261: | ||
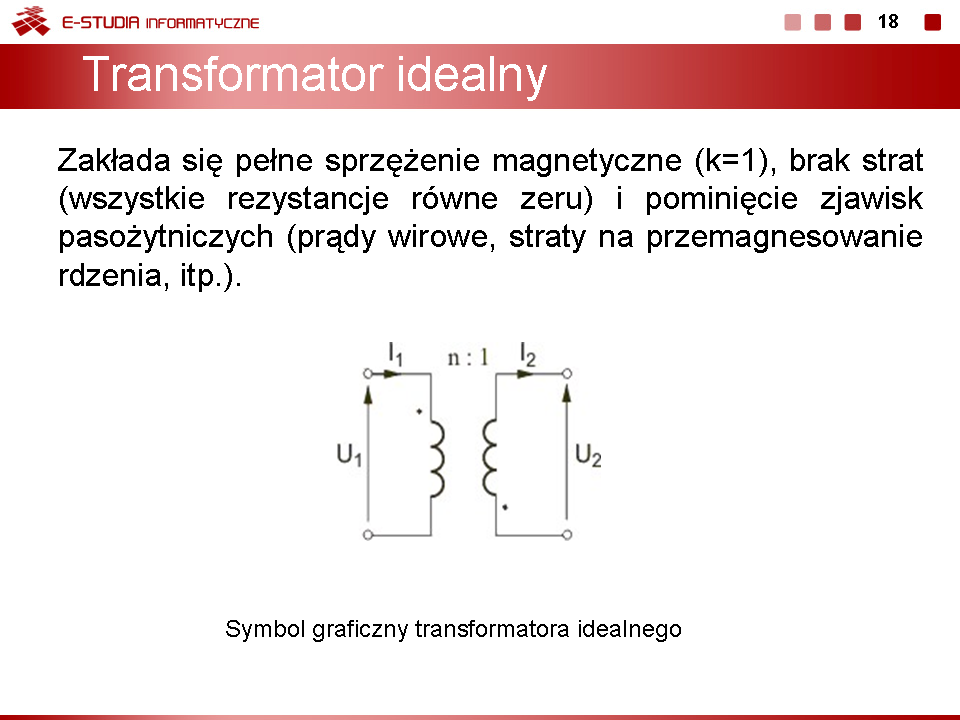
|valign="top"|Transformator idealny jest w pełni opisany poprzez tak zwaną '''przekładnię zwojową''', określającą stosunek napięcia pierwotnego do wtórnego ('''przekładnię napięciową''') na podstawie liczby zwojów pierwotnych i wtórnych. Przekładnia napięciowa transformatora idealnego niezależnie od sposobu wykonania i od obciążenia, powinna być równa przekładni zwojowej określonej wzorem | |valign="top"|Transformator idealny jest w pełni opisany poprzez tak zwaną '''przekładnię zwojową''', określającą stosunek napięcia pierwotnego do wtórnego ('''przekładnię napięciową''') na podstawie liczby zwojów pierwotnych i wtórnych. Przekładnia napięciowa transformatora idealnego niezależnie od sposobu wykonania i od obciążenia, powinna być równa przekładni zwojowej określonej wzorem | ||
<math>n=\frac{z_1}{z_2}</math> | : <math>n=\frac{z_1}{z_2}</math> | ||
Oznacza to, że relacja między napięciem pierwotnym i wtórnym jest następująca | Oznacza to, że relacja między napięciem pierwotnym i wtórnym jest następująca | ||
<math>\frac{U_1}{U_2}=n\rightarrow U_1=\frac{z_1}{z_2}U_2</math> | : <math>\frac{U_1}{U_2}=n\rightarrow U_1=\frac{z_1}{z_2}U_2</math> | ||
Wobec założenia o braku strat w samym transformatorze idealnym moc dostarczona na zaciski pierwotne równa się mocy na zaciskach wtórnych, to jest <math>S_1=S_2</math> (podobnie jest z mocą czynną i bierną). Przy oznaczeniu przekładni transformatora idealnego przez n, z warunku równości mocy wejściowej i wyjściowej, to znaczy <math>U_1I_1^*=U_2I_2^*</math> Wynika stąd relacja między prądem pierwotnym i wtórnym transformatora. Mianowicie | Wobec założenia o braku strat w samym transformatorze idealnym moc dostarczona na zaciski pierwotne równa się mocy na zaciskach wtórnych, to jest <math>S_1=S_2</math> (podobnie jest z mocą czynną i bierną). Przy oznaczeniu przekładni transformatora idealnego przez n, z warunku równości mocy wejściowej i wyjściowej, to znaczy <math>U_1I_1^*=U_2I_2^*</math> Wynika stąd relacja między prądem pierwotnym i wtórnym transformatora. Mianowicie | ||
<math>I_1=\frac{1}{n}I_2</math> | : <math>I_1=\frac{1}{n}I_2</math> | ||
Obie zależności można zapisać w następującej postaci macierzowej | Obie zależności można zapisać w następującej postaci macierzowej | ||
<math>\begin{bmatrix}U_1\\I_1\end{bmatrix}=\begin{bmatrix}n&0 \\0&\frac{1}{n}\end{bmatrix}\begin{bmatrix}U_2\\I_2\end{bmatrix}</math> | |||
: <math>\begin{bmatrix}U_1\\I_1\end{bmatrix}=\begin{bmatrix}n&0 \\0&\frac{1}{n}\end{bmatrix}\begin{bmatrix}U_2\\I_2\end{bmatrix}</math> | |||
Powyższe równanie macierzowe nazywane jest równaniem łańcuchowym transformatora idealnego. Wykonanie transformatora idealnego w praktyce nie jest możliwe, jednak współczesne realizacje techniczne transformatorów zwłaszcza transformatory z rdzeniem ferromagnetycznym są bliskie ideału. | Powyższe równanie macierzowe nazywane jest równaniem łańcuchowym transformatora idealnego. Wykonanie transformatora idealnego w praktyce nie jest możliwe, jednak współczesne realizacje techniczne transformatorów zwłaszcza transformatory z rdzeniem ferromagnetycznym są bliskie ideału. | ||
Wersja z 12:03, 31 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
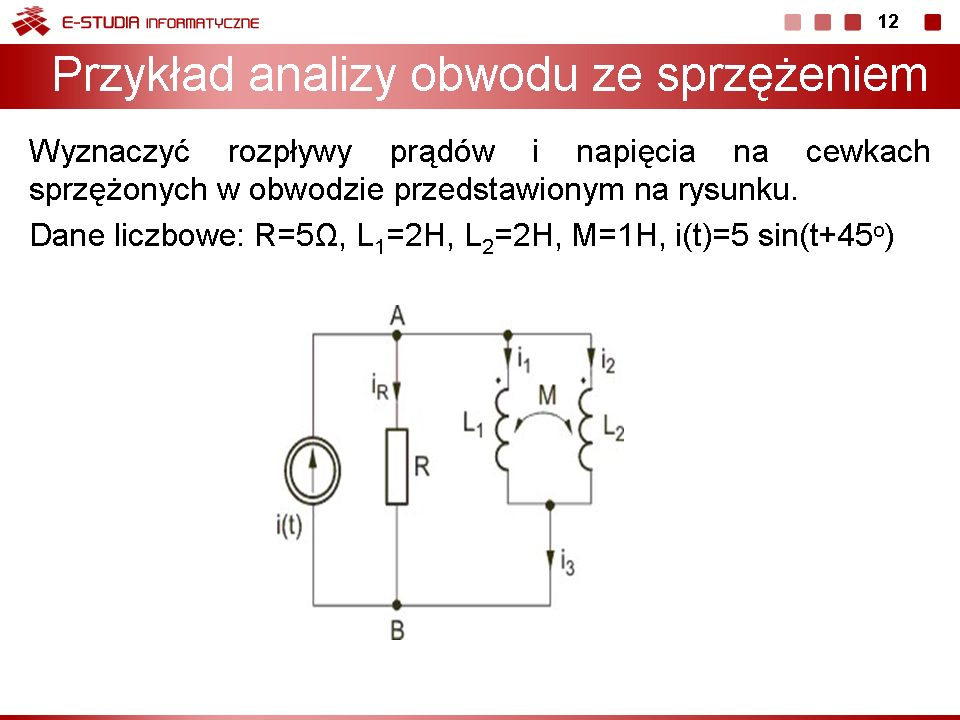
|
Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym.
Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. |

|
Rozwiązanie obwodu przebiega w następującej kolejności.
Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu:
|

|
Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej . Przyjmiemy następujące wartości parametrów obwodu: . |

|
Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami
|

|
Po wstawieniu wartości liczbowych otrzymuje się
|