PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 67: | Linia 67: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png]] | ||
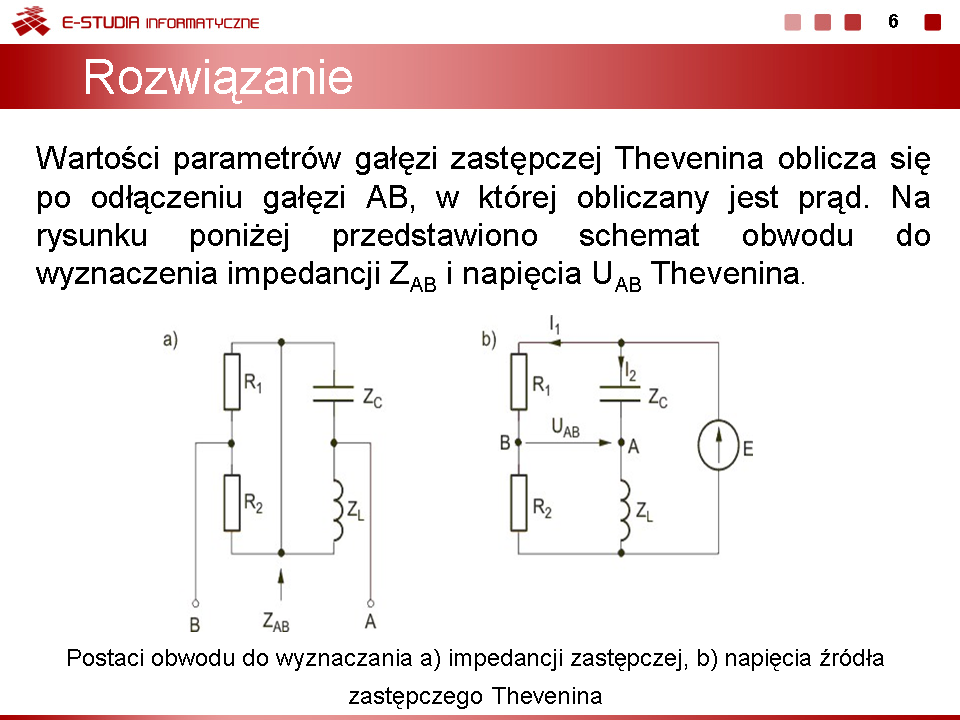
|valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | |valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | ||
: <math>Z_{AB}={R_1R_2 \over R_1+R_2}+{Z_LZ_C \over Z_L+Z_C}={5 \cdot 5 \over 5+5}+{j5 \cdot (-j10) \over j5-j10}=2,5+j10</math> | : <math>Z_{AB}={R_1R_2 \over R_1+R_2}+{Z_LZ_C \over Z_L+Z_C}={5 \cdot 5 \over 5+5}+{j5 \cdot (-j10) \over j5-j10}=2,5+j10</math> | ||
Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego <math>U_{AB}</math> w schemacie zastępczym Thevenina. Obliczając kolejno prądy | Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego <math>U_{AB}</math> w schemacie zastępczym Thevenina. Obliczając kolejno prądy | ||
: <math>I_1={E \over R_1+R_2}=1</math> | |||
: <math>I_2={E \over jX_L-jX_C}=2j</math> | : <math>I_2={E \over jX_L-jX_C}=2j</math> | ||
Napięcie <math>U_{AB}</math> określa się ze wzoru | Napięcie <math>U_{AB}</math> określa się ze wzoru | ||
: <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | : <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | ||
| Linia 90: | Linia 86: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png]] | ||
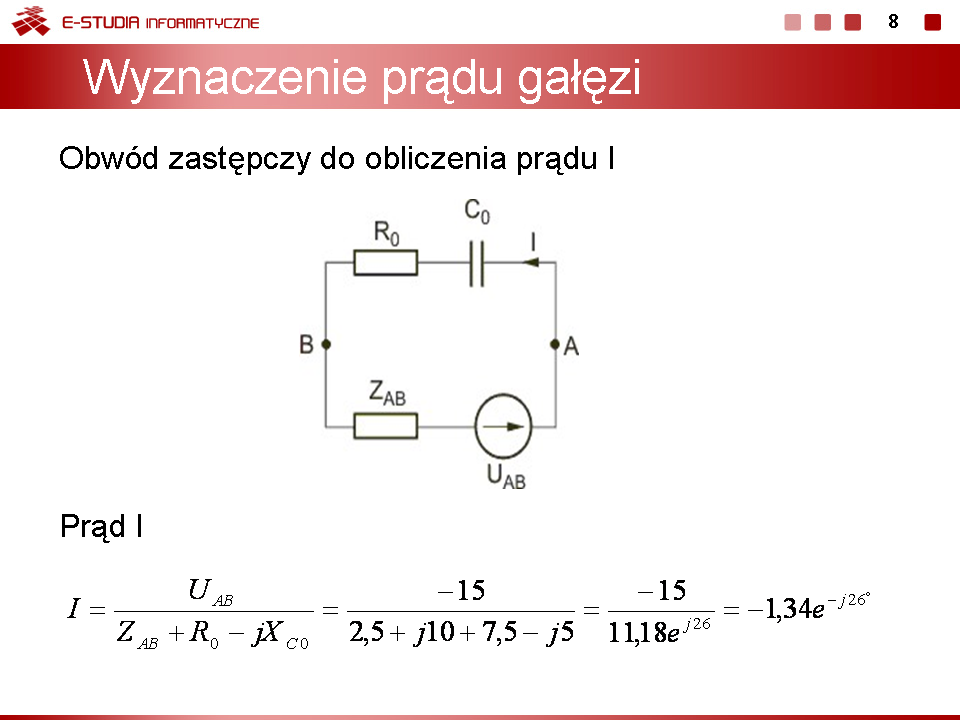
|valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\,</math> określa się ze wzoru | |valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\,</math> określa się ze wzoru | ||
: <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | : <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | ||
Wartości chwilowe prądu <math>i(t)\,</math> wyznaczane są z zależności | Wartości chwilowe prądu <math>i(t)\,</math> wyznaczane są z zależności | ||
: <math>i(t)=-1,34\sqrt{2}sin(\omega t-26^\circ)A</math> | : <math>i(t)=-1,34\sqrt{2}sin(\omega t-26^\circ)A</math> | ||
Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych. | Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych. | ||
| Linia 114: | Linia 106: | ||
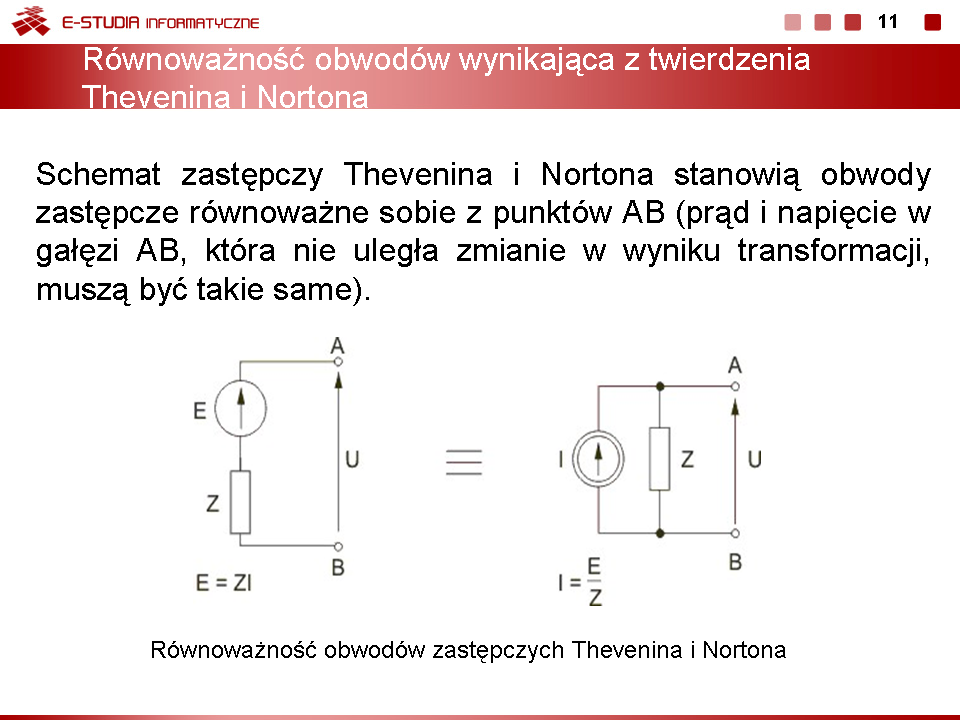
'''Twierdzenie Nortona''' | '''Twierdzenie Nortona''' | ||
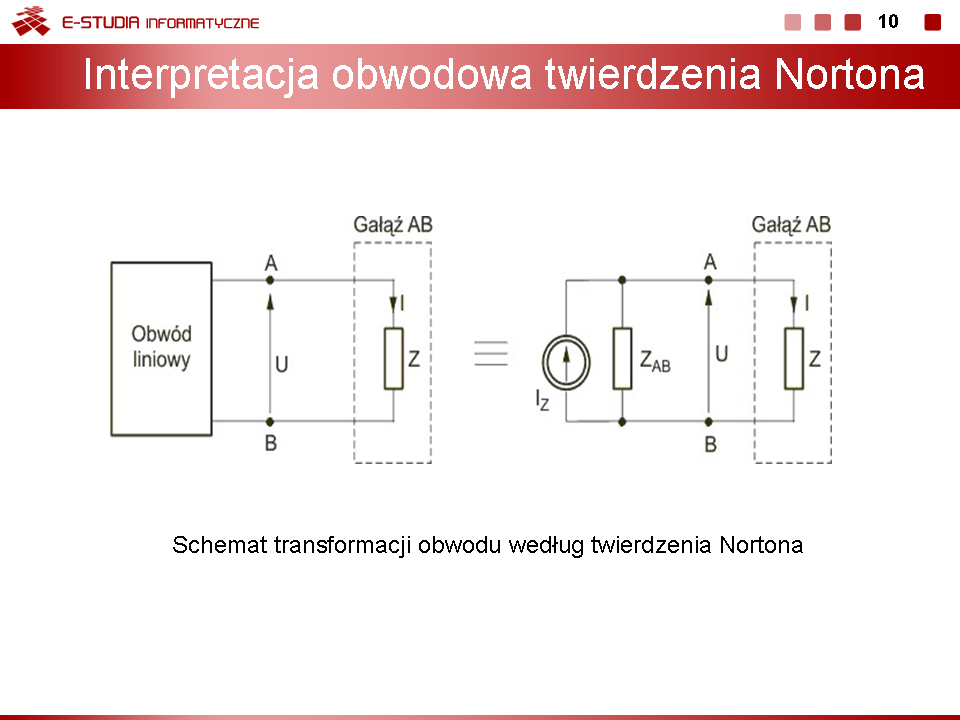
Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | ||
|} | |} | ||
| Linia 127: | Linia 117: | ||
Prąd <math>I\,</math> oraz napięcie <math>U\,</math> występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi <math>I\,</math> oraz napięciu <math>U\,</math> w tej samej gałęzi obwodu uproszczonego. Źródło prądowe <math>I_Z</math> występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja <math>Z_{AB}</math> jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB reprezentowana jest przez impedancję <math>Z\,</math>, napięcie tej gałęzi oblicza się z prawa prądowego Kirchhoffa <math>I_Z-U({1 \over Z}+{1 \over Z_{AB}})=0</math>, które pozwala wyrazić poszukiwane napięcie gałęzi w postaci | Prąd <math>I\,</math> oraz napięcie <math>U\,</math> występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi <math>I\,</math> oraz napięciu <math>U\,</math> w tej samej gałęzi obwodu uproszczonego. Źródło prądowe <math>I_Z</math> występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja <math>Z_{AB}</math> jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB reprezentowana jest przez impedancję <math>Z\,</math>, napięcie tej gałęzi oblicza się z prawa prądowego Kirchhoffa <math>I_Z-U({1 \over Z}+{1 \over Z_{AB}})=0</math>, które pozwala wyrazić poszukiwane napięcie gałęzi w postaci | ||
: <math>U={I_Z \over 1/Z+1/Z_{AB}}</math> | : <math>U={I_Z \over 1/Z+1/Z_{AB}}</math> | ||
Znajomość napięcia pozwala wyznaczyć na podstawie prawa Ohma prąd gałęzi korzystając z zależności <math>I=U/Z</math> Podobnie jak metoda Thevenina, zastosowanie twierdzenia Nortona umożliwia obliczenie prądu i napięcia tylko jednej gałęzi obwodu. Zwykle z punktu widzenia obliczeniowego wygodniejsze jest użycie metody Thevenina. | Znajomość napięcia pozwala wyznaczyć na podstawie prawa Ohma prąd gałęzi korzystając z zależności <math>I=U/Z</math> Podobnie jak metoda Thevenina, zastosowanie twierdzenia Nortona umożliwia obliczenie prądu i napięcia tylko jednej gałęzi obwodu. Zwykle z punktu widzenia obliczeniowego wygodniejsze jest użycie metody Thevenina. | ||
| Linia 175: | Linia 163: | ||
<math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | <math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | ||
w której <math>\mathbf{Y}</math>, jest macierzą węzłową o wymiarach <math>NxN\,</math>, gdzie <math>N\,</math> jest liczbą węzłów niezależnych w obwodzie, <math>\mathbf{V}\,</math> jest wektorem niezależnych potencjałów węzłowych o wymiarze <math>N\,</math> a <math>\mathbf{I}_{zr}</math> jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa <math>\mathbf{Y}</math>, określona jest w postaci | |||
<math>\mathbf{Y}=\begin{bmatrix} | <math>\mathbf{Y}=\begin{bmatrix} | ||
| Linia 187: | Linia 175: | ||
a wektory <math>\mathbf{V}</math>, oraz <math>\mathbf{I}_{zr}</math> dane są jak następuje | a wektory <math>\mathbf{V}</math>, oraz <math>\mathbf{I}_{zr}</math> dane są jak następuje | ||
<math>\mathbf{V}=\begin{bmatrix} | <math>\mathbf{V}=\begin{bmatrix} | ||
| Linia 227: | Linia 216: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd16.png]] | ||
|valign="top"|Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rysunku obok. | |valign="top"|Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rysunku obok. | ||
Korzystając z przedstawionych reguł formułowania równań węzłowych należy napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku. | Korzystając z przedstawionych reguł formułowania równań węzłowych należy napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku. | ||
| Linia 237: | Linia 225: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd17.png]] | ||
|valign="top"|Obwód zawiera 3 węzły niezależne: <math>V_1</math>, <math>V_2</math> oraz <math>V_3</math> mierzone względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez <math>Y_i\,</math>, gdzie <math>Y_i=1/Z_i</math> otrzymuje się macierz potencjałów węzłowych <math>\mathbf{Y}\,</math> oraz wektor prądów wymuszających <math>\mathbf{I}_{zr}</math> w postaci | |valign="top"|Obwód zawiera 3 węzły niezależne: <math>V_1</math>, <math>V_2</math> oraz <math>V_3</math> mierzone względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez <math>Y_i\,</math>, gdzie <math>Y_i=1/Z_i</math> otrzymuje się macierz potencjałów węzłowych <math>\mathbf{Y}\,</math> oraz wektor prądów wymuszających <math>\mathbf{I}_{zr}</math> w postaci | ||
<math>\begin{bmatrix} | <math>\begin{bmatrix} | ||
| Linia 255: | Linia 244: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
: <math>\mathbf{I}_{zr}= | : <math>\mathbf{I}_{zr}= | ||
| Linia 281: | Linia 271: | ||
: <math>I_2=Y_2(V_1-V_2)</math> | : <math>I_2=Y_2(V_1-V_2)</math> | ||
: <math>I_3=Y_3(V_2-E_3)</math> | : <math>I_3=Y_3(V_2-E_3)</math> | ||
: <math>I_4=Y_4(V_2-V_3)</math> | : <math>I_4=Y_4(V_2-V_3)</math> | ||
: <math>I_5=Y_5(V_3+E_5)</math> | : <math>I_5=Y_5(V_3+E_5)</math> | ||
: <math>I_6=Y_6V_3</math> | : <math>I_6=Y_6V_3</math> | ||
| Linia 305: | Linia 299: | ||
W metodzie prądów oczkowych, zwanej również metodą oczkową, wprowadza się prądy oczkowe jako zmienne, czyli prądy przypisane niezależnym oczkom występującym w obwodzie. Przykładowy wybór oczek niezależnych i oznaczenie prądów oczkowych obwodu przedstawiono na rysunku obok (slajd 20). | W metodzie prądów oczkowych, zwanej również metodą oczkową, wprowadza się prądy oczkowe jako zmienne, czyli prądy przypisane niezależnym oczkom występującym w obwodzie. Przykładowy wybór oczek niezależnych i oznaczenie prądów oczkowych obwodu przedstawiono na rysunku obok (slajd 20). | ||
|} | |} | ||
| Linia 313: | Linia 306: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd21.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd21.png]] | ||
|valign="top"|Oznaczmy w ogólności wektor prądów oczkowych w postaci | |valign="top"|Oznaczmy w ogólności wektor prądów oczkowych w postaci | ||
: <math>\mathbf{I}_o= | : <math>\mathbf{I}_o= | ||
| Linia 321: | Linia 315: | ||
I_{oN} | I_{oN} | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
w której <math>I_{ok}</math> oznacza prąd oczkowy <math>k\,</math>-tego oczka. Dla uzyskania opisu oczkowego wykorzystuje się prawo napięciowe Kirchhoffa napisane dla wszystkich oczek niezależnych obwodu. Następnie wyraża się wszystkie prądy gałęziowe poprzez prądy oczkowe (prąd gałęziowy jest równy sumie lub różnicy prądów oczkowych przeprowadzonych przez daną gałąź) i otrzymuje opis obwodu w postaci układu równań oczkowych | w której <math>I_{ok}</math> oznacza prąd oczkowy <math>k\,</math>-tego oczka. Dla uzyskania opisu oczkowego wykorzystuje się prawo napięciowe Kirchhoffa napisane dla wszystkich oczek niezależnych obwodu. Następnie wyraża się wszystkie prądy gałęziowe poprzez prądy oczkowe (prąd gałęziowy jest równy sumie lub różnicy prądów oczkowych przeprowadzonych przez daną gałąź) i otrzymuje opis obwodu w postaci układu równań oczkowych | ||
| Linia 326: | Linia 321: | ||
: <math>\mathbf{ZI}_o=\mathbf{E}</math> | : <math>\mathbf{ZI}_o=\mathbf{E}</math> | ||
gdzie macierz oczkowa <math>\mathbf{Z}\,</math> oraz wektor napięć wymuszających <math>\mathbf{E}\,</math> przyjmują postać | |||
: <math>\mathbf{Z}= | : <math>\mathbf{Z}= | ||
| Linia 336: | Linia 331: | ||
Z_{N1} & Z_{N2} & \cdots & Z_{NN} | Z_{N1} & Z_{N2} & \cdots & Z_{NN} | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
: <math>\mathbf{E}= | : <math>\mathbf{E}= | ||
| Linia 403: | Linia 399: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd26.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd26.png]] | ||
|valign="top"|Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie | |valign="top"|Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie | ||
: <math>I_1=I_{03}-I_{01}</math> | : <math>I_1=I_{03}-I_{01}</math> | ||
| Linia 416: | Linia 411: | ||
: <math>I_6=-I_{03}</math> | : <math>I_6=-I_{03}</math> | ||
|} | |} | ||
| Linia 444: | Linia 437: | ||
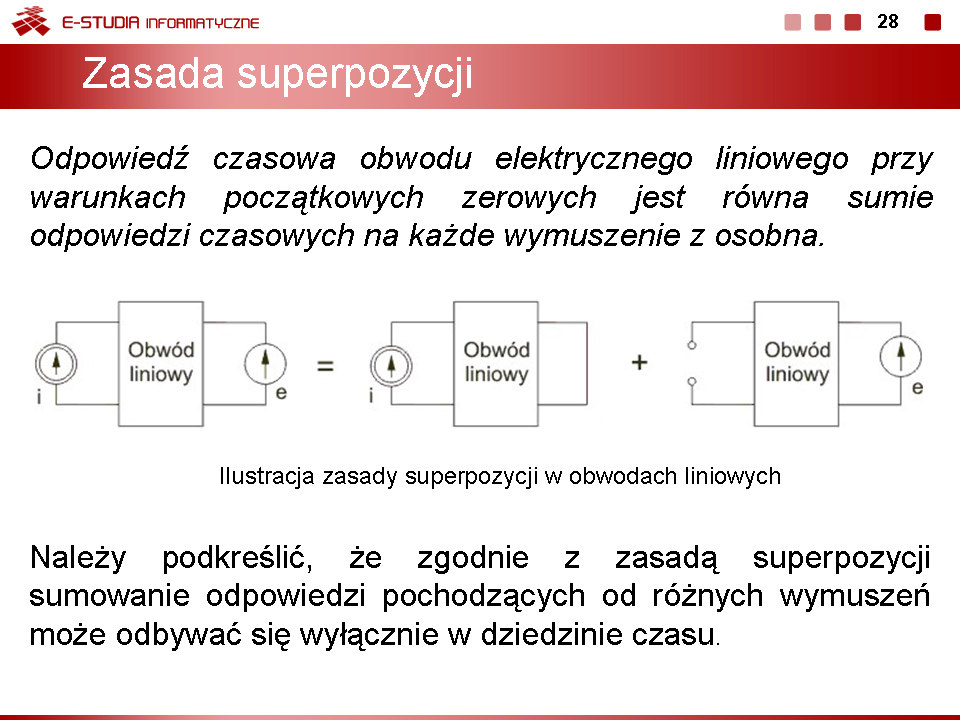
Należy podkreślić, że zgodnie z zasadą superpozycji sumowanie odpowiedzi pochodzących od różnych wymuszeń może odbywać się wyłącznie w dziedzinie czasu. Sumowanie wartości zespolonych od poszczególnych wymuszeń byłoby poważnym błędem, gdyż sugerowałoby istnienie rozwiązania obwodu zawierającego tylko jedną harmoniczną. Ilustrację stosowania zasady superpozycji w analizie obwodów przedstawiono na rysunku obok (slajd 28). | Należy podkreślić, że zgodnie z zasadą superpozycji sumowanie odpowiedzi pochodzących od różnych wymuszeń może odbywać się wyłącznie w dziedzinie czasu. Sumowanie wartości zespolonych od poszczególnych wymuszeń byłoby poważnym błędem, gdyż sugerowałoby istnienie rozwiązania obwodu zawierającego tylko jedną harmoniczną. Ilustrację stosowania zasady superpozycji w analizie obwodów przedstawiono na rysunku obok (slajd 28). | ||
|} | |} | ||
| Linia 466: | Linia 458: | ||
[[Grafika:PEE_M4_zadanie_4_1_a.png]] | [[Grafika:PEE_M4_zadanie_4_1_a.png]] | ||
<math>Z_{AB}={R_1R_3 \over R_1+R_3}+{R_2R_4 \over R_2+R_4}=2,93</math> | : <math>Z_{AB}={R_1R_3 \over R_1+R_3}+{R_2R_4 \over R_2+R_4}=2,93</math> | ||
Prądy w obwodzie z rys. b: | Prądy w obwodzie z rys. b: | ||
<math>I_1={E \over R_1+R_3}={30 \over 6}=5</math> | : <math>I_1={E \over R_1+R_3}={30 \over 6}=5</math> | ||
<math>I_2={E \over R_2+R_4}={30 \over 10}=3</math> | : <math>I_2={E \over R_2+R_4}={30 \over 10}=3</math> | ||
Napięcie <math>U_{AB}</math> | Napięcie <math>U_{AB}</math> | ||
<math>U_{AB}=R_2I_2-R_1I_1=4</math> | : <math>U_{AB}=R_2I_2-R_1I_1=4</math> | ||
Poszukiwany prąd <math>I_x</math> z obwodu zastępczego Thevenina (rys. c) | Poszukiwany prąd <math>I_x</math> z obwodu zastępczego Thevenina (rys. c) | ||
<math>I_x={U_{AB} \over Z_{AB}}=1,36A</math> | : <math>I_x={U_{AB} \over Z_{AB}}=1,36A</math> | ||
| Linia 497: | Linia 489: | ||
Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci | Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci | ||
<math> | |||
: <math> | |||
\begin{bmatrix} | \begin{bmatrix} | ||
Y_1+Y_2 & -Y_2 & 0\\ | Y_1+Y_2 & -Y_2 & 0\\ | ||
| Linia 527: | Linia 520: | ||
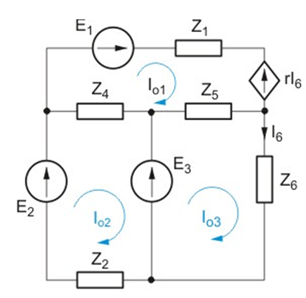
Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci | Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci | ||
: <math> | : <math> | ||
Wersja z 11:54, 31 sie 2006

|
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |

|
Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie
|
| Zadania sprawdzające
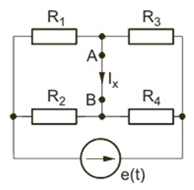
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , .
Impedancja z zacisków AB obwodu (rysunek a) jest równa
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci
|