PKow: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
| Linia 5: | Linia 5: | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Ciag dalszy</span> | |||
<div class="exercise"> | |||
Spróbuj obniżyć koszt wyznaczania <math>\displaystyle \exp(x)</math> dla dużych <math>\displaystyle x</math>! | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | |||
<div style="font-size:smaller; background-color:#efe"> Rzecz w tym, że dla dużych <math>\displaystyle x</math>, trzeba wziąć bardzo dużo wyrazów w szeregu | |||
Taylora. Czy można tak wykombinować, by w rezultacie wziąć ich mniej? </div> | |||
</div></div> | |||
</div></div> | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | ||
[ | Bez zmieniejszenia ogólności, załóżmy, że <math>\displaystyle x\geq 0</math>. | ||
Jeśli <math>\displaystyle x = k + t</math>, gdzie <math>\displaystyle t \in [0,1)</math>, a <math>\displaystyle k</math> jest całkowite, to oczywiście | |||
<center><math>\displaystyle | |||
e^x = e^{k+t} = e^k e^t = e^k \exp(t). | |||
</math></center> | |||
</ | Tak więc zadanie redukuje się do wyznaczenia <math>\displaystyle \exp(t)</math> dla ''małego'' <math>\displaystyle t</math> oraz | ||
do co najwyżej <math>\displaystyle k</math> dodatkowych mnożeń potrzebnych do wyznaczenia całkowitej | |||
potęgi <math>\displaystyle e^k</math> (ile mnożeń ''naprawdę'' wystarczy?). Pamiętaj, przyjęliśmy, że | |||
znamy reprezentację numeryczną liczby <math>\displaystyle e</math>. | |||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
[Wersja B] | |||
function [y, N] <nowiki>=</nowiki> expb(x, epsilon) | |||
k <nowiki>=</nowiki> floor(x); t <nowiki>=</nowiki> x - k; | |||
[y, N] <nowiki>=</nowiki> expa(t, epsilon); | |||
for i <nowiki>=</nowiki> 1:k | |||
y *<nowiki>=</nowiki> e; | |||
end | |||
N +<nowiki>=</nowiki> (k+2); | |||
end | |||
</pre></div> | |||
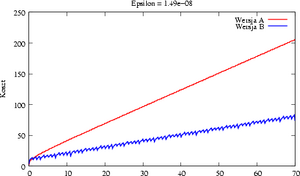
[[Image:MNkosztexpab.png|thumb|300px|Wersja B, w której sprytnie redukujemy zadanie do | |||
wyznaczania <math>\displaystyle e^t</math> dla <math>\displaystyle t\in [0,1]</math> jest istotnie tańsza.]] | |||
</div></div></div> | |||
Wersja z 14:02, 29 sie 2006
Wyznaczanie wektorów i wartości własnych
Przykład Moj przykład
Tekst
Algorytm Nie robiący nic
Leż
Ćwiczenie: Ciag dalszy
Spróbuj obniżyć koszt wyznaczania dla dużych !
Wskazówka
Rozwiązanie