|
|
| Linia 4: |
Linia 4: |
| {{algorytm|Nie robiący nic||Leż}} | | {{algorytm|Nie robiący nic||Leż}} |
|
| |
|
| Niech będzie dana rzeczywista kwadratowa macierz <math>\displaystyle A</math> wymiaru <math>\displaystyle N</math>. Wektorem własnym <math>\displaystyle x\in C^N</math> oraz
| |
| odpowiadającą mu wartością własną <math>\displaystyle \lambda \in C</math> nazwiemy taką parę, dla której
| |
|
| |
|
| <center><math>\displaystyle A x = \lambda x,
| |
| </math></center>
| |
|
| |
|
| przy czym <math>\displaystyle x\neq 0</math>.
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> |
| | W pierwszym odruchu myślimy o szeregu definiującym funkcję wykładniczą, |
|
| |
|
| Zadanie wyznaczania wartości własnych i wektorów własnych macierzy ma bardzo
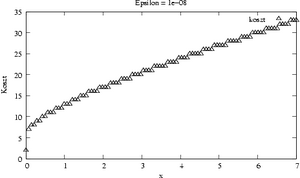
| | [[Image:MNkosztexpa.png|thumb|300px|Koszt aproksymacji wielomianem Taylora.]] |
| szerokie zastosowania w tak odległych do siebie dziedzinach jak np. analiza
| |
| odporności konstrukcji mechanicznych (wieżowce, mosty, wagony kolejowe) na
| |
| wibracje, czy też rankingowanie stron internetowych w wyszukiwarce Google.
| |
|
| |
|
| {{przyklad|Odporność budynku na trzęsienie ziemi||
| | </div></div></div> |
|
| |
|
| Rozważmy prosty układ mechaniczny opisujący, naturalnie w pewnym
| | nie pokazuje obrazka, chociaż gdy na tej samej stronie umiescic go bez ukrywajki |
| jedynie przybliżeniu, zachowanie się układu <math>\displaystyle N</math> ciężkich płyt połączonych ze
| |
| sobą relatywnie elatycznymi dźwigarami --- co może np. modelować konstrukcję
| |
| wieżowca.
| |
|
| |
|
| {}{Model wieżowca poddanego drganiom poprzecznym}
| | [[Image:MNkosztexpa.png|thumb|300px|Koszt aproksymacji wielomianem Taylora.]] |
| | |
| Wiadomo, że jeśli częstotliwości drgań własnych tego wieżowca będą bliskie
| |
| częstotliwości siły wymuszającej (o niewielkiej amplitudzie), to konstrukcja
| |
| wpadnie w rezonans i w końcu rozpadnie się wskutek zbyt wielkich przemieszczeń.
| |
| Wychylenia naszych płyt z położenia równowagi są opisywane układem pewnych
| |
| równań różniczkowych.
| |
| Teoria matematyczna takich równań różniczkowych pokazuje, że częstotliwości
| |
| drgań własnych to nic innego jak ''wartości własne'' pewnej
| |
| {niesymetrycznej} macierzy
| |
| wymiaru <math>\displaystyle 2N</math>,
| |
| która powstaje ze współczynników równania różniczkowego opisującego dynamikę
| |
| tego układu.
| |
| }}
| |
| | |
| {{przyklad|Macierz Google'a||
| |
| | |
| Podstawowy algorytm rankingowania stron WWW w {http://www.wikipedia.org/pagerank}{wyszukiwarce Google}
| |
| sprowadza się do znalezienia rzeczywistego ''wektora własnego'' <math>\displaystyle \pi</math> pewnej silnie
| |
| rozrzedzonej macierzy <math>\displaystyle A</math> (gigantycznego rozmiaru, równego liczbie indeksowanych
| |
| stron, czyli w chwili pisania tego tekstu około {ilu} stron), odpowiadającego wartości własnej równej 1:
| |
| | |
| <center><math>\displaystyle A \pi = \pi.
| |
| </math></center>
| |
| | |
| Współrzędne wektora <math>\displaystyle \pi</math>
| |
| interpretuje się jako wartość rankingową kolejnych stron WWW. Aby wszystko miało
| |
| sens, współrzędne wektora muszą być z przedziału [0,1]. Pewne
| |
| twierdzenia matematyczne i subtelny dobór macierzy <math>\displaystyle A</math> gwarantują, że taki
| |
| wektor <math>\displaystyle \pi</math> zawsze istnieje i jest jedyny! Co więcej, wartość 1 jest
| |
| dominującą wartością własną <math>\displaystyle A</math>, a to z kolei ma ważne znaczenie dla tzw.
| |
| {sec:metoda-potegowa}{metody potęgowej} numerycznego wyznaczania takiego wektora.
| |
| }}
| |
| | |
| {{przyklad|Wyznaczanie miejsc zerowych wielomianu||
| |
| | |
| Jak wiadomo, wartości własne to miejsca zerowe wielomianu charakterystycznego
| |
| macierzy <math>\displaystyle P(\lambda) = \det(A - \lambda I)</math>. Zachodzi także fakt odwrotny, to
| |
| znaczy miejsca zerowe wielomianu są wartościami pewnej macierzy, np. miejsca
| |
| zerowe wielomianu
| |
| | |
| <center><math>\displaystyle p(\lambda) = p_1 \lambda^N + \ldots + p_N \lambda + p_{N+1}
| |
| </math></center>
| |
| | |
| są wartościami własnymi m.in. macierzy stowarzyszonej,
| |
| | |
| <center><math>\displaystyle A = \beginpmatrix
| |
| -p_2/p_1 & -p_3/p_1 & \cdots & -p_{N+1}/p_1\\
| |
| 1 & & & \\
| |
| & 1 & & \\
| |
| & & \ddots & \\
| |
| & & & 1
| |
| \endpmatrix
| |
| </math></center>
| |
| | |
| Funkcja Octave'a !compan(p)! wyznacza macierz stowarzyszoną dla zadanego
| |
| wielomianu o współczynnikach w wektorze <math>\displaystyle p = [p_1,\ldots,p_N, p_{N+1}]^T</math>. Z tej
| |
| macierzy korzysta następnie funkcja Octave'a !roots!, która właśnie w taki
| |
| sposób wyznacza pierwiastki wielomianów: jako wartości własne macierzy
| |
| stowarzyszonej.
| |
| }}
| |
| | |
| {{przyklad|||
| |
| Praktyczne zadanie z macierzą symetryczną
| |
| }}
| |
| | |
| W praktyce obliczeniowej spotyka się zazwyczaj kilka typów zagadnień:
| |
| * Wyznaczenie dominującej wartości własnej (to znaczy: największej co do
| |
| modułu) i odpowiadającego jej wektora własnego (a może kilku wektorów?)
| |
| * Wyznaczenie najmniejszej co do modułu wartości własnej i wektorów jej
| |
| odpowiadających (zauważmy, że to jest np. zadanie wyznaczenia ''jądra
| |
| macierzy osobliwej'' --- wtedy wiemy a priori, że szukana najmniejsza co do modułu
| |
| wartość własna to zero)
| |
| * Wyznaczenie wartości własnej najbliższej zadanej liczbie (to jest właśnie
| |
| odpowiedź na pytanie jak blisko częstości wymuszającej są częstości drgań
| |
| własnych budynku)
| |
| * Wyznaczenie wszystkich wartości własnych (na przykład, w celu znalezienia
| |
| wszystkich pierwiastków zadanego wielomianu)
| |
| * Wyznaczenie wszystkich wartości i wektorów własnych (tzw. pełne
| |
| zagadnienie własne)
| |
| | |
| Jak domyślamy się, dla macierzy rozrzedzonych dużego wymiaru pełne zagadnienie
| |
| własne jest zbyt kosztowne, gdyż najczęściej macierz wektorów własnych --- nawet
| |
| dla macierzy rzadkiej --- jest gęsta.
| |
| | |
| Ponieważ w zastosowaniach bardzo często pojawiają się macierze rzeczywiste
| |
| symetryczne (powyższe przykłady pokazują, że nie tylko!) szczegółową analizę
| |
| metod numerycznych ograniczymy do tego przypadku, gdyż wtedy zachodzi
| |
| | |
| {{twierdzenie|o symetrycznym zadaniu włanym||
| |
| | |
| Każda macierz rzeczywista symetryczna <math>\displaystyle A</math> wymiaru <math>\displaystyle N</math> ma rozkład
| |
| | |
| <center><math>\displaystyle A = Q\Lambda Q^T,
| |
| </math></center>
| |
| | |
| gdzie <math>\displaystyle Q\in R^{N\times N}</math> jest ortogonalna (tzn. <math>\displaystyle Q^TQ = I</math>), a jej kolumnami są
| |
| wektory własne <math>\displaystyle A</math>, natomiast <math>\displaystyle \Lambda\in
| |
| R^N</math> jest diagonalna z
| |
| wartościami własnymi <math>\displaystyle A</math> na diagonali:
| |
| | |
| <center><math>\displaystyle \Lambda = \beginpmatrix \lambda_1 & & \\ & \ddots & \\ & &
| |
| \lambda_N\endpmatrix .
| |
| </math></center>
| |
| | |
| }}
| |
| | |
| ===Uwarunkowanie zadania===
| |
| | |
| {{twierdzenie|Bauer-Fike||
| |
| | |
| Niech <math>\displaystyle A\in R^{N\times N}</math> będzie diagonalizowalna, to
| |
| znaczy dla pewnej macierzy <math>\displaystyle X</math> zachodzi
| |
| | |
| <center><math>\displaystyle X^{-1} A X = \beginpmatrix \lambda_1 & & \\ & \ddots & \\ & &
| |
| \lambda_N\endpmatrix ,
| |
| </math></center>
| |
| | |
| a więc (gdyż macierz po prawej stronie jest podobna do <math>\displaystyle A</math>) <math>\displaystyle \lambda_i\in C</math>,
| |
| <math>\displaystyle i=1,\ldots,N</math> są
| |
| wartościami własnymi <math>\displaystyle A</math>. Rozważmy macierz zaburzoną <math>\displaystyle \tilde{A}</math> i jakąś jej
| |
| wartość własną <math>\displaystyle \tilde{\lambda}</math>. Wtedy istnieje wartość własna <math>\displaystyle \lambda_j</math>
| |
| macierzy <math>\displaystyle A</math> taka, że
| |
| | |
| <center><math>\displaystyle |\lambda_j - \tilde{\lambda}| \leq </math> cond <math>\displaystyle _2(X) ||A - \tilde{A}||_2.
| |
| </math></center>
| |
| | |
| }}
| |
| | |
| Ponieważ dla rzeczywistej macierzy symetrycznej macierz przejścia <math>\displaystyle X</math> jest
| |
| ortogonalna,
| |
| <math>\displaystyle X^{-1} = X^T</math>, to mamy cond <math>\displaystyle _2(X) = 1</math> i w konsekwencji zachodzi
| |
| | |
| {{wniosek|Wartości własne macierzy symetrycznej są doskonale uwarunkowane||
| |
| | |
| Przy oznaczeniach jak {thm:Bauer-Fike}{twierdzeniu Bauera-Fike'a}, jeśli
| |
| dodatkowo założymy, że macierz <math>\displaystyle A</math> jest rzeczywista i symetryczna, to
| |
| | |
| <center><math>\displaystyle \min_{j=1,\ldots,N}|\lambda_j - \tilde{\lambda}| \leq ||A - \tilde{A}||_2.
| |
| </math></center>
| |
| | |
| }}
| |
| | |
| Z drugiej strony, dla macierzy niediagonalizowalnych, uwarunkowanie wartości
| |
| własnych może być
| |
| dowolnie duże, co ilustruje poniższy
| |
| | |
| {{przyklad|||
| |
| | |
| <center><math>\displaystyle A_\epsilon = \beginpmatrix a & 1 \\ \epsilon & a \endpmatrix
| |
| </math></center>
| |
| | |
| Weźmy dla uproszczenia <math>\displaystyle a=0</math>.
| |
| Wartości własne <math>\displaystyle A_\epsilon</math> to zera wielomianu <math>\displaystyle p_\epsilon(\lambda) = \lambda^2 - \epsilon</math>,
| |
| zatem <math>\displaystyle \lambda_\epsilon = \pm \sqrt{\epsilon}</math> i w konsekwencji
| |
| | |
| <center><math>\displaystyle |\lambda_\epsilon - \lambda_0| / ||A_\epsilon - A_0|| = \sqrt{\epsilon}/\epsilon
| |
| \rightarrow \infty,
| |
| </math></center>
| |
| | |
| gdy <math>\displaystyle \epsilon \rightarrow 0^+</math>, a więc uwarunkowanie takiego zadania jest
| |
| nieskończone: dowolnie mała zmiana macierzy powoduje zaburzenie wartości
| |
| własnych niewspółmiernie wielkie wobec zaburzenia danych. Dodatkowo, wartości własne i wektory własne macierzy <math>\displaystyle A</math> dla
| |
| ujemnego parametru <math>\displaystyle \epsilon</math> są zespolone!
| |
| | |
| {eigencond.png}{Zachowanie się wartości własnych macierzy <math>\displaystyle A</math> (z
| |
| parametrem <math>\displaystyle a=1</math>) w otoczeniu <math>\displaystyle \delta = 0</math>}
| |
| | |
| }}
| |
| | |
| Bardziej spektakularny przykład pochodzi od Wilkinsona:
| |
| | |
| {{przyklad|Perfidny wielomian Wilkinsona||
| |
| | |
| Niech
| |
| | |
| <center><math>\displaystyle p(\lambda) = (\lambda -1)(\lambda - 2) \cdots (\lambda - 20).
| |
| </math></center>
| |
| | |
| Zmiana współczynnika przy <math>\displaystyle \lambda^{19}</math> o <math>\displaystyle 10^{-7}</math> skutkuje presunięciem niektórych
| |
| miejsc zerowych nawet o kilka jednostek na płaszczyźnie zespolonej! Poniżej
| |
| pokazujemy to na numerycznym przykładzie, gdzie prócz w/w zaburzenia mamy
| |
| dodatkowo z zaburzeniami powstałymi wskutek wyznaczenia współczynników
| |
| wielomianu w arytmetyce zmiennoprzecinkowej.
| |
| | |
| {wilkinson.png}{Zera oryginalnego i lekko zaburzonego perfidnego wielomianu
| |
| Wilkinsona.}
| |
| | |
| Jak widzimy, zera bardzo mało zaburzonego wielomianu mogą stać się wyraźnie nie-rzeczywiste!
| |
| | |
| }}
| |
| | |
| Jeśli chodzi o wektory własne, ich wrażliwość na zaburzenia macierzy jest
| |
| bardziej skomplikowana i zależy m.in. od uwarunkowania wartości własnych (czego
| |
| łatwo się domyślić) oraz od tego, jak blisko siebie leżą wartości własne.
| |
| | |
| ===Lokalizacja wartości własnych===
| |
| | |
| Jak okaże się za chwilę, czasem warto mieć ogólne rozeznanie o tym, gdzie ''z
| |
| grubsza'' leżą wartości własne danej macierzy <math>\displaystyle A</math>. W tym celu mogą być nam
| |
| pomocne dwa fakty:
| |
| | |
| {{fakt|||
| |
| Dowolna wartość własna <math>\displaystyle \lambda\in C</math> macierzy <math>\displaystyle A</math> spełnia
| |
| | |
| <center><math>\displaystyle |\lambda| \leq ||A||,
| |
| </math></center>
| |
| | |
| gdzie <math>\displaystyle ||A||</math> jest dowolną normą macierzową indukowaną przez normę wektorową.
| |
| }}
| |
| | |
| Rzeczywiście, skoro istnieje wektor <math>\displaystyle x\neq 0</math> taki, że <math>\displaystyle Ax = \lambda x</math>, to stąd
| |
| <math>\displaystyle ||Ax||/||x|| = |\lambda|</math>, więc fakt powyższy wynika już z definicji normy
| |
| macierzy:
| |
| | |
| <center><math>\displaystyle ||A|| = \max_{y\neq 0}\frac{||Ay||}{||y||} \geq ||Ax||/||x||.
| |
| </math></center>
| |
| | |
| Drugie twierdzenie jest równie proste w dowodzie, ale daje trochę więcej
| |
| informacji o lokalizacji widma.
| |
| | |
| {{twierdzenie|Gerszgorina||
| |
| | |
| Wartości własne macierzy <math>\displaystyle A</math> leżą w sumie (teoriomnogościowej) dysków <math>\displaystyle K_i</math> na
| |
| płaszczyźnie zespolonej,
| |
| | |
| <center><math>\displaystyle K_i = \{z \in C: |z - a_{ii}| \leq \sum_{j\neq i} |a_{ij}| \}, \qquad i =
| |
| 1,\ldots N.
| |
| </math></center>
| |
| | |
| }}
| |
| | |
| {{przyklad|Koła Gerszgorina||
| |
| | |
| Niech
| |
| | |
| <center><math>\displaystyle A = \beginpmatrix
| |
| 1.08930 & 1.38209 & -1.00037 & 0.69355 & 2.32178 \\
| |
| 0.14211 & 1.74696 & 1.68440 & 0.30664 & 1.26718 \\
| |
| -0.74620 & 2.02686 & -0.68293 & 0.19684 & 0.35854 \\
| |
| 0.83517 & 0.74987 & 1.71331 & 1.09765 & -0.44321 \\
| |
| 1.02132 & -2.62155 & 0.79247 & 1.11408 & 0.48076 \\
| |
| \endpmatrix
| |
| </math></center>
| |
| | |
| {gershgorindisks.png}{Lokalizacja wartości własnych macierzy <math>\displaystyle A</math> kołami Gerszgorina oraz zgrubna
| |
| lokalizacja wewnątrz okręgu
| |
| o promieniu równym <math>\displaystyle ||A||_1</math>. Dokładne wartości własne zaznaczone trójkącikami.}
| |
| | |
| }}
| |
| | |
| {{przyklad|Widmo macierzy jednowymiarowego Laplasjanu||
| |
| | |
| Norma daje:
| |
| | |
| Tw. Gerszgorina daje:
| |
| | |
| W rzeczywistości,
| |
| | |
| }}
| |
| | |
| ===Metoda potęgowa, odwrotna potęgowa, RQI===
| |
| | |
| ====Metoda potęgowa====
| |
| | |
| Przypuśćmy, że wartości własne macierzy <math>\displaystyle A\in R^{N\times N}</math> spełniają
| |
| | |
| <center><math>\displaystyle |\lambda_1| > |\lambda_2| \geq \ldots \geq |\lambda_N|,
| |
| </math></center>
| |
| | |
| (to znaczy, istnieje dokładnie jedna ''dominująca'' wartość własna macierzy
| |
| <math>\displaystyle A</math>.
| |
| | |
| Załóżmy także, że istnieje baza złożona z wektorów własnych <math>\displaystyle q_1,\ldots,q_N</math> tej
| |
| macierzy (tak jest np. dla macierzy symetrycznej na mocy
| |
| {thm:symetric-eig}{twierdzenia o własnościach symetrycznego zadania
| |
| własnego}).
| |
| | |
| Kierunek własny <math>\displaystyle q_k</math> jakiejś macierzy <math>\displaystyle A</math> ma taką własność, że poddany działaniu przekształcenia
| |
| <math>\displaystyle A</math> wydłuża się <math>\displaystyle \lambda_k</math> razy, wobec tego, dowolny wektor <math>\displaystyle x\in R^N</math> poddany
| |
| działaniu <math>\displaystyle A</math> najbardziej wydłuży się w kierunku <math>\displaystyle q_1</math>. Iterując tę procedurę,
| |
| powinniśmy dostawać w wyniku wektory, w których coraz bardziej dominuje kierunek
| |
| <math>\displaystyle q_1</math>. Formalnie, niech
| |
| | |
| <center><math>\displaystyle x = \alpha_1q_1 + \ldots + \alpha_Nq_N,
| |
| </math></center>
| |
| | |
| wtedy
| |
| | |
| <center><math>\displaystyle Ax = A \left( \sum_i \alpha_iq_i \right) = \sum_i \alpha_i A q_i
| |
| = \sum_i \alpha_i \lambda_i q_i
| |
| </math></center>
| |
| | |
| i w konsekwencji
| |
| | |
| <center><math>\displaystyle A^kx = \sum_i \alpha_i \lambda_i^k q_i = \lambda_1^k\left(\alpha_1q_1 +
| |
| \alpha_2\left(\frac{\lambda_2}{\lambda_1}\right)^kq_2 + \ldots +
| |
| \alpha_N\left(\frac{\lambda_N}{\lambda_1}\right)^kq_N \right).
| |
| </math></center>
| |
| | |
| Ponieważ z założenia, że istnieje dokładnie jedna dominująca wartość własna,
| |
| <math>\displaystyle \left|\frac{\lambda_N}{\lambda_1}\right| < 1</math>, to wyrażenie w nawiasie dąży do
| |
| <math>\displaystyle \alpha_1q_1</math> i w konsekwencji wektory <math>\displaystyle x_k = A^kx</math> dążą, gdy
| |
| <math>\displaystyle k\rightarrow\infty</math>, do kierunku wektora własnego <math>\displaystyle q_1</math>, to znaczy wektora
| |
| odpowiadającego dominującej wartości własnej <math>\displaystyle A</math> (o ile tylko <math>\displaystyle \alpha_1
| |
| \neq 0</math>).
| |
| | |
| Szybkość zbieżności metody potęgowej jest liniowa, o współczynniku zależnym od
| |
| stosunku <math>\displaystyle \lambda_2/\lambda_1|</math>. W patologicznym przypadku, gdy <math>\displaystyle |\lambda_1|
| |
| \approx |\lambda_2|</math>, może więc okazać się, że metoda praktycznie nie jest
| |
| zbieżna.
| |
| | |
| W praktyce nie wyznaczamy wzorem <math>\displaystyle x_k = (A^k)\cdot x</math>, lecz raczej korzystamy z
| |
| metody iteracyjnej
| |
| | |
| [title<nowiki>=</nowiki>Metoda potęgowa]
| |
| <math>\displaystyle x_0</math> <nowiki>=</nowiki> dowolny wektor startowy; k <nowiki>=</nowiki> 0;
| |
| while( !stop )
| |
| {
| |
| <math>\displaystyle y_k</math> <nowiki>=</nowiki> <math>\displaystyle Ax_{k-1}</math>;
| |
| <math>\displaystyle x_k</math> <nowiki>=</nowiki> <math>\displaystyle y_k/||y_k||_\infty</math>;
| |
| k++;
| |
| }
| |
| | |
| Warunek normowania ma m.in. na celu zapobieżenie powstawania nadmiaru i
| |
| niedomiaru (gdy <math>\displaystyle |\lambda_1| < 1</math>, to <math>\displaystyle ||A^kx|| \rightarrow 0</math>, a gdy
| |
| <math>\displaystyle |\lambda_1| > 1</math>, to <math>\displaystyle ||A^kx|| \rightarrow \infty</math>). Przy okazji,
| |
| <math>\displaystyle ||y_k||_\infty \rightarrow |\lambda_1|</math>, a więc mamy także sposób na wyznaczenie
| |
| przybliżenia dominującej wartości własnej.
| |
| | |
| Zazwyczaj jako warunek stopu wybiera się kryterium małej poprawki, <math>\displaystyle ||x_k -
| |
| x_{k-1}|| \leq \epsilon</math>, lub warunek małego residuum, <math>\displaystyle ||Ax_k - \lambda_{1,k}
| |
| x_k||\leq \epsilon</math>, gdzie <math>\displaystyle \lambda_{1,k}</math> jest przybliżeniem <math>\displaystyle \lambda_1</math>
| |
| dostępnym na <math>\displaystyle k</math>-tej iteracji.
| |
| | |
| {}{Zasada działania metody potęgowej}
| |
| | |
| Metoda potęgowa doskonale sprawdza się, gdy macierz <math>\displaystyle A</math> jest macierzą
| |
| rozrzedzoną --- np. w przypadku macierzy Google'a.
| |
| | |
| ====Odwrotna metoda potęgowa====
| |
| | |
| Zauważmy, że dla dowolnej macierzy kwadratowej <math>\displaystyle A</math> o wartościach własnych
| |
| <math>\displaystyle \lambda_k</math> i odpowiadających im wektorach własnych <math>\displaystyle q_k</math>, mamy:
| |
| * Macierz <math>\displaystyle A-\sigma I</math> ma wartości własne <math>\displaystyle \lambda_k - \sigma</math> oraz wektory
| |
| własne <math>\displaystyle q_k</math>,
| |
| * Jeśli dodatkowo <math>\displaystyle A</math> jest nieosobliwa, to macierz <math>\displaystyle A^{-1}</math> ma wartości
| |
| własne <math>\displaystyle 1/\lambda_k</math> oraz wektory własne <math>\displaystyle q_k</math>
| |
| | |
| Łącząc te dwie własności mamy, że
| |
| | |
| {{stwierdzenie|Transformacja widma macierzy||
| |
| | |
| Macierz <math>\displaystyle (A-\sigma I)^{-1}</math> (o ile istnieje),
| |
| to ma wartości własne równe <math>\displaystyle \frac{1}{\lambda_k - \sigma}</math> i wektory własne
| |
| identyczne z <math>\displaystyle A</math>.
| |
| }}
| |
| | |
| Skoro tak, to jeśli najbliższą <math>\displaystyle \sigma</math> wartością własną <math>\displaystyle A</math> jest <math>\displaystyle \lambda_j</math>,
| |
| wówczas metoda potęgowa zastosowana do macierzy <math>\displaystyle (A-\sigma I)^{-1}</math> zbiegnie do
| |
| <math>\displaystyle q_j</math>. To prowadzi do następującego algorytmu, odwrotnej metody potęgowej:
| |
| | |
| [title<nowiki>=</nowiki>Odwrotna metoda potęgowa]
| |
| <math>\displaystyle x_0</math> <nowiki>=</nowiki> dowolny wektor startowy; k <nowiki>=</nowiki> 0;
| |
| while( !stop )
| |
| {
| |
| Rozwiąż układ równań <math>\displaystyle (A-\sigma I)y_k = x_{k-1}</math>;
| |
| <math>\displaystyle x_k</math> <nowiki>=</nowiki> <math>\displaystyle y_k/||y_k||_\infty</math>;
| |
| k++;
| |
| }
| |
| | |
| ====Metoda Rayleigh====
| |
| | |
| Z własności metody potęgowej, metoda odwrotna potęgowa jest zbieżna tym
| |
| szybciej, im bliżej <math>\displaystyle \lambda_j</math> jest przesunięcie <math>\displaystyle \sigma</math> (w stosunku do
| |
| pozostałych wartości własnych). Dlatego dobrze byłoby --- dla zwiększenia
| |
| szybkości zbieżności iteracji --- poprawiać wartość przesunięcia <math>\displaystyle \sigma</math>,
| |
| korzystając z dotychczas wyznaczonego wektora <math>\displaystyle x_k \approx q_j</math> i ilorazu
| |
| Rayleigh:
| |
| | |
| <center><math>\displaystyle \lambda_j = \frac{q_j^TAq_j}{q_j^Tq_j} \approx \frac{x_k^TAx_k}{x_k^Tx_k}
| |
| </math></center>
| |
| | |
| [title<nowiki>=</nowiki>Metoda RQI (Rayleigh Quotient Iteration)]
| |
| <math>\displaystyle x_0</math> <nowiki>=</nowiki> dowolny wektor startowy; <math>\displaystyle \sigma_0</math> <nowiki>=</nowiki> przybliżenie <math>\displaystyle \lambda_j</math>; k <nowiki>=</nowiki> 0;
| |
| while( !stop )
| |
| {
| |
| Rozwiąż układ równań <math>\displaystyle (A-\sigma_k I)y_k = x_{k-1}</math>;
| |
| <math>\displaystyle x_k</math> <nowiki>=</nowiki> <math>\displaystyle y_k/||y_k||_2</math>;
| |
| <math>\displaystyle \sigma_{k+1}</math> <nowiki>=</nowiki> <math>\displaystyle x_k^TAx_k</math>;
| |
| k++;
| |
| }
| |
| | |
| (wybierając normowanie wektora <math>\displaystyle x</math> w normie euklidesowej upraszczamy co nieco
| |
| algorytm).
| |
| | |
| Wielką zaletą metody RQI jest jej szybkość zbiezności: kwadratowa gdy wartość
| |
| własna jest pojedyncza, a nawet sześcienna w przypadku macierzy symetrycznej.
| |
| | |
| Wadą metody RQI jest to, że na każdym jej kroku należy rozwiązywać układ równań
| |
| z ''inną'' macierzą.
| |
| | |
| {{uwaga|Gdy złe uwarunkowanie pomaga...||
| |
| | |
| Przez pewien czas numerycy odnosili się do tej metody z rezerwą,
| |
| twierdząc, i słusznie, że im lepszym przybliżeniem <math>\displaystyle q_j</math> będzie <math>\displaystyle \sigma_k</math>, tym
| |
| bardziej rośnie uwarunkowanie <math>\displaystyle A-\sigma_k I</math>, a tym samym --- błąd numerycznego
| |
| rozwiązywania układu z tą macierzą będzie coraz większy i metoda będzie tracić
| |
| stabilność. Tymczasem okazuje się, że --- choć rzeczywiście tak jest ---
| |
| wektor błędu ma kierunek praktycznie zgodny z kierunkiem poszukiwanego wektora
| |
| <math>\displaystyle q_j</math>, a tym samym tylko ''pomaga'' w zbieżności metody!
| |
| }}
| |
| | |
| ===Metoda dziel i rządź, metoda QR===
| |
| | |
| {}{Secular equation}
| |
| | |
| ===Biblioteki===
| |
| | |
| LAPACK zawiera w sobie kolekcję doskonałych narzędzi do rozwiązywania zadania
| |
| własnego. {WYmienic}
| |
| | |
| ARPACK rozwiązuje zadanie własne dla macierzy rozrzedzonych, zwłaszcza
| |
| symetrycznych.
| |
| | |
| Funkcja !eig! w Octave wyznacza wszystkie wartości własne (lub pary własne)
| |
| zadaniej gęstej macierzy. Jak dotąd, tylko MATLAB potrafi skorzystać z ARPACKa
| |
| dla wyznaczenia fragmentów widma macierzy rzadkiej, za pomocą funkcji
| |
| !eigs!.
| |