TC Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 216: | Linia 216: | ||
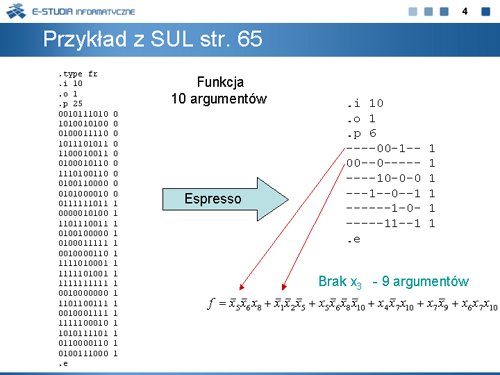
Wynik Espresso – 9 argumentów, 6 termów | Wynik Espresso – 9 argumentów, 6 termów | ||
<math>f=\overline{ | <math>f=\overline{x}_5\overline{x}_6x_8+\overline{x}_1\overline{x}_2\overline{x}_5+x_5\overline{x}_6\overline{x}_8\overline{x}_{10}+x_4\overline{x}_7x_{10}+x_7\overline{x}_9+x_6x_7x_{10}</math> | ||
Wynik Pandora – 7 argumentów, 5 termów | Wynik Pandora – 7 argumentów, 5 termów | ||
<math>f=\overline{ | <math>f=\overline{x}_1\overline{x}_2\overline{x}_7+x_1x_2x_4+\overline{x}_1x_{10}+\overline{x}_1\overline{x}_4\overline{x}_6+x_7\overline{x}_9</math> | ||
|} | |} | ||
| Linia 238: | Linia 238: | ||
|valign="top"|Możemy więc porównać wynik minimalizacji programem Espresso: | |valign="top"|Możemy więc porównać wynik minimalizacji programem Espresso: | ||
<math>f=\overline{ | <math>f=\overline{x}_2x_{14}\overline{x}_{19}x_{21}+x_7\overline{x}_8\overline{x}_{12}+x_5x_8\overline{x}_{20}</math> | ||
z minimalizacją systematyczną wspomaganą procedurą redukcji argumentów. | z minimalizacją systematyczną wspomaganą procedurą redukcji argumentów. | ||
<math>f=\overline{ | <math>f=\overline{x}_2\overline{x}_4x_9\overline{x}_{19}+\overline{x}_2x_4\overline{x}_9+x_2x_{19}\overline{x}_{20}</math> | ||
|} | |} | ||
<hr width="100%"></math> | <hr width="100%"></math> | ||
Wersja z 21:41, 28 sie 2006

|
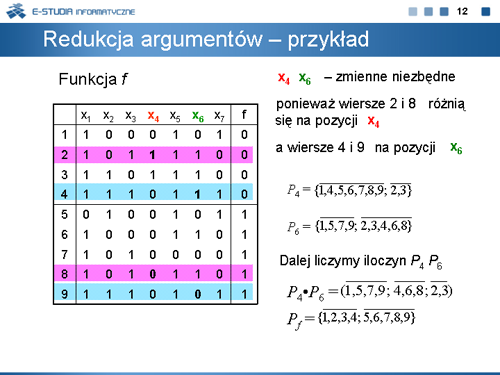
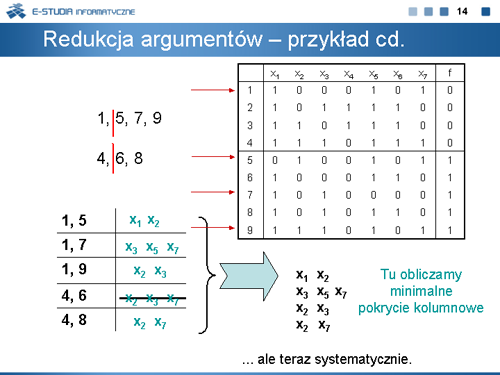
Redukcja argumentów |
|
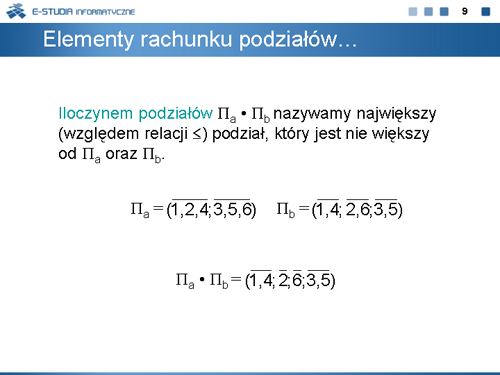
Iloczynem podziałów nazywamy największy (względem relacji ) podział, który jest nie większy od oraz .
Symetrycznie, sumą nazywamy najmniejszy podział nie mniejszy od oraz .
|

|
Rachunek podziałów zastosujemy do reprezentacji funkcji boolowskich. Dla funkcji EXTL, której tablicę prawdy powtarzamy na niniejszej planszy jej zapis w postaci podziałów jest następujący:
|

|
Porównajmy wyniki tak przeprowadzanych minimalizacji.
Wynik Espresso – 9 argumentów, 6 termów
Wynik Pandora – 7 argumentów, 5 termów
|

|
Możemy więc porównać wynik minimalizacji programem Espresso:
z minimalizacją systematyczną wspomaganą procedurą redukcji argumentów.
|
</math>