TC Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 101: | Linia 101: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd10.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd10.png]] | ||
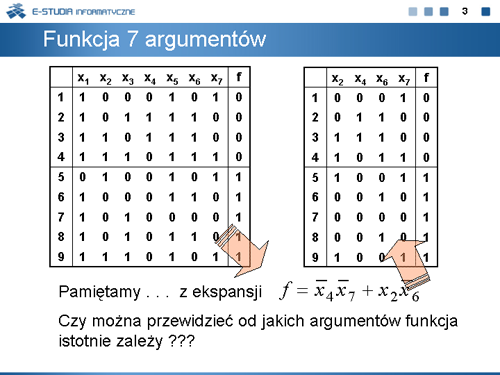
|valign="top"| | |valign="top"|Rachunek podziałów zastosujemy do reprezentacji funkcji boolowskich. Dla funkcji EXTL, której tablicę prawdy powtarzamy na niniejszej planszy jej zapis w postaci podziałów jest następujący: | ||
<math>P_1=(\overline{5}; \overline{1,2,3,4,6,7,8,9})</math> | |||
<math>P_2=(\overline{1,2,6,7,8}; \overline{3,4,5,9})</math> | |||
<math>P_3=(\overline{1,3,5,6}; \overline{2,4,7,8,9})</math> | |||
<math>P_4=(\overline{1,4,5,6,7,8,9}; \overline{2,3})</math> | |||
<math>P_5=(\overline{7}; \overline{1,2,3,4,5,6,8,9})</math> | |||
<math>P_6=(\overline{1,5,7,9}; \overline{2,3,4,6,8})</math> | |||
<math>P_7=(\overline{2,3,6,7,8}; \overline{1,4,5,9})</math> | |||
<math>P_f=(\overline{1,2,3,4}; \overline{5,6,7,8,9})</math> | |||
|} | |} | ||
| Linia 108: | Linia 125: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd11.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd11.png]] | ||
|valign="top"| | |valign="top"|Jeżeli wektory <math>X_a\,</math> oraz <math>X_b\,</math>: <math>f\,(X_a)\neq f\,(X_b)</math> , różnią się dokładnie dla jednej zmiennej to nazywamy ją zmienną niezbędną. Sens fizyczny zmiennej niezbędnej wynika z faktu, że usunięcie kolumny odpowiadającej tej zmiennej w tablicy prawdy tworzy tablicę, w której dwa takie same wektory mają różne wartości (są sprzeczne). | ||
|} | |} | ||
| Linia 115: | Linia 133: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd12.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd12.png]] | ||
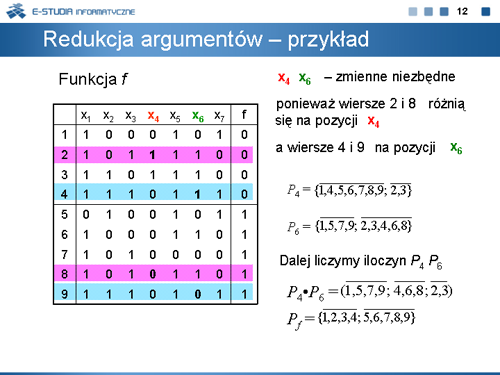
|valign="top"| | |valign="top"|Na przykładzie funkcji EXTL wyjaśniamy poszukiwanie zmiennych niezbędnych. | ||
Zmiennymi niezbędnymi tej funkcji są <math>x_4\,</math> , <math>x_6\,</math>. Co łatwo sprawdzić, gdyż wiersze o numerach 2 i 8 (zaznaczone kolorem różowym) różnią się wyłącznie na pozycji <math>x_4\,</math>, natomiast wiersze 4 i 9 (zaznaczone kolorem niebieskim) różnią się tylko na pozycji <math>x_6\,</math>. | |||
Po wyznaczeniu zmiennych niezbędnych obliczamy iloczyn podziałów <math>P = P_4\cdot P_6\,</math> . | |||
|} | |} | ||
| Linia 122: | Linia 144: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd13.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd13.png]] | ||
|valign="top"| | |valign="top"|Iloczyn podziałów wyznaczonych przez zmienne niezbędne ma bardzo ważną interpretację. | ||
Zauważmy, że kolejne bloki iloczynu <math>P = (B_1,...,B_3)\,</math> są <math>B_1=\left \{1,5,7,9 \right \}</math> , <math>B_2=\left \{4,6,8\right \}</math> , <math>B_3 = {2,3\}</math>.Blok <math>B_3\,</math> jest zawarty w jednym bloku podziału <math>P_f\,</math>. Ale bloki <math>B_1\,</math> i <math>B_2\,</math> zawierają elementy należące do dwóch różnych bloków podziału <math>P_f\,</math>, czyli same zmienne <math>x_4\,</math> , <math>x_6\,</math> nie wystarczają do oddzielenia wektorów prawdziwych od fałszywych realizowanej funkcji. | |||
|} | |} | ||
| Linia 129: | Linia 154: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd14.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd14.png]] | ||
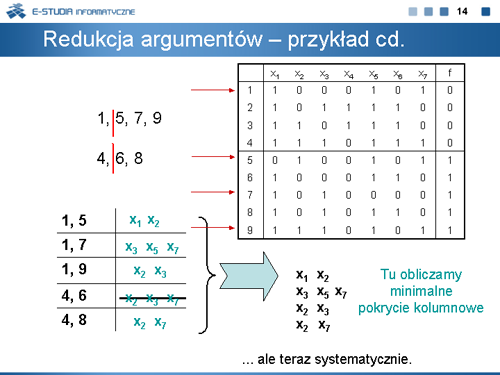
|valign="top"| | |valign="top"|Zatem należy się zastanowić jakie argumenty należy dołożyć do argumentów niezbędnych, aby zapewnić jednoznaczną realizację tej funkcji. Obserwując zbiory <math>B_1=\left \{1,5,7,9\right \}</math>, <math>B_2=\left \{4,6,8\right \}</math> , łatwo stwierdzić, że wystarczy w tym celu dobrać takie argumenty, aby „oddzielić” wektory (wiersze) o numerach 1 od 5, 7, 9 oraz 4 od 6, 8. Zatem należy oddzielić 1 od 5, 1 od 7 itd. Zapisujemy zbiory argumentów, dla których różnią się wiersze 1 i 5, 1 i 7 itd. w formie stosownej tabelki (jak na planszy). W tabelce tej zbiór w wierszu oznaczonym 4, 6 pokrywa zbiór z wiersza 1, 9. Zatem wiersz „większy” usuwamy. | ||
Ogólnie usuwamy każdy zbiór <math>Z\,</math> dla którego istnieje <math>Z': Z'\subseteq Z\,</math>. Tak wyznaczana tabelka (w szczególności) zredukowana może być interpretowana jako zadanie obliczania minimalnego pokrycia kolumnowego. | |||
|} | |} | ||
| Linia 136: | Linia 164: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd15.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd15.png]] | ||
|valign="top"| | |valign="top"|Chcąc zatem obliczyć minimalne zbiory argumentów zapisujemy zredukowaną tabelkę w postaci wyrażenia boolowskiego typu „iloczyn sum”. Kolejną czynnością jest przekształcenie „iloczynu sum” w wyrażenie typu „suma iloczynów” W czynności tej oczywiście stosujemy zasady algebry Boole’a. I w rezultacie uzyskujemy wyrażenie: | ||
<math>x_2x_3+x_2x_5+x_2x_7+x_1x_3x_7+</math> | |||
które interpretujemy następująco. Wszystkie składniki tego wyrażenia o minimalnej liczbie czynników (zmiennych <math>x_i\,</math>) reprezentują minimalne zbiory argumentów, które łącznie ze zmiennymi niezbędnymi tworzą minimalne zbiory argumentów wystarczające do realizacji funkcji: | |||
<math>\left \{x_2, x_3, x_4, x_6\right \}, \left \{x_2, x_3, x_5, x_6\right \}, \left \{x_2, x_3, x_6, x_7\right \} </math> . | |||
Stąd wniosek, że siedmio-argumentowa funkcja f w rzeczywistości jest zależna wyłącznie od czterech argumentów. | |||
|} | |} | ||
| Linia 143: | Linia 180: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd16.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd16.png]] | ||
|valign="top"| | |valign="top"|Zauważmy też, że ostatnie z podanych rozwiązań oznacza usunięcie z tablicy funkcji <math>f\,</math> kolumn odpowiadających zmiennym <math>x1, x3, x5\,</math> . W rezultacie uzyskujemy tablicę, której wymiary umożliwiają zastosowanie nawet najprostszej metody minimalizacji jaką jest tablica Karnaugha. | ||
|} | |} | ||
| Linia 150: | Linia 188: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd17.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd17.png]] | ||
|valign="top"| | |valign="top"|Omówioną metodę zrealizowaną w postaci oddzielnego modułu oprogramowania można traktować jako procedurę wspomagająca metodę i program Espresso. W celu przekonania się o skuteczności wspomagania minimalizacji funkcji boolowskich dodatkową procedurą redukcji argumentów omówimy kilka eksperymentów wykonanych programami Espresso i Pandor. W eksperymentach tych dokonamy minimalizacji dwóch typowych funkcji boolowskich: TL27 i KAZ. W szczególności porównamy wyniki minimalizacji uzyskane programem Espresso z wynikami uzyskanymi przy wspomaganiu minimalizacji dodatkową procedura redukcji argumentów. | ||
|} | |} | ||
| Linia 157: | Linia 196: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd18.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd18.png]] | ||
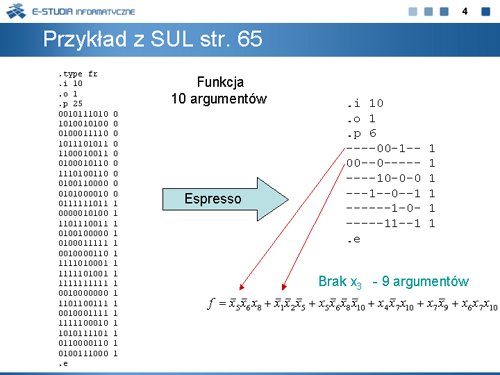
|valign="top"| | |valign="top"|Eksperyment z funkcją TL27. Na planszy z lewej strony podany jest plik wejściowy programu Espresso z zapisaną funkcją TL27. Z prawej strony tej planszy podany jest wynik minimalizacji tej funkcji programem Espresso. Jak widać espresso minimalizuje tę funkcję do 6 termów (składników iloczynowych) z łączną liczbą 9 argumentów. | ||
|} | |} | ||
| Linia 164: | Linia 204: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd19.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd19.png]] | ||
|valign="top"| | |valign="top"|Za pomocą programu Pandor można obliczyć, że funkcja ta ma 10 rozwiązań dla minimalnych zbiorów argumentów. Jedno z tych rozwiązań jest podane na planszy. Jest zrozumiałe, że funkcja o mniejszej liczbie argumentów jest „łatwiejsza” do minimalizacji. Zatem tak zredukowaną funkcję można poddać obliczeniom za pomocą programu Pandor. | ||
|} | |} | ||
| Linia 171: | Linia 212: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd20.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd20.png]] | ||
|valign="top"| | |valign="top"|Porównajmy wyniki tak przeprowadzanych minimalizacji. | ||
Wynik Espresso – 9 argumentów, 6 termów | |||
<math>f=</math> | |||
|} | |} | ||
Wersja z 21:19, 28 sie 2006

|
Redukcja argumentów |
|
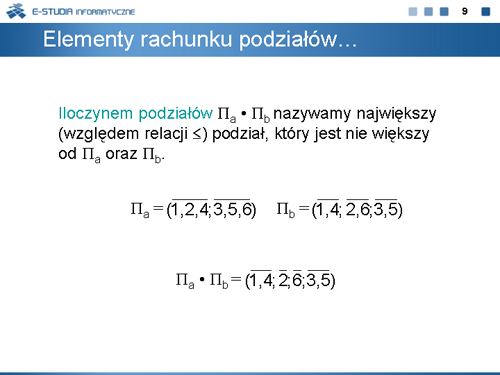
Iloczynem podziałów nazywamy największy (względem relacji ) podział, który jest nie większy od oraz .
Symetrycznie, sumą nazywamy najmniejszy podział nie mniejszy od oraz .
|

|
Rachunek podziałów zastosujemy do reprezentacji funkcji boolowskich. Dla funkcji EXTL, której tablicę prawdy powtarzamy na niniejszej planszy jej zapis w postaci podziałów jest następujący:
|

|
Porównajmy wyniki tak przeprowadzanych minimalizacji.
Wynik Espresso – 9 argumentów, 6 termów
|

|

|