TC Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 55: | Linia 55: | ||
|valign="top"|''Podziałem'' na zbiorze <math>S\,</math> jest system zbiorów <math>\pi=\left \{ Bi \right\}\,</math>, którego bloki są rozłączne, czyli | |valign="top"|''Podziałem'' na zbiorze <math>S\,</math> jest system zbiorów <math>\pi=\left \{ Bi \right\}\,</math>, którego bloki są rozłączne, czyli | ||
<math>B_i\cap B_j=\varnothing</math> , jeśli tylko <math>i\neq j</math> . | :<math>B_i\cap B_j=\varnothing</math> , jeśli tylko <math>i\neq j</math> . | ||
Na przykład dla <math>S = \left \{1,2,3,4,5,6\right \} \,</math> , <math>\left \{\left \{1,2\right \} , \left \{3,5\right \}, \left \{4,6\right \}\right \} jest podziałem na <math>S\,</math>, co zapisujemy: | Na przykład dla <math>S = \left \{1,2,3,4,5,6\right \} \,</math> , <math>\left \{\left \{1,2\right \} , \left \{3,5\right \}, \left \{4,6\right \}\right \}</math> jest podziałem na <math>S\,</math>, co zapisujemy: | ||
:<math>\pi=(\overline{1,2};\overline{3,4};\overline{5,6})</math> | :<math>\pi=(\overline{1,2};\overline{3,4};\overline{5,6})</math> | ||
| Linia 71: | Linia 71: | ||
|valign="top"|Powiemy, że podział <math>\pi_1\,</math> jest nie większy od <math>\pi_2\,</math> (co oznaczamy: <math>\pi_1\le \pi_2</math>), jeśli każdy blok z <math>\pi_1\,</math> jest zawarty w pewnym bloku z <math>\pi_2\,</math>. | |valign="top"|Powiemy, że podział <math>\pi_1\,</math> jest nie większy od <math>\pi_2\,</math> (co oznaczamy: <math>\pi_1\le \pi_2</math>), jeśli każdy blok z <math>\pi_1\,</math> jest zawarty w pewnym bloku z <math>\pi_2\,</math>. | ||
Wprowadzamy oznaczenia odpowiednio dla podziału najmniejszego <math>\pi (0)\,</math> oraz największego <math>\pi (1)\,</math>. Podział <math>\pi (0)\,</math> jest podziałem, którego bloki są elementami zbioru <math>S\,</math>. Podział <math>\pi (1)\,</math> jest podziałem o jednym bloku wyczerpującym cały zbiór <math>S\,</math>. Na przykład: dla <math>S = \left\{1, 2, 3}\right\}\,</math>, | Wprowadzamy oznaczenia odpowiednio dla podziału najmniejszego <math>\pi (0)\,</math> oraz największego <math>\pi (1)\,</math>. Podział <math>\pi (0)\,</math> jest podziałem, którego bloki są elementami zbioru <math>S\,</math>. Podział <math>\pi (1)\,</math> jest podziałem o jednym bloku wyczerpującym cały zbiór <math>S\,</math>. Na przykład: dla <math>S = \left\{1, 2, 3}\right\}\,</math>, <math>\pi (0) = \left\{\overline{1}, \overline{2}, \overline{3}}\right\}\,</math> , <math>\pi (1) = \left\{\overline{1,2,3}}\right\}\,</math> . | ||
|} | |} | ||
| Linia 79: | Linia 79: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd9.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd9.png]] | ||
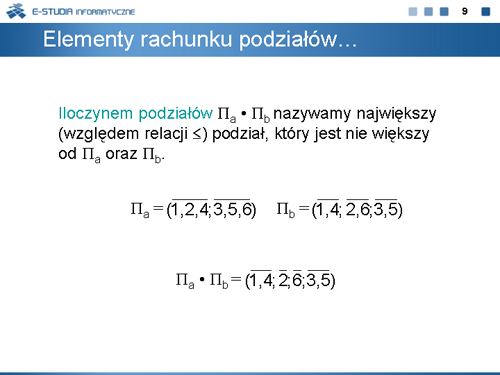
|valign="top"| | |valign="top"|Iloczynem podziałów <math>\pi_1\bullet \pi_2\,</math> nazywamy największy (względem relacji <math>\le\,</math>) podział, który jest nie większy od <math>\pi_1\,</math> oraz <math>\pi_2\,</math>. | ||
<math>\Pi_a=(\overline{1,2,4}; \overline{3,5,6})</math> | |||
<math>\Pi_b=(\overline{1,4}; \overline{2,6}; \overline{3,5})</math> | |||
<math>\Pi_1\bullet \Pi_2=(\overline{1,4}; \overline{2}; \overline{6}; \overline{3,5})</math> | |||
Symetrycznie, ''sumą <math>\pi_1+ \pi_2\,</math>'' nazywamy najmniejszy podział nie mniejszy od <math>\pi_1\,</math> oraz <math>\pi_2\,</math>. | |||
<math>\Pi_a=(\overline{1,2}; \overline{3,4}; \overline{5,6}; \overline{7,8,9})</math> | |||
<math>\Pi_b=(\overline{1,6}; \overline{2,3}; \overline{4,5}; \overline{7,8}; \overline{9})</math> | |||
<math>\Pi_1+ \Pi_2=(\overline{1,2,3,4,5,6}; \overline{7,8,9})</math> | |||
|} | |} | ||
Wersja z 20:50, 28 sie 2006

|
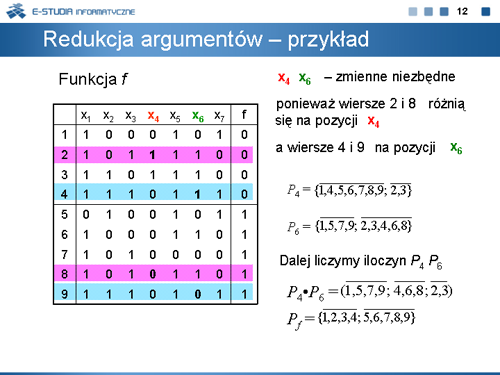
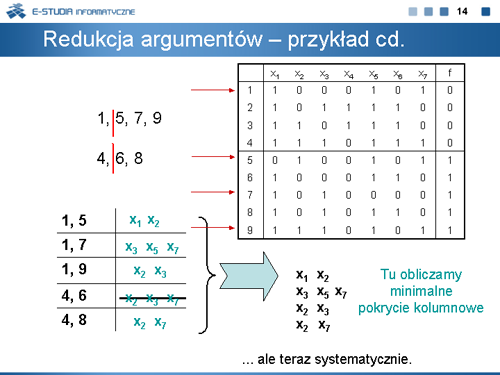
Redukcja argumentów |
|
Iloczynem podziałów nazywamy największy (względem relacji ) podział, który jest nie większy od oraz .
Symetrycznie, sumą nazywamy najmniejszy podział nie mniejszy od oraz .
|

|

|
|

|
|

|

|

|

|

|

|

|

|