MN04: Różnice pomiędzy wersjami
mNie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 46: | Linia 46: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
<div style="font-size:smaller">Kluczem do efektywnej implementacji w Octave jest przeprowadzenie | <div style="font-size:smaller; background-color:#cfd">Kluczem do efektywnej implementacji w Octave jest przeprowadzenie | ||
iteracji Newtona na ''wszystkich pikselach jednocześnie''. W tym celu musisz | iteracji Newtona na ''wszystkich pikselach jednocześnie''. W tym celu musisz | ||
skorzystać z prowadzenia działań na całych macierzach.</div> | skorzystać z prowadzenia działań na całych macierzach.</div> | ||
Wersja z 16:50, 28 sie 2006
Uwaga: przekonwertowane latex2mediawiki; prawdopodobnie trzeba wprowadzi? poprawki
Ćwiczenia: równania nieliniowe skalarne
Ćwiczenie Metoda Newtona może być zbieżna globalnie
Wykaż, że jeśli jest rosnąca i wypukła na oraz dla , to metoda Newtona startująca z jest zbieżna.
Ćwiczenie Fraktale
Ćwiczenie Pierwiastkowanie
Ćwiczenie Odwrotność bez dzielenia
Aby wyznaczyć dla bez dzielenia(!), można zastosować metodę Newtona do funkcji . Pokaż, że na -tym kroku iteracji,
Dla jakich metoda będzie zbieżna do , a dla jakich nie? Oceń, ile iteracji potrzeba do spełnienia warunku , gdy ,
Ćwiczenie
Zaimplementuj metodę bisekcji. Sprawdź, jak będzie działać m.in. dla funkcji
- ,
- ,
- (wzór A),
- (wzór B),
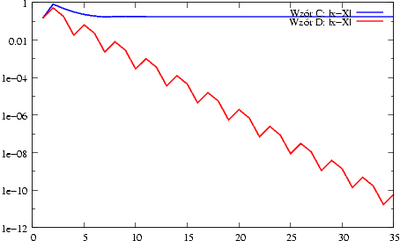
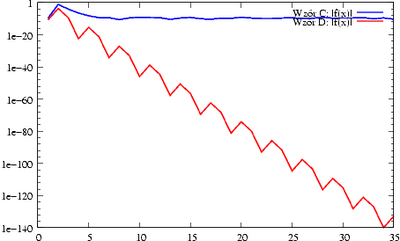
- (wzór C),
- (wzór D),
gdy tolerancję błędu zadasz na poziomie .
Jak wyjaśnić te wyniki? Czy możesz już być pewna, że masz dobrą implementację?
Ćwiczenie