TC Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd1.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd1.png]] | ||
|valign="top"| | |valign="top"|Minimalizacja funkcji boolowskich metodą tablic Karnaugha. | ||
|} | |} | ||
| Linia 8: | Linia 8: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd2.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd2.png]] | ||
|valign="top"| | |valign="top"|Zasygnalizowany w poprzednim wykładzie proces minimalizacji funkcji boolowskich ma ogromne znaczenie w technice cyfrowej. Znaczenie to zostało spotęgowane możliwościami realizacji układów logicznych w strukturach scalonych o złożoności milionów bramek logicznych. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 17: | Linia 15: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd3.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd3.png]] | ||
|valign="top"| | |valign="top"|Wypracowano wiele metod minimalizacji funkcji boolowskich. Najbardziej znaną i uznawaną za najskuteczniejszą jest metoda ESPRESSO opracowana w latach 80. na Uniwersytecie Kalifornijskim w Berkeley. Ze względu na ograniczony zakres wykładu omówimy wyłącznie metodę tablic Karnaugha oraz metodę ekspansji (przykładową procedurę Espresso). | ||
|} | |} | ||
| Linia 24: | Linia 22: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd4.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd4.png]] | ||
|valign="top"| | |valign="top"|W metodzie Karnaugha każda kratka odpowiedniej tablicy (zwanej tablicą Karnaugha) odpowiada wektorowi zmiennych binarnych. Można więc powiedzieć, że ciąg wartości tych zmiennych tworzy adres kratki. Kratki są ponumerowane w taki sposób, że numer i jest liczbą dziesiętną odpowiadającą kombinacji zmiennych (wektorowi zero-jedynkowemu) traktowanej jako liczba dwójkowa. W poszczególnych kratkach wpisane są wartości funkcji, tj. 0 lub 1 przyjmowanej przez funkcję dla tej kombinacji lub symbol „–”, jeżeli funkcja nie jest określona. W tablicy Karnaugha różniącym się tylko o negację pełnym iloczynom przyporządkowane są leżące obok siebie pola tablicy (sąsiednie kratki), które się łączy (skleja) odpowiednią pętelką. Korzysta się z faktu, że dla dowolnego A: | ||
: <math>A \overline{x}+Ax=A</math> | |||
|} | |} | ||
| Linia 31: | Linia 32: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd5.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd5.png]] | ||
|valign="top"| | |valign="top"|Dla uzyskania efektu sąsiedztwa współrzędne pól opisuje się tzw. kodem Gray’a. | ||
|} | |} | ||
| Linia 38: | Linia 39: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd6.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd6.png]] | ||
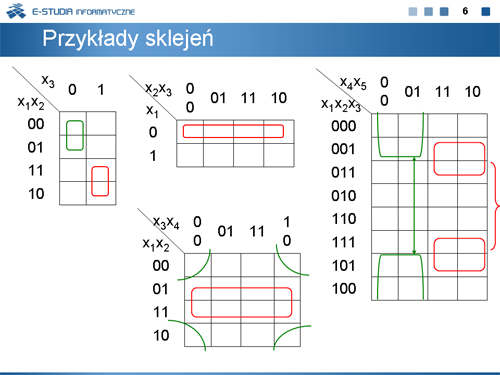
|valign="top"| | |valign="top"|Na planszy pokazane są przykłady łączenia (sklejania) kratek tablicy Karnaugha. | ||
|} | |} | ||
| Linia 45: | Linia 46: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd7.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd7.png]] | ||
|valign="top"| | |valign="top"|Kolejny przykład ilustruje wykorzystanie zasady łączenia kratek do graficznej minimalizacji funkcji boolowskiej. | ||
|} | |} | ||
| Linia 52: | Linia 53: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd8.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd8.png]] | ||
|valign="top"| | |valign="top"|Wpisywanie funkcji do tablicy Karnaugha ułatwia numeracja kratek. Podajemy przykłady tablic Karnaugha z ponumerowanymi kratkami. | ||
|} | |} | ||
| Linia 59: | Linia 60: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd9.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd9.png]] | ||
|valign="top"| | |valign="top"|Oraz stosujemy tę metodę do funkcji z poprzedniego przykładu. | ||
|} | |} | ||
| Linia 66: | Linia 67: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd10.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd10.png]] | ||
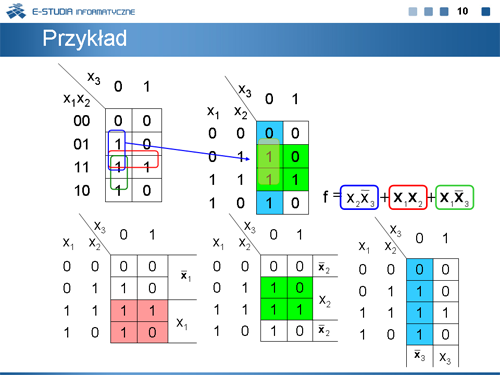
|valign="top"| | |valign="top"|Niestety zakreślanie pętelek i kojarzenie z nimi odpowiednich iloczynów jest trudniejsze. Omawiamy ten proces na bardziej skomplikowanym przykładzie, w którym kolorami zaznaczamy odpowiednie pola tablicy Karnaugha. Pokrywanie się tych pól określa odpowiedni iloczyn zmiennych prostych lub zanegowanych. | ||
|} | |} | ||
| Linia 73: | Linia 74: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd11.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd11.png]] | ||
|valign="top"| | |valign="top"|Na tym przykładzie trenujemy cały proces minimalizacji funkcji metodą tablic Karnaugha. | ||
|} | |} | ||
| Linia 80: | Linia 81: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd12.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd12.png]] | ||
|valign="top"| | |valign="top"|Pojęciem podstawowym w procesie minimalizacji jest pojęcie implikantu. Implikant funkcji boolowskiej <math>f</math> jest to iloczyn literałów (czyli zmiennych prostych lub zanegowanych) o następującej własności: dla wszystkich kombinacji wartości zmiennych, dla których implikant jest równy jedności, również funkcja <math>f</math> jest równa jedności. | ||
Prosty implikant jest to implikant, który zmniejszony o dowolny literał przestaje być implikantem. | |||
|} | |} | ||
| Linia 87: | Linia 90: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd13.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd13.png]] | ||
|valign="top"| | |valign="top"|Pojęcie implikantu można zinterpretować na tablicy Karnaugha. | ||
|} | |} | ||
| Linia 94: | Linia 97: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd14.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd14.png]] | ||
|valign="top"| | |valign="top"|Omówimy teraz zapis funkcji boolowskiej w kanonicznej formie sumacyjnej oraz kanonicznej formie iloczynowej. | ||
|} | |} | ||
| Linia 101: | Linia 104: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd15.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd15.png]] | ||
|valign="top"| | |valign="top"|Podajemy ogólny wzór na kanoniczną formę sumacyjną oraz sposób tworzenia tej formy dla przykładowej funkcji. KFS można utworzyć bezpośrednio z tablicy prawdy przez wybranie wierszy, dla których wartość funkcji wynosi 1, utworzenie dla każdego takiego wiersza iloczynu pełnego, oraz utworzenie sumy iloczynów pełnych. | ||
|} | |} | ||
| Linia 108: | Linia 111: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd16.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd16.png]] | ||
|valign="top"| | |valign="top"|Podajemy ogólny wzór na kanoniczną formę iloczynową oraz sposób tworzenia tej formy dla przykładowej funkcji. W tym przypadku synteza funkcji sprowadza się do wybrania wierszy, dla których wartość funkcji wynosi 0, utworzenia dla każdego takiego wiersza sumy pełnej oraz utworzenia iloczynu sum pełnych. | ||
|} | |} | ||
| Linia 115: | Linia 118: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd17.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd17.png]] | ||
|valign="top"| | |valign="top"|Formy kanoniczne są stosowane do uzyskiwania różnych realizacji bramkowych funkcji boolowskich. Są to: | ||
*realizacja AND-OR, | |||
*realizacja NAND, | |||
*realizacja OR-AND, | |||
*realizacja NOR. | |||
|} | |} | ||
| Linia 122: | Linia 130: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd18.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd18.png]] | ||
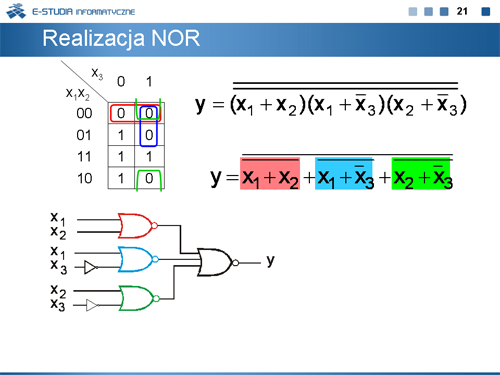
|valign="top"| | |valign="top"|Kolejne plansze ilustrują sposób tworzenia takich realizacji. | ||
|} | |} | ||
| Linia 150: | Linia 158: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd22.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd22.png]] | ||
|valign="top"| | |valign="top"|Oto bardziej skomplikowany przykład realizacji iloczynowej. | ||
|} | |} | ||
| Linia 157: | Linia 165: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd23.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd23.png]] | ||
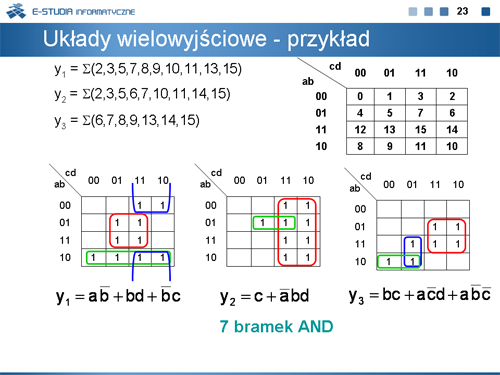
|valign="top"| | |valign="top"|W dotychczasowych przykładach minimalizowane były pojedyncze funkcje boolowskie, dla których – w celu uzyskania rozwiązania z minimalnym kosztem – tworzone były wyłącznie implikanty proste. W ogólnym przypadku minimalizacji zespołów funkcji boolowskich tworzenie minimalnego rozwiązania wyłącznie na podstawie implikantów prostych nie zawsze prowadzi do najlepszego rezultatu końcowego. Problem ilustrujemy następującym przykładem zespołu funkcji: | ||
: <math>y_1 = \sum(2,3,5,7,8,9,10,11,13,15)</math> | |||
: <math>y_2 = \sum(2,3,5,6,7,10,11,14,15)</math> | |||
: <math>y_3 = \sum(6,7,8,9,13,14,15)</math> | |||
Po zakreśleniu „pętelek” obejmujących implikanty proste uzyskujemy następujące wyrażenia boolowskie: | |||
: <math>y_1=a \bar b + bd + \bar b c</math> | |||
: <math>y_2=c+\bar a bd</math> | |||
: <math>y_3=bc+a \bar c d + a \bar b \bar c</math> | |||
Realizacja tych wyrażeń wymaga zastosowania 7 bramek AND i 3 bramek OR. | |||
|} | |} | ||
| Linia 164: | Linia 185: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M3_Slajd24.png]] | |valign="top" width="450px"|[[Grafika:TC_M3_Slajd24.png]] | ||
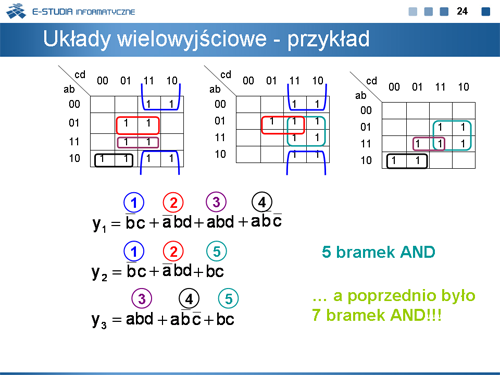
|valign="top"| | |valign="top"|Znacznie lepszą realizację uzyskamy dokonując minimalizacji w sposób przedstawiony w tablicach na niniejszej planszy. Pętelki w tych tablicach zakreślamy tak, aby uzyskiwać implikanty wspólne dla co najmniej dwóch spośród trzech funkcji. Spełnienie tego warunku wymusza zakreślanie pętelek wokół grup kratek reprezentujących implikanty, które nie są implikantami prostymi. W rezultacie uzyskujemy następujące wyrażenia: | ||
: <math>y_1=\bar b c + \bar a bd + abd + a \bar b \bar c</math> | |||
: <math>y_2=\bar b c + \bar a bd + bc</math> | |||
: <math>y_3=abd + a \bar b \bar c + bc</math> | |||
Realizacja powyższych wyrażeń łącznie, mimo pozornie większego skomplikowania dla poszczególnych funkcji, jest oszczędniejsza niż poprzednio; całość wymaga bowiem zastosowania 5 bramek AND i trzech bramek OR. | |||
|} | |} | ||
Aktualna wersja na dzień 13:43, 28 sie 2006

|
Minimalizacja funkcji boolowskich metodą tablic Karnaugha. |

|
Dla uzyskania efektu sąsiedztwa współrzędne pól opisuje się tzw. kodem Gray’a. |
|
Na planszy pokazane są przykłady łączenia (sklejania) kratek tablicy Karnaugha. |
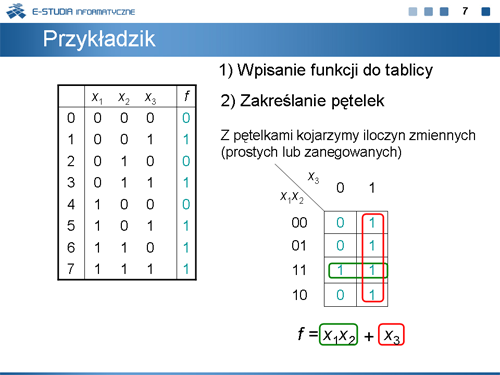
|
Kolejny przykład ilustruje wykorzystanie zasady łączenia kratek do graficznej minimalizacji funkcji boolowskiej. |

|
Wpisywanie funkcji do tablicy Karnaugha ułatwia numeracja kratek. Podajemy przykłady tablic Karnaugha z ponumerowanymi kratkami. |

|
Oraz stosujemy tę metodę do funkcji z poprzedniego przykładu. |

|
Na tym przykładzie trenujemy cały proces minimalizacji funkcji metodą tablic Karnaugha. |
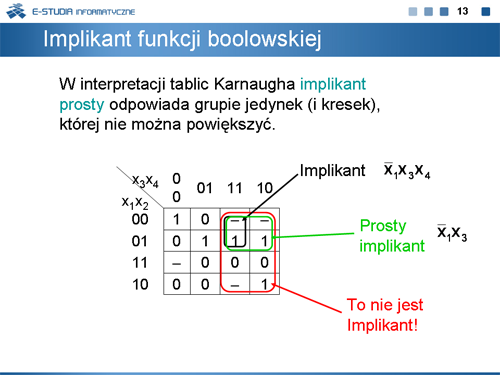
|
Pojęcie implikantu można zinterpretować na tablicy Karnaugha. |

|
Omówimy teraz zapis funkcji boolowskiej w kanonicznej formie sumacyjnej oraz kanonicznej formie iloczynowej. |

|
Formy kanoniczne są stosowane do uzyskiwania różnych realizacji bramkowych funkcji boolowskich. Są to:
|

|
Kolejne plansze ilustrują sposób tworzenia takich realizacji. |
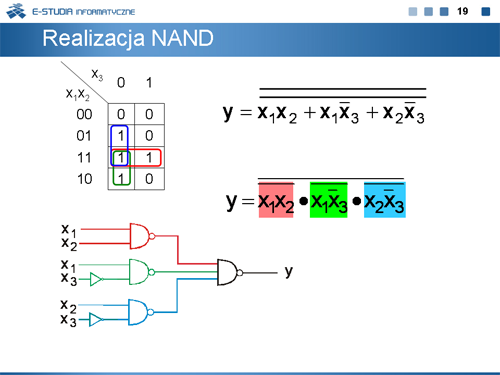
|
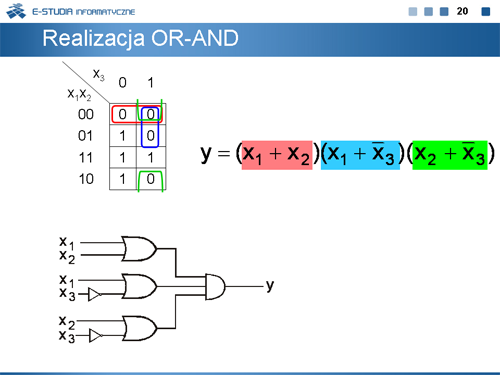
|
|

|
Oto bardziej skomplikowany przykład realizacji iloczynowej. |