PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 502: | Linia 502: | ||
: <math>u_L(t)=L\frac{di}{dt}=Ee^{-\frac{R}{2L}t}(1-\frac{R}{2L}t)</math> | : <math>u_L(t)=L\frac{di}{dt}=Ee^{-\frac{R}{2L}t}(1-\frac{R}{2L}t)</math> | ||
Napięcie na kondensatorze w stanie nieustalonym można uzyskać bezpośrednio z prawa napięciowego Kirchhoffa napisanego dla obwodu | Napięcie na kondensatorze w stanie nieustalonym można uzyskać bezpośrednio z prawa napięciowego Kirchhoffa napisanego dla obwodu RLC po przełączeniu. Mianowicie | ||
<math>u_C(t)=E-Ri_L(t)-u_L(t)=E-E^{-\frac{R}{2L}t}(1+\frac{R}{2L}t) </math> | : <math>u_C(t)=E-Ri_L(t)-u_L(t)=E-E^{-\frac{R}{2L}t}(1+\frac{R}{2L}t) </math> | ||
|} | |} | ||
| Linia 511: | Linia 511: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd26.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd26.png]] | ||
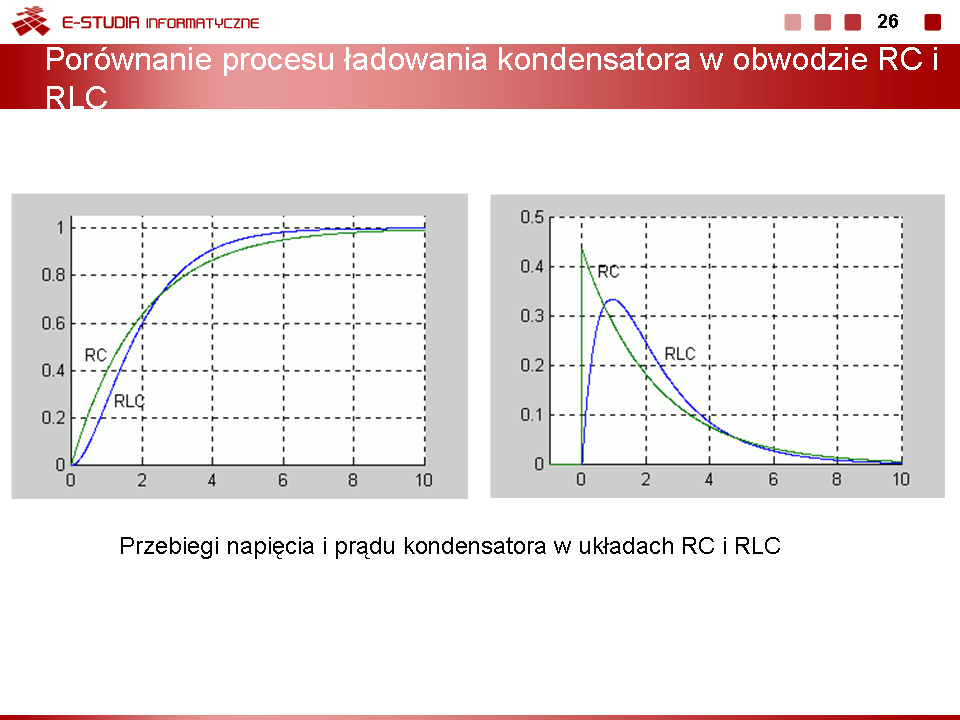
|valign="top"|Na slajdzie | |valign="top"|Na slajdzie obok przedstawiono przebieg ładowania kondensatora w stanie aperiodycznym krytycznym na tle przypadku aperiodycznego. | ||
Jedyna różnica występuje w czasie trwania stanu przejściowego, który najszybciej zanika dla przypadku krytycznego. Charakter przebiegu prądu i napięć w obwodzie dla przypadku aperiodycznego krytycznego jest podobny do zwykłego przypadku aperiodycznego, z tym, że najszybciej uzyskiwany jest stan ustalony (stan przejściowy trwa najkrócej z możliwych). | Jedyna różnica występuje w czasie trwania stanu przejściowego, który najszybciej zanika dla przypadku krytycznego. Charakter przebiegu prądu i napięć w obwodzie dla przypadku aperiodycznego krytycznego jest podobny do zwykłego przypadku aperiodycznego, z tym, że najszybciej uzyskiwany jest stan ustalony (stan przejściowy trwa najkrócej z możliwych). | ||
| Linia 522: | Linia 522: | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd27.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd27.png]] | ||
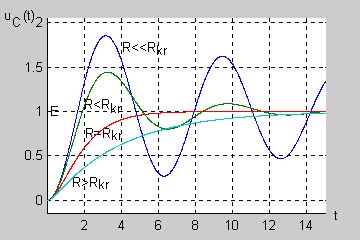
|valign="top"|'''Przypadek oscylacyjny''' | |valign="top"|'''Przypadek oscylacyjny''' | ||
Przypadek oscylacyjny zmian prądu i napięć w obwodzie szeregowym RLC występuje przy spełnieniu warunku <math>R<2\sqrt{\frac{L}{C}}</math> a więc przy małych wartościach rezystancji R. W tym przypadku oba bieguny są zespolone. Dla wyznaczenia postaci czasowej prądu wygodniej jest zastosować metodę tablic transformat. W tym celu należy przekształcić wyrażenie na prąd operatorowy w taki sposób, aby doprowadzić je do postaci występującej w tablicy na slajdzie 4. | Przypadek oscylacyjny zmian prądu i napięć w obwodzie szeregowym RLC występuje przy spełnieniu warunku <math>R<2\sqrt{\frac{L}{C}}</math> a więc przy małych wartościach rezystancji R. W tym przypadku oba bieguny są zespolone. Dla wyznaczenia postaci czasowej prądu wygodniej jest zastosować metodę tablic transformat. W tym celu należy przekształcić wyrażenie na prąd operatorowy w taki sposób, aby doprowadzić je do postaci występującej w tablicy na slajdzie 4. | ||
| Linia 529: | Linia 527: | ||
Dla zadanej postaci prądu przekształcenia te są jak następuje | Dla zadanej postaci prądu przekształcenia te są jak następuje | ||
[[Grafika:PEE_M8_Wzor1.jpg]] | : [[Grafika:PEE_M8_Wzor1.jpg]] | ||
Wprowadźmy oznaczenie | Wprowadźmy oznaczenie | ||
| Linia 543: | Linia 541: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd28.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd28.png]] | ||
|valign="top"|Wykorzystując tablicę transformat | |valign="top"|Wykorzystując tablicę transformat możemy uzyskać postać czasową prądu w obwodzie. Można ją zapisać w postaci | ||
: <math>i(t)=\frac{E}{\omega L}e^{-\frac{R}{2L}t}sin(\omega t)</math> | : <math>i(t)=\frac{E}{\omega L}e^{-\frac{R}{2L}t}sin(\omega t)</math> | ||
| Linia 551: | Linia 549: | ||
Wykorzystując podstawowe relacje zachodzące między zmiennymi w obwodzie szeregowym RLC można wyznaczyć pozostałe napięcia w obwodzie w stanie nieustalonym. W przypadku cewki napięcie uzyskuje się przez zróżniczkowanie funkcji opisującej prąd ładowania. | Wykorzystując podstawowe relacje zachodzące między zmiennymi w obwodzie szeregowym RLC można wyznaczyć pozostałe napięcia w obwodzie w stanie nieustalonym. W przypadku cewki napięcie uzyskuje się przez zróżniczkowanie funkcji opisującej prąd ładowania. | ||
<math>u_L(t)=L\frac{di}{dt}=-\frac{E}{\omega \sqrt{LC}}e^{-\frac{R}{2L}t}sin(\omega t-\varphi)</math> | : <math>u_L(t)=L\frac{di}{dt}=-\frac{E}{\omega \sqrt{LC}}e^{-\frac{R}{2L}t}sin(\omega t-\varphi)</math> | ||
gdzie kąt <math>\varphi\,</math> jest określony relacją | gdzie kąt <math>\varphi\,</math> jest określony relacją | ||
| Linia 560: | Linia 558: | ||
<math>u_C(t)=E-u_L(t)-Ri(t)=</math> | <math>u_C(t)=E-u_L(t)-Ri(t)=</math> | ||
: <math>=E-\frac{E}{\omega L}e^{-\frac{R}{2L}t}\left[Rsin(\omega t)-\sqrt{\frac{L}{C}}sin(\omega t-\varphi)\right]</math> | |||
<math>=E-\frac{E}{\omega L}e^{-\frac{R}{2L}t}\left[Rsin(\omega t)-\sqrt{\frac{L}{C}}sin(\omega t-\varphi)\right]</math> | |||
|} | |} | ||
Wersja z 12:00, 25 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
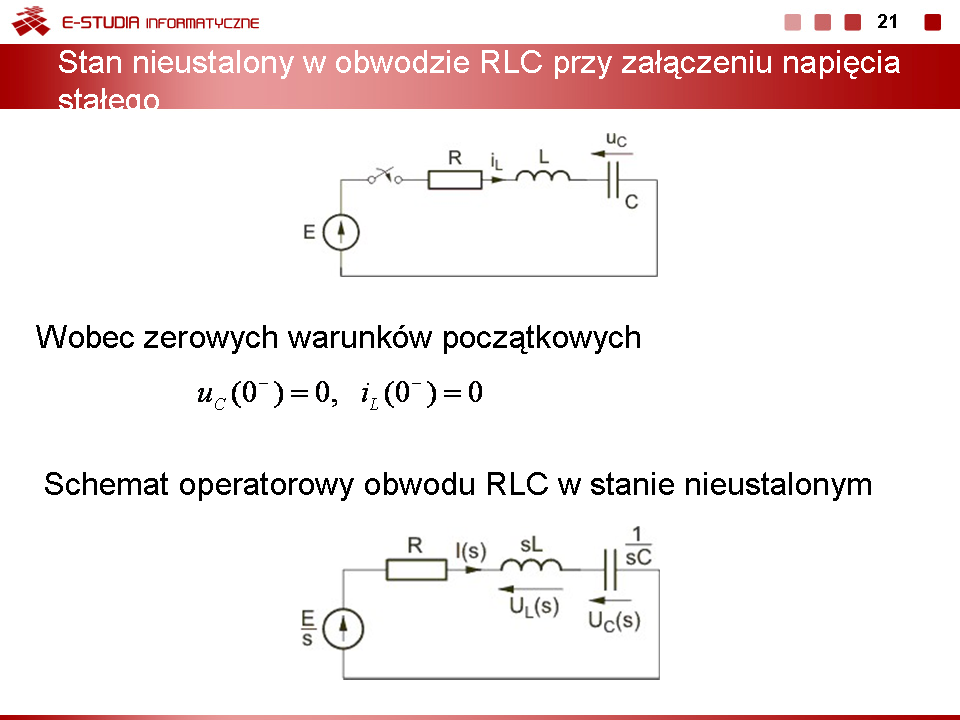
2) Stan ustalony po przełączeniu w obwodzie
|
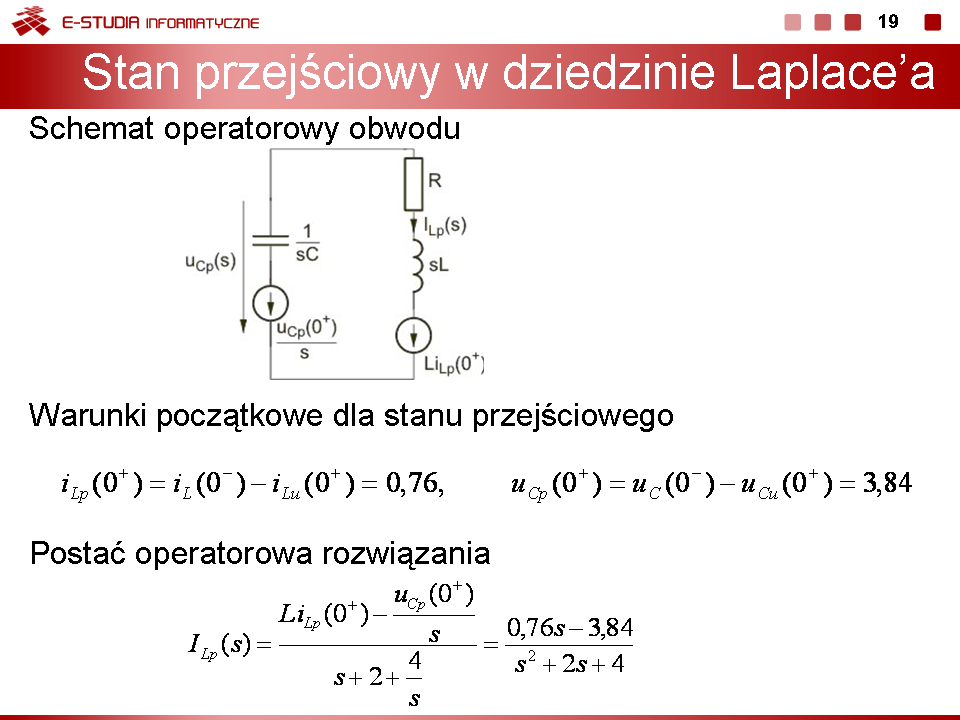
|
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rysunku obok.
Postać operatorowa rozwiązania |

|
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
|

|
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |