PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 181: | Linia 181: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd10.png]] | ||
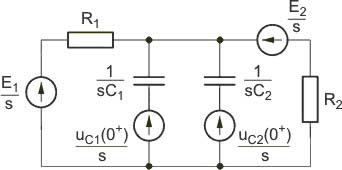
|valign="top"| | |valign="top"|Aby uzyskać bezpośrednie przetworzenie postaci oryginalnej obwodu na obwód w dziedzinie operatorowej Laplace’a należy każdy element obwodu zastąpić odpowiednim modelem w dziedzinie operatorowej. Tutaj podamy te modele dla trzech podstawowych elementów obwodu RLC. | ||
Aby uzyskać bezpośrednie przetworzenie postaci oryginalnej obwodu na obwód w dziedzinie operatorowej Laplace’a należy każdy element obwodu zastąpić odpowiednim modelem w dziedzinie operatorowej. Tutaj podamy te modele dla trzech podstawowych elementów obwodu RLC. | |||
| Linia 202: | Linia 200: | ||
Jak wynika z powyższej zależności impedancja operatorowa dla rezystora jest równa samej rezystancji <math>Z_R(s)=R</math>. Rysunek pierwszy na slajdzie 10 przedstawia model operatorowy rezystora, obowiązujący w dziedzinie zmiennej zespolonej s. | Jak wynika z powyższej zależności impedancja operatorowa dla rezystora jest równa samej rezystancji <math>Z_R(s)=R</math>. Rysunek pierwszy na slajdzie 10 przedstawia model operatorowy rezystora, obowiązujący w dziedzinie zmiennej zespolonej s. | ||
|} | |||
<hr width="100%"> | |||
''Cewka'' | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd10.png]] | |||
|valign="top"|''Cewka'' | |||
Dla uzyskania modelu operatorowego cewki idealnej zastosujemy przekształcenie Laplace’a bezpośrednio do równania opisującego cewkę w dziedzinie czasu | Dla uzyskania modelu operatorowego cewki idealnej zastosujemy przekształcenie Laplace’a bezpośrednio do równania opisującego cewkę w dziedzinie czasu | ||
| Linia 220: | Linia 223: | ||
Jest to połączenie szeregowe impedancji operatorowej odpowiadającej cewce idealnej i źródła napięciowego. Zaciski A-B modelu odpowiadają zaciskom A-B w oryginalnym symbolu cewki. Impedancja <math>Z_L(s)=sL</math> jest impedancją operatorową cewki a <math>Li_L(0^{+})</math> reprezentuje źródło napięcia stanowiące integralną część modelu. | Jest to połączenie szeregowe impedancji operatorowej odpowiadającej cewce idealnej i źródła napięciowego. Zaciski A-B modelu odpowiadają zaciskom A-B w oryginalnym symbolu cewki. Impedancja <math>Z_L(s)=sL</math> jest impedancją operatorową cewki a <math>Li_L(0^{+})</math> reprezentuje źródło napięcia stanowiące integralną część modelu. | ||
|} | |||
<hr width="100%"> | |||
''Kondensator'' | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd10.png]] | |||
|valign="top"|''Kondensator'' | |||
Dla uzyskania modelu operatorowego kondensatora idealnego skorzystamy z jego opisu w dziedzinie czasu | Dla uzyskania modelu operatorowego kondensatora idealnego skorzystamy z jego opisu w dziedzinie czasu | ||
Wersja z 11:39, 25 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
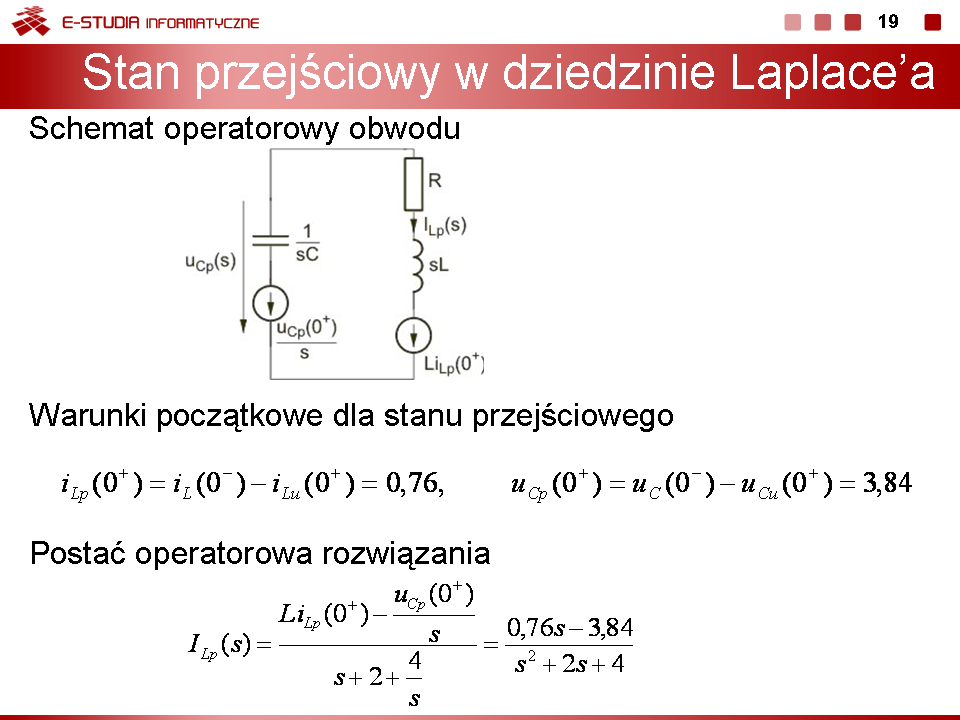
3) Stan przejściowy po przełączeniu
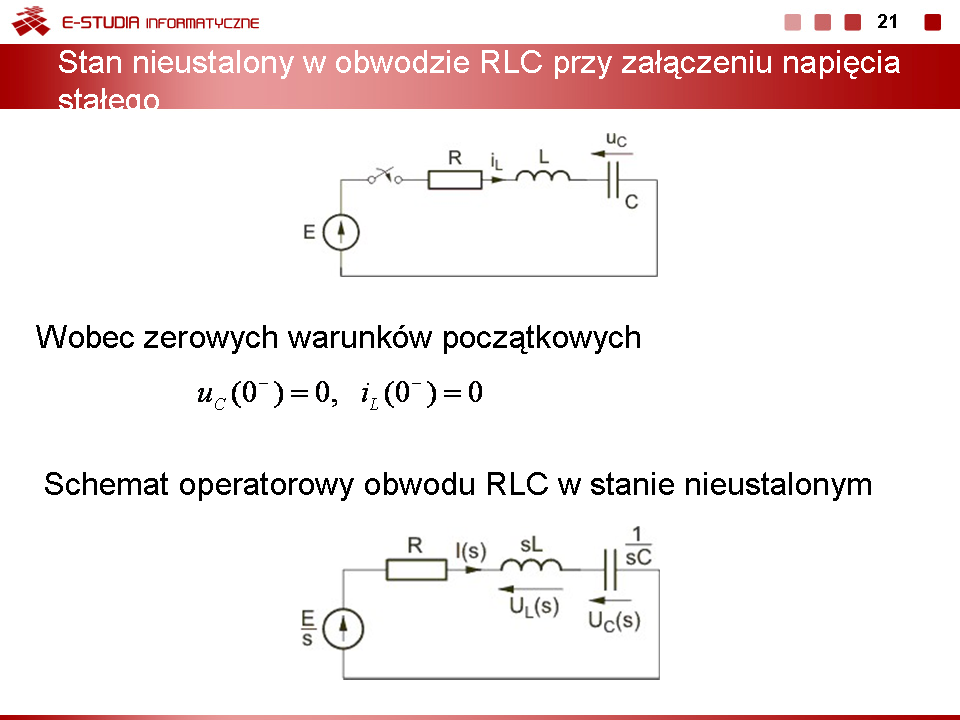
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
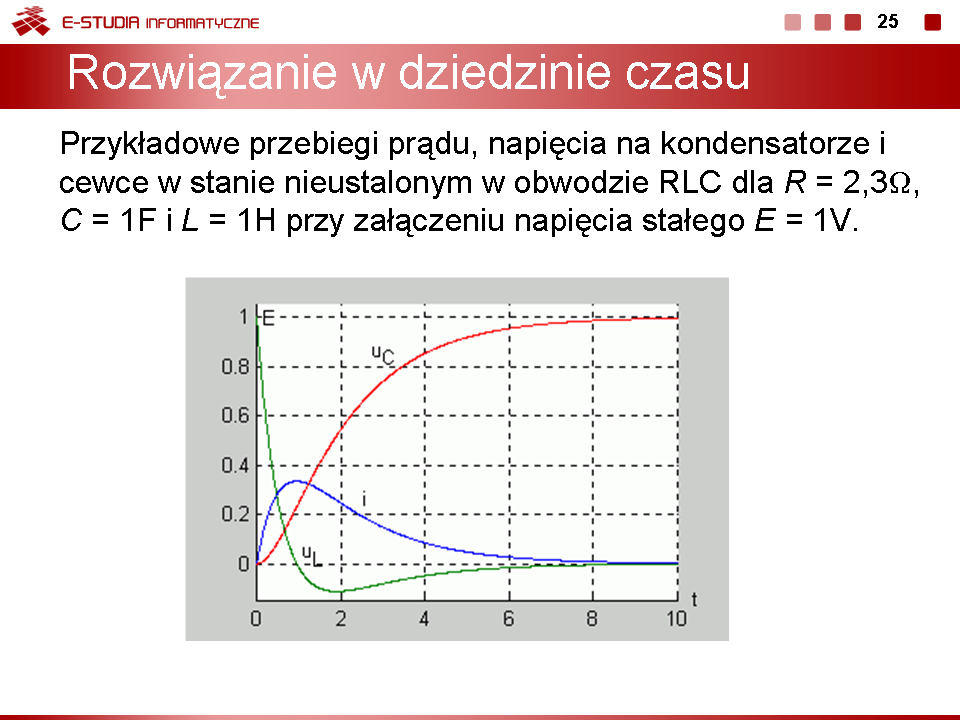
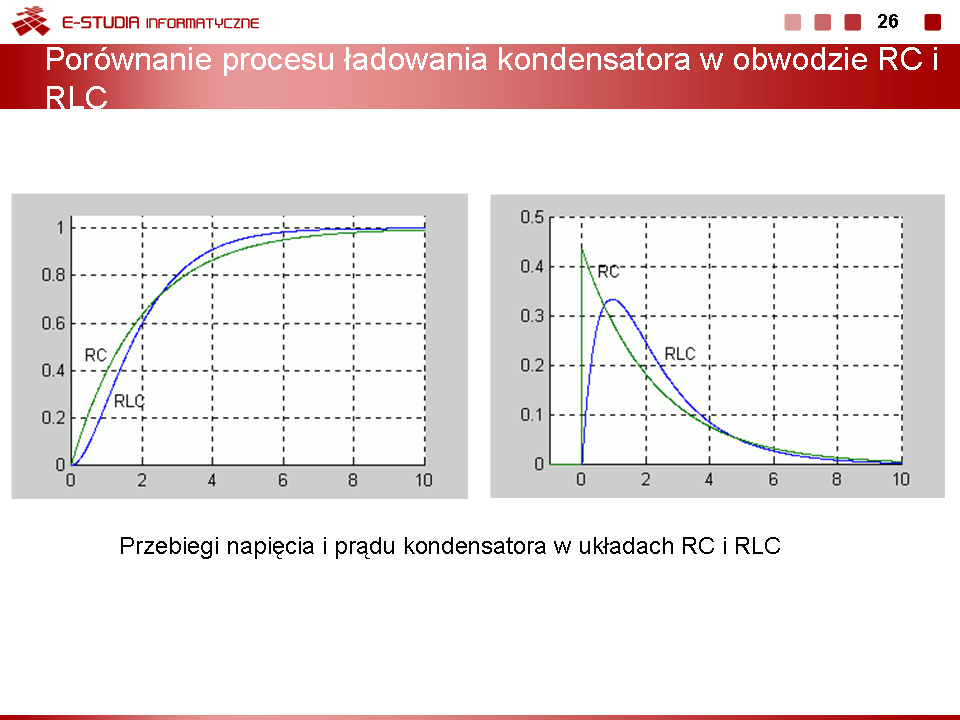
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
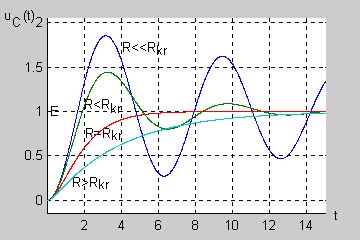
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |