PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 157: | Linia 157: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd9.png]] | ||
|valign="top"| | |valign="top"|Metoda residuów jakkolwiek koncepcyjnie bardzo prosta staje się żmudna, jeśli bieguny układu są zespolone. Jest to szczególnie widoczne przy wysokich stopniach mianownika transmitancji operatorowej. W takich przypadkach zwykle korzystniejsze jest zastosowanie metody wykorzystującej tablice transformat Laplace’a. | ||
Metoda residuów jakkolwiek koncepcyjnie bardzo prosta staje się żmudna, jeśli bieguny układu są zespolone. Jest to szczególnie widoczne przy wysokich stopniach mianownika transmitancji operatorowej. W takich przypadkach zwykle korzystniejsze jest zastosowanie metody wykorzystującej tablice transformat Laplace’a. | |||
Przy korzystaniu z tablic transformat należy poprzez elementarne przekształcenia doprowadzić daną transformatę do postaci standardowej znajdującej się w tablicy transformat (u nas tablica ze slajdu 4) a następnie odczytać z niej oryginał. Jest ona szczególnie wygodna jeśli bieguny układu są zespolone, gdyż w procesie przekształcania transformaty nie występuje potrzeba wyznaczania tych biegunów a wszystkie obliczenia dokonywane są na wartościach rzeczywistych. W praktyce przy stosowaniu tej metody transmitancję wyższych rzędów (n>2) rozkłada się na składniki rzędu drugiego i wszystkie przekształcenia dokonuje na wielomianach rzędu pierwszego lub drugiego. Idę metody wyjaśnimy na przykładach liczbowych. | Przy korzystaniu z tablic transformat należy poprzez elementarne przekształcenia doprowadzić daną transformatę do postaci standardowej znajdującej się w tablicy transformat (u nas tablica ze slajdu 4) a następnie odczytać z niej oryginał. Jest ona szczególnie wygodna jeśli bieguny układu są zespolone, gdyż w procesie przekształcania transformaty nie występuje potrzeba wyznaczania tych biegunów a wszystkie obliczenia dokonywane są na wartościach rzeczywistych. W praktyce przy stosowaniu tej metody transmitancję wyższych rzędów (n>2) rozkłada się na składniki rzędu drugiego i wszystkie przekształcenia dokonuje na wielomianach rzędu pierwszego lub drugiego. Idę metody wyjaśnimy na przykładach liczbowych. | ||
| Linia 167: | Linia 165: | ||
Obliczyć transformatę odwrotną Laplace’a dla funkcji F(s) danej w postaci | Obliczyć transformatę odwrotną Laplace’a dla funkcji F(s) danej w postaci | ||
: <math>F(s)=\frac{1}{s^2+s+1}</math> | : <math>F(s)=\frac{1}{s^2+s+1}</math> | ||
Wobec zespolonych pierwiastków mianownika wykorzystamy tablicę transformat ze slajdu 4. Porównanie postaci danej transformaty z danymi zawartymi w tablicy wskazuje, że należy ją doprowadzić do postaci transformaty odpowiadającej funkcji sinusoidalnej tłumionej wykładniczo (wiersz 6 w tablicy). Kolejność czynności jest tu następująca | Wobec zespolonych pierwiastków mianownika wykorzystamy tablicę transformat ze slajdu 4. Porównanie postaci danej transformaty z danymi zawartymi w tablicy wskazuje, że należy ją doprowadzić do postaci transformaty odpowiadającej funkcji sinusoidalnej tłumionej wykładniczo (wiersz 6 w tablicy). Kolejność czynności jest tu następująca | ||
: <math>F(s)=\sqrt{4/3} \frac{\sqrt{3/4}}{(s+0,5)^2+(\sqrt{3/4})^2}</math> | : <math>F(s)=\sqrt{4/3} \frac{\sqrt{3/4}}{(s+0,5)^2+(\sqrt{3/4})^2}</math> | ||
Porównanie tej postaci z wierszem szóstym tablicy ze slajdu 4 pokazuje, że <math>\alpha=0,5</math>, a <math>\omega=\sqrt{3/4}</math>. Funkcja oryginału jest więc określona wzorem | |||
Porównanie tej postaci z wierszem szóstym tablicy ze slajdu 4 pokazuje, że <math>\alpha=0,5</math> a <math>\omega=\sqrt{3/4}</math>. | |||
Funkcja oryginału jest więc określona wzorem | |||
: <math>f(t)=\sqrt{4/3}e^{-0,5t}sin(\sqrt{3/4}t)</math> | : <math>f(t)=\sqrt{4/3}e^{-0,5t}sin(\sqrt{3/4}t)</math> | ||
Wersja z 11:35, 25 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
3) Stan przejściowy po przełączeniu
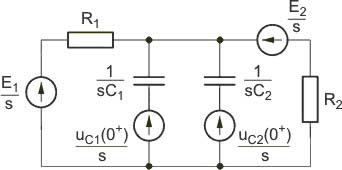
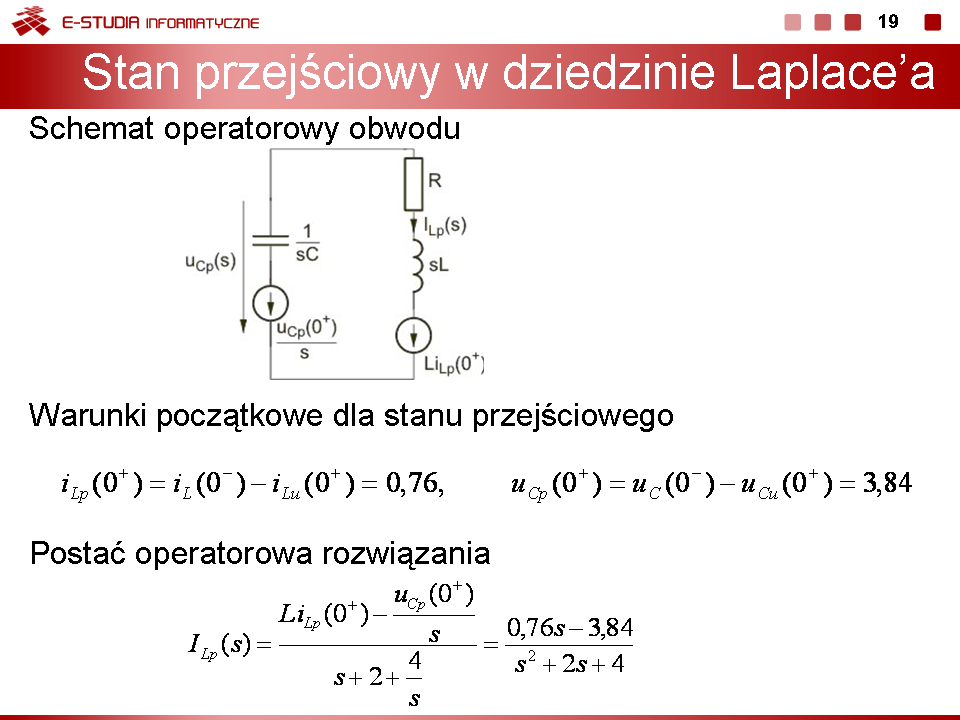
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
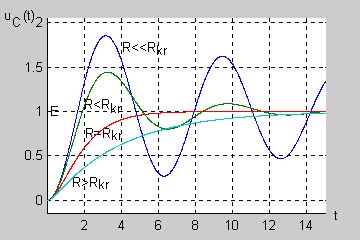
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |