PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 69: | Linia 69: | ||
Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola <math>p|cdot V=R\cdot T</math> przez wartość średniej masy molowej powietrza, określonej z uwzględnieniem procentowej zawartości azotu, tlenu i pozostałych gazów w powietrzu, otrzymujemy | Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola <math>p|cdot V=R\cdot T</math> przez wartość średniej masy molowej powietrza, określonej z uwzględnieniem procentowej zawartości azotu, tlenu i pozostałych gazów w powietrzu, otrzymujemy | ||
<math>p\cdot (V/M)=\frac{R\cdot T}{M}</math> | <math>p\cdot \begin{matrix} \underbrace{ (V/M) } \\ {1/{\rho}} \end{matrix}=\frac{R\cdot T}{M}</math> , czyli <math>\rho=\frac{M\cdot p}{R\cdot T}</math> | ||
Więc możemy napisać, że | |||
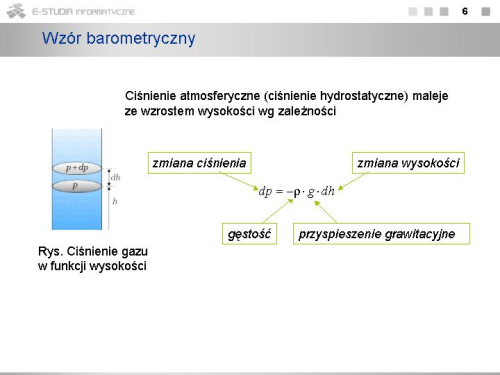
: <math>dp=-\frac{M\cdot p\cdot g}{R\cdot T}\cdot dh</math> | |||
Otrzymujemy w ten sposób równanie różniczkowe o rozdzielonych zmiennych | |||
: <math>\frac{dp}{p}=-\frac{M \cdot g}{R\cdot T}\cdot dh</math> | |||
Zakładając, że temperatura atmosfery ma wartość stałą (tzw. atmosfera izotermiczna) i pole grawitacyjne jest jednorodne <math>(g(h) = const)\,</math> możemy łatwo scałkować to równanie otrzymując | |||
: <math>lnp=-\frac{M \cdot g\cdot h}{R\cdot T}+lnC</math> | |||