PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 40: | Linia 40: | ||
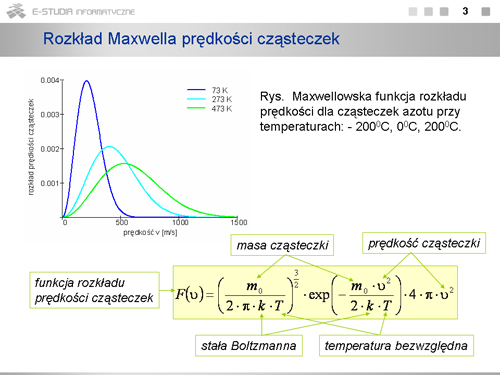
Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
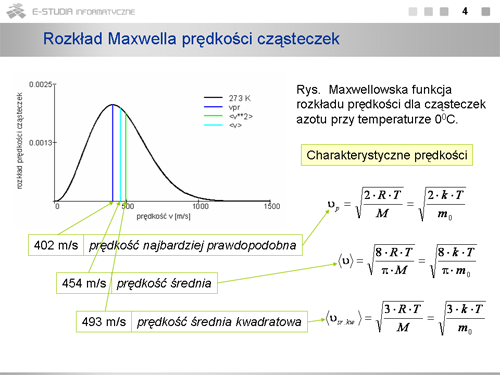
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd4.png]] | |||
|valign="top"|Dla każdej temperatury można określić prędkość, która występuje najczęściej, czyli najwięcej cząsteczek ma prędkości bliskie tej wartości. Wartość ta odpowiada maksimum rozkładu Maxwella. Prędkość tę nazywamy prędkością najbardziej prawdopodobną, <math>v_p\,</math> . Można ją określić z matematycznego warunku na maksimum funkcji. | |||
:<math>\frac{dF(v)}{dv}\Big|_{v=v_p}=0</math> | |||
Stąd otrzymuje się <math>v_p=\sqrt{2\cdot k\cdot T/m_0 }</math> , a więc <math>v_p<v_{śr. kw.}</math> jak to wynika z definicji średniej prędkości kwadratowej (teoria kinetyczna). | |||
Korzystając z funkcji rozkładu można obliczyć odpowiednio prędkość średnią (średnia arytmetyczną wszystkich prędkości) | |||