PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 290: | Linia 290: | ||
Jest to przebieg typu wykładniczego, w którym stan przejściowy trwa tym dłużej im dłuższa jest stała czasowa. Praktycznie po 5 stałych czasowych stan przejściowy w obwodzie zanika przechodząc w stan ustalony. | Jest to przebieg typu wykładniczego, w którym stan przejściowy trwa tym dłużej im dłuższa jest stała czasowa. Praktycznie po 5 stałych czasowych stan przejściowy w obwodzie zanika przechodząc w stan ustalony. | ||
|} | |} | ||
| Linia 313: | Linia 311: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd14.png]] | ||
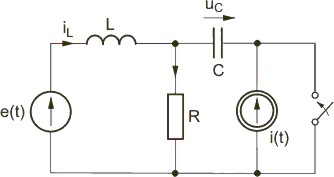
|valign="top"|Wyznaczenie rozwiązania na prąd w stanie nieustalonym w obwodzie RL pozwala na określenie przebiegu czasowego pozostałych wielkości w obwodzie. Korzystając z zależności definicyjnej cewki | |valign="top"|Wyznaczenie rozwiązania na prąd w stanie nieustalonym w obwodzie RL pozwala na określenie przebiegu czasowego pozostałych wielkości w obwodzie. Korzystając z zależności definicyjnej cewki otrzymuje się | ||
<math>u_L(t)=L\frac{di_L(t)}{dt}=Ee^{-\frac{t}{L/R}}</math> | <math>u_L(t)=L\frac{di_L(t)}{dt}=Ee^{-\frac{t}{L/R}}</math> | ||
Przebieg napięcia na cewce w stanie nieustalonym w obwodzie szeregowym RL przedstawiono na rysunku | Przebieg napięcia na cewce w stanie nieustalonym w obwodzie szeregowym RL przedstawiono na rysunku | ||
[[Grafika:PEE_M7_anim_14.gif]] | [[Grafika:PEE_M7_anim_14.gif]] | ||
Napięcie na rezystorze R, jak wynika z prawa Ohma, jest proporcjonalne do prądu | Napięcie na rezystorze R, jak wynika z prawa Ohma, jest proporcjonalne do prądu | ||
<math>u_R(t)=Ri_L(t)=E(1-e^{-\frac{t}{L/R}})</math> | <math>u_R(t)=Ri_L(t)=E(1-e^{-\frac{t}{L/R}})</math> | ||
|} | |} | ||
| Linia 339: | Linia 332: | ||
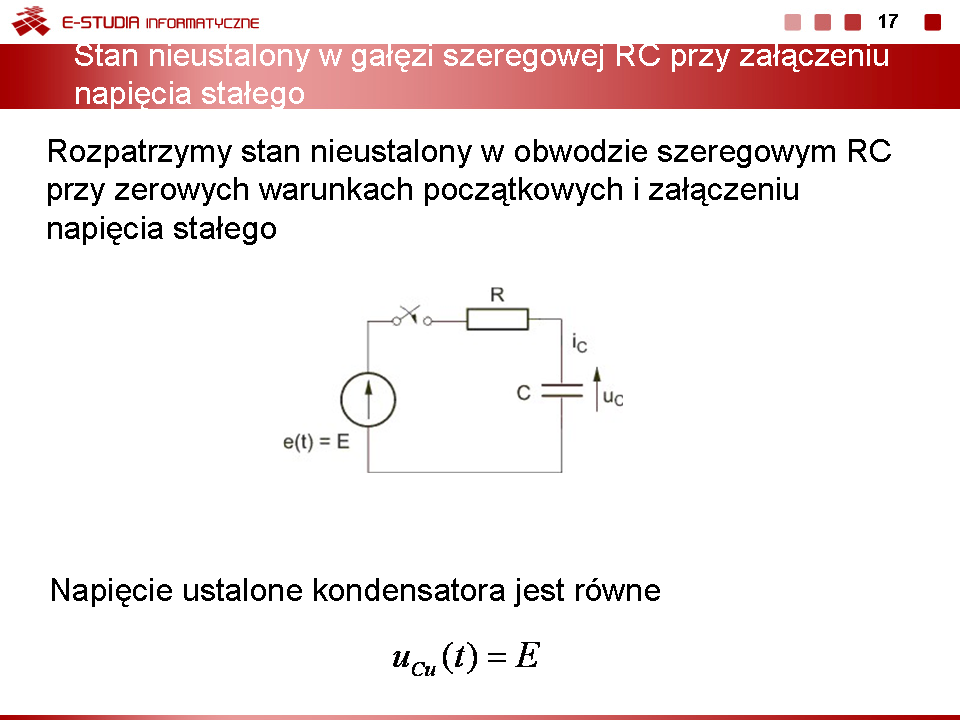
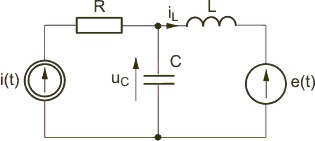
Rozpatrzymy stan nieustalony w obwodzie szeregowym RC przy zerowych warunkach początkowych i załączeniu napięcia stałego | Rozpatrzymy stan nieustalony w obwodzie szeregowym RC przy zerowych warunkach początkowych i załączeniu napięcia stałego | ||
Wobec braku zasilania w obwodzie przed przełączeniem w warunki początkowe obwodu są zerowe, co oznacza, że . | Wobec braku zasilania w obwodzie przed przełączeniem w warunki początkowe obwodu są zerowe, co oznacza, że . | ||
| Linia 346: | Linia 338: | ||
Zgodnie z prawem napięciowym Kirchhoffa napięcie ustalone kondensatora jest równe | Zgodnie z prawem napięciowym Kirchhoffa napięcie ustalone kondensatora jest równe | ||
<math>u_{Cu}(t)=E</math> | <math>u_{Cu}(t)=E</math> | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd16.png]] | ||
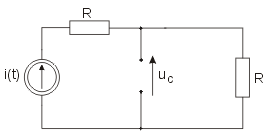
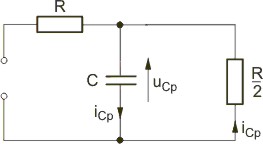
|valign="top"|Schemat obwodu dla stanu przejściowego (po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona) ma postać przedstawioną na rysunku Stosując prawo napięciowe Kirchhoffa dla tego obwodu i uwzględniając, że <math>i_{Cp}=C\frac{du_{Cp}}{dt}</math> , otrzymuje się równanie różniczkowe jednorodne o postaci | |valign="top"|Schemat obwodu dla stanu przejściowego (po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona) ma postać przedstawioną na rysunku Stosując prawo napięciowe Kirchhoffa dla tego obwodu i uwzględniając, że <math>i_{Cp}=C\frac{du_{Cp}}{dt}</math> , otrzymuje się równanie różniczkowe jednorodne o postaci | ||
<math>RC\frac{du_{Cp}}{dt}+u_{Cp}=0</math> | <math>RC\frac{du_{Cp}}{dt}+u_{Cp}=0</math> | ||
Równanie charakterystyczne odpowiadające mu przyjmuje więc postać | Równanie charakterystyczne odpowiadające mu przyjmuje więc postać | ||
<math>RCs+1=0</math> | <math>RCs+1=0</math> | ||
Równanie to posiada jeden pierwiastek <math>s_1=-1/(RC)</math> W związku z powyższym jego rozwiązanie wynikające ze wzoru przyjmie uproszczoną postać | Równanie to posiada jeden pierwiastek <math>s_1=-1/(RC)</math> W związku z powyższym jego rozwiązanie wynikające ze wzoru przyjmie uproszczoną postać | ||
<math>u_{Cp}=A_1e^{s_1t}=A_1e^{-\frac{t}{RC}}</math> | <math>u_{Cp}=A_1e^{s_1t}=A_1e^{-\frac{t}{RC}}</math> | ||
W rozwiązaniu tym współczynnik <math>A_1\,</math> jest stałą całkowania, którą należy wyznaczyć korzystając z prawa komutacji. Rozwiązanie całkowite będące sumą składowej ustalonej i przejściowej przybiera więc postać | W rozwiązaniu tym współczynnik <math>A_1\,</math> jest stałą całkowania, którą należy wyznaczyć korzystając z prawa komutacji. Rozwiązanie całkowite będące sumą składowej ustalonej i przejściowej przybiera więc postać | ||
<math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | <math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd17.png]] | ||
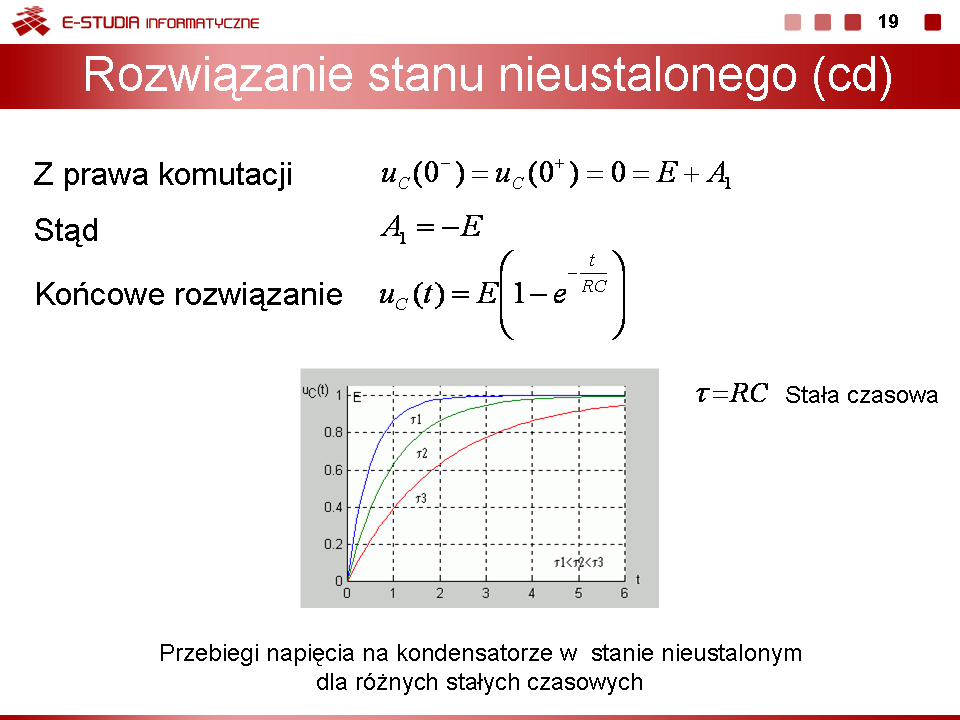
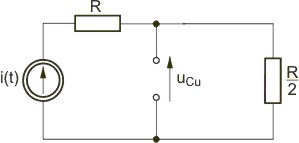
|valign="top"|Z prawa komutacji dla kondensatora wynika, że <math>u_C(0^-)=u_C(0^+)</math> , stąd wobec <math>u_C(0^-)=0</math> otrzymuje się | |valign="top"|Z prawa komutacji dla kondensatora wynika, że <math>u_C(0^-)=u_C(0^+)</math> , stąd wobec <math>u_C(0^-)=0</math> otrzymuje się | ||
<math>0=E+A_1</math> | <math>0=E+A_1</math> | ||
oraz | oraz | ||
<math>A_1=-E</math> | <math>A_1=-E</math> | ||
Rozwiązanie czasowe określające przebieg napięcia na kondensatorze przyjmuje więc postać | Rozwiązanie czasowe określające przebieg napięcia na kondensatorze przyjmuje więc postać | ||
<math>u_C(t)=E(1-e6{-\frac{t}{RC}})</math> | <math>u_C(t)=E(1-e6{-\frac{t}{RC}})</math> | ||
Wprowadzając pojęcie stałej czasowej obwodu RC jako iloczynu rezystancji R i pojemności C | Wprowadzając pojęcie stałej czasowej obwodu RC jako iloczynu rezystancji R i pojemności C | ||
<math>\tau=RC</math> | <math>\tau=RC</math> | ||
rozwiązanie na napięcie kondensatora w stanie nieustalonym można zapisać w postaci | rozwiązanie na napięcie kondensatora w stanie nieustalonym można zapisać w postaci | ||
<math>u_C(t)=E(1-e^{-\frac{t}{\tau}})</math> | <math>u_C(t)=E(1-e^{-\frac{t}{\tau}})</math> | ||
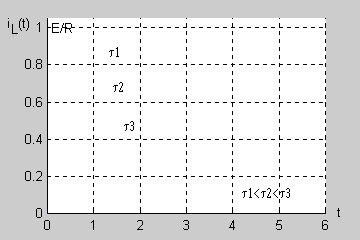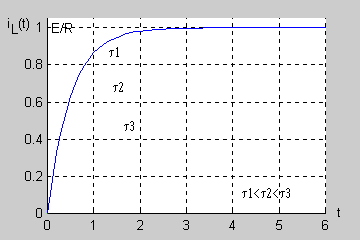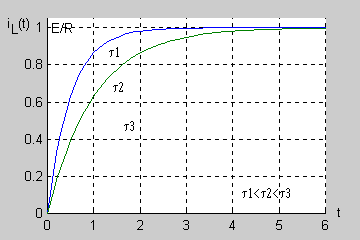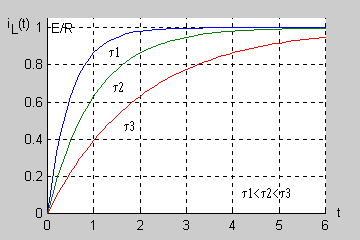
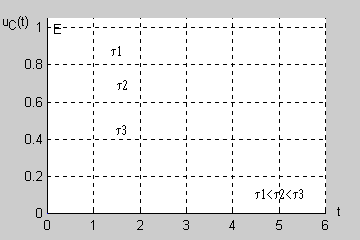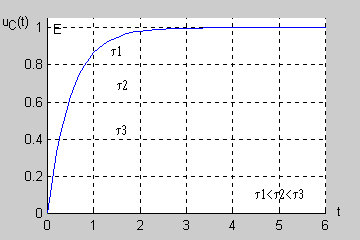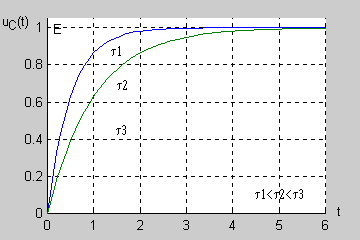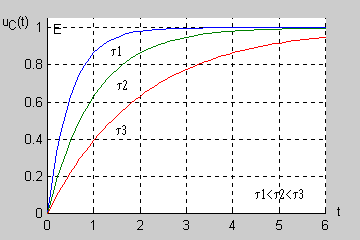
Jak łatwo sprawdzić podstawową jednostką stałej czasowej w obwodzie RC jest również sekunda (jednostką rezystancji jest <math>1\Omega = 1V/A</math>, a jednostką pojemności jest <math>1F = 1As/V</math>). Na rysunku przedstawiono przebiegi napięcia na kondensatorze w stanie nieustalonym <math>u_C(t)=E(1-e^{-\frac{t}{\tau}})</math> dla różnych wartości stałej czasowej. | Jak łatwo sprawdzić podstawową jednostką stałej czasowej w obwodzie RC jest również sekunda (jednostką rezystancji jest <math>1\Omega = 1V/A</math>, a jednostką pojemności jest <math>1F = 1As/V</math>). Na rysunku przedstawiono przebiegi napięcia na kondensatorze w stanie nieustalonym <math>u_C(t)=E(1-e^{-\frac{t}{\tau}})</math> dla różnych wartości stałej czasowej. | ||
[[Grafika:PEE_M7_anim_17.gif]] | [[Grafika:PEE_M7_anim_17.gif]] | ||
Im dłuższa stała czasowa tym dłużej trwa stan przejściowy w obwodzie (zanikanie zmian napięcia do zera). | Im dłuższa stała czasowa tym dłużej trwa stan przejściowy w obwodzie (zanikanie zmian napięcia do zera). | ||
| Linia 425: | Linia 396: | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
Wersja z 13:46, 24 sie 2006

|
Metoda równań różniczkowych w rozwiązaniu stanu nieustalonego w obwodach elektrycznych |
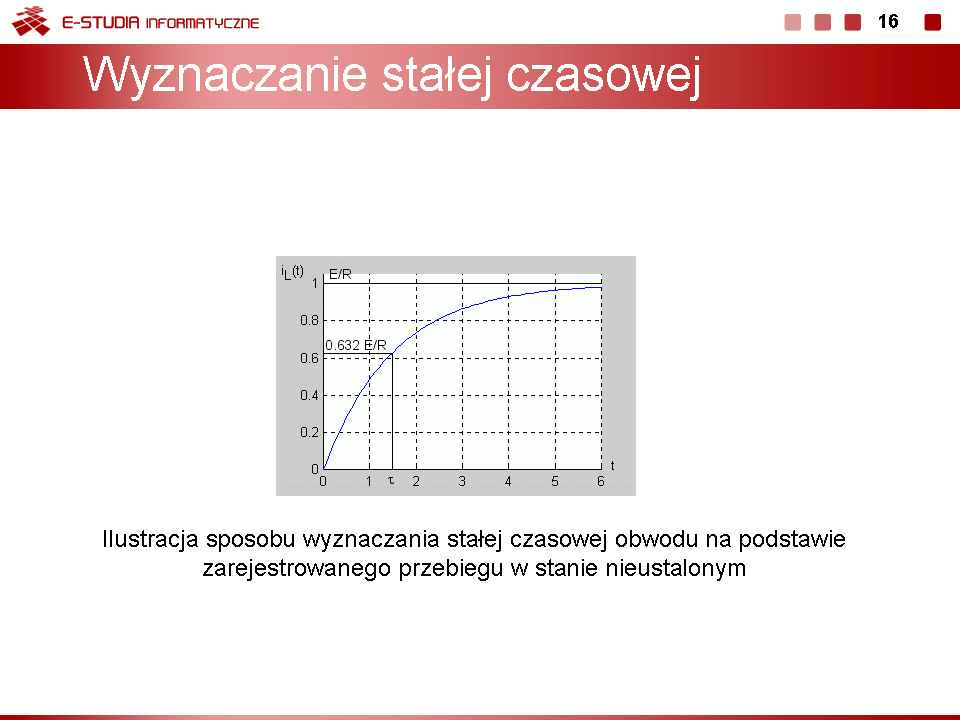
| Łatwo wykazać, że po upływie 3 stałych czasowych ( ) napięcie uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony.
Stałą czasową można wyznaczyć bezpośrednio na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i pojemności, podobnie jak to miało miejsce w przypadku obwodu RL. |
| Zadania sprawdzające
Zadanie 7.1 Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: Rozwiązanie Warunki początkowe dotyczą stanu ustalonego przed przełączeniem, w którym w obwodzie działają oba źródła wymuszające. Stosując metodę symboliczną analizy obwodu otrzymujemy
|

|
Równania obwodu w stanie ustalonym
Warunki początkowe:
|
| Zadanie 7.2
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku Rozwiązanie Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
Rozwiązanie Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
Schemat obwodu w stanie ustalonym po przełączeniu
Schemat obwodu w stanie przejściowym po przełączeniu
Postać ostateczna rozwiązania:
|