PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 156: | Linia 156: | ||
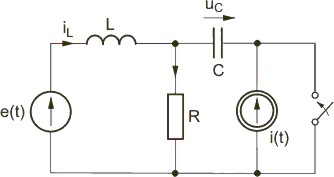
<math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | <math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | ||
Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu A jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz B zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu A o postaci | Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu <math>\mathbf{A}</math> jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz <math>\mathbf{B}</math> zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu <math>\mathbf{A}</math> o postaci | ||
<math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | <math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | ||
| Linia 174: | Linia 174: | ||
Rozwiązanie powyższego równania różniczkowego, podobnie jak w metodzie zmiennych stanu, można przedstawić w postaci sumy dwu składowych: ustalonej <math>x_u(t)</math> wymuszonej przez źródło oraz składowej przejściowej <math>x_p(t)</math> , zwanej również składową swobodną, pochodzącą od niezerowych warunków początkowych dla tej składowej. | Rozwiązanie powyższego równania różniczkowego, podobnie jak w metodzie zmiennych stanu, można przedstawić w postaci sumy dwu składowych: ustalonej <math>x_u(t)</math> wymuszonej przez źródło oraz składowej przejściowej <math>x_p(t)</math> , zwanej również składową swobodną, pochodzącą od niezerowych warunków początkowych dla tej składowej. | ||
'''Składowa wymuszona''' stanowi rozwiązanie ustalone obwodu po komutacji i może być wyznaczona metodą symboliczną. '''Składowa przejściowa''' charakteryzuje fizycznie procesy zachodzące w obwodzie elektrycznym na skutek niezerowych warunków początkowych przy braku wymuszeń zewnętrznych. Odpowiada ona obwodowi, w którym wyeliminowano wszystkie zewnętrzne źródła wymuszające (źródła napięciowe zwarte a prądowe rozwarte). | '''Składowa wymuszona''' stanowi rozwiązanie ustalone obwodu po komutacji i może być wyznaczona metodą symboliczną. '''Składowa przejściowa''' charakteryzuje fizycznie procesy zachodzące w obwodzie elektrycznym na skutek niezerowych warunków początkowych przy braku wymuszeń zewnętrznych <math>f(t)=0</math>. Odpowiada ona obwodowi, w którym wyeliminowano wszystkie zewnętrzne źródła wymuszające (źródła napięciowe zwarte a prądowe rozwarte). | ||
|} | |} | ||
| Linia 183: | Linia 182: | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd9.png]] | ||
|valign="top"|Składowa przejściowa zależy jedynie od warunków początkowych odniesionych do tej składowej (napięć początkowych kondensatorów i prądów początkowych cewek), struktury obwodu i wartości parametrów tego obwodu. Dla obwodów elektrycznych zawierających elementy rozpraszające energię (rezystancje) składowa przejściowa, jak zostanie pokazane później, zanika z biegiem czasu do zera. Równanie składowej przejściowej otrzymuje się zakładając wymuszenie <math>f(t)\,</math> we wzorze równe zeru i zastępując zmienną <math>x(t)\,</math> poprzez jej składową przejściową <math>x_p(t)\,</math> . Otrzymuje się wówczas równanie różniczkowe jednorodne o postaci | |valign="top"|Składowa przejściowa zależy jedynie od warunków początkowych odniesionych do tej składowej (napięć początkowych kondensatorów i prądów początkowych cewek), struktury obwodu i wartości parametrów tego obwodu. Dla obwodów elektrycznych zawierających elementy rozpraszające energię (rezystancje) składowa przejściowa, jak zostanie pokazane później, zanika z biegiem czasu do zera. Równanie składowej przejściowej otrzymuje się zakładając wymuszenie <math>f(t)\,</math> we wzorze równe zeru i zastępując zmienną <math>x(t)\,</math> poprzez jej składową przejściową <math>x_p(t)\,</math> . Otrzymuje się wówczas równanie różniczkowe jednorodne o postaci | ||
<math>a_n\frac{d^nx_p}{dt^n}+a_{n-1}\frac{d^{n-1}x_p}{dt^{n-1}}+a_{n-2}\frac{d^{n-2}x_p}{dt^{n-2}}+...+a_1\frac{dx_p}{dt}+a_0x_p=0</math> | <math>a_n\frac{d^nx_p}{dt^n}+a_{n-1}\frac{d^{n-1}x_p}{dt^{n-1}}+a_{n-2}\frac{d^{n-2}x_p}{dt^{n-2}}+...+a_1\frac{dx_p}{dt}+a_0x_p=0</math> | ||
| Linia 189: | Linia 187: | ||
Rozwiązanie powyższego równania jednorodnego uzyskuje się za pośrednictwem równania charakterystycznego | Rozwiązanie powyższego równania jednorodnego uzyskuje się za pośrednictwem równania charakterystycznego | ||
<math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s+a+a_0=0</math> | <math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s+a+a_0=0</math> | ||
| Linia 203: | Linia 200: | ||
|valign="top"|W tym punkcie ograniczymy się jedynie do przypadku biegunów pojedynczych. Przy takim założeniu rozwiązanie równania dla składowej przejściowej zapiszemy w postaci | |valign="top"|W tym punkcie ograniczymy się jedynie do przypadku biegunów pojedynczych. Przy takim założeniu rozwiązanie równania dla składowej przejściowej zapiszemy w postaci | ||
<math>x_p(t)=\Sigma_{i=1}^n A_i e^{s_it}</math> | |||
<math>x_p(t)=\Sigma_{i=1}^ | |||
W rozwiązaniu tym współczynniki <math>A_i\,</math> są stałymi całkowania, które należy wyznaczyć wykorzystując znajomość warunków początkowych w obwodzie (napięć kondensatorów i prądów cewek w chwili komutacji <math>t=0\,</math>). Z ciągłości prądów cewek i napięć kondensatorów wynika następująca zależność | W rozwiązaniu tym współczynniki <math>A_i\,</math> są stałymi całkowania, które należy wyznaczyć wykorzystując znajomość warunków początkowych w obwodzie (napięć kondensatorów i prądów cewek w chwili komutacji <math>t=0\,</math>). Z ciągłości prądów cewek i napięć kondensatorów wynika następująca zależność | ||
<math>x(0^-)=x(0^+)</math> | |||
<math>x(0^-)= | |||
Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\,</math> i podstawia do wzoru ogólnego . Po wyznaczeniu rozwiązania obwodu dla składowej ustalonej i przejściowej rozwiązanie całkowite jest sumą obu rozwiązań cząstkowych, to znaczy | Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\,</math> i podstawia do wzoru ogólnego . Po wyznaczeniu rozwiązania obwodu dla składowej ustalonej i przejściowej rozwiązanie całkowite jest sumą obu rozwiązań cząstkowych, to znaczy | ||
<math>x(t)=x_u(t)+x_p(t)</math> | <math>x(t)=x_u(t)+x_p(t)</math> | ||
Wersja z 13:34, 24 sie 2006

|
Metoda równań różniczkowych w rozwiązaniu stanu nieustalonego w obwodach elektrycznych |
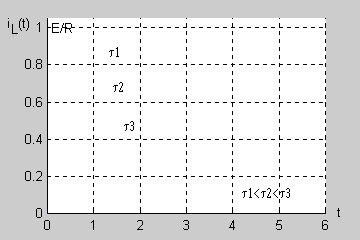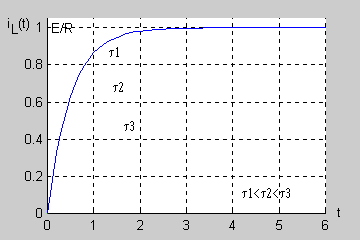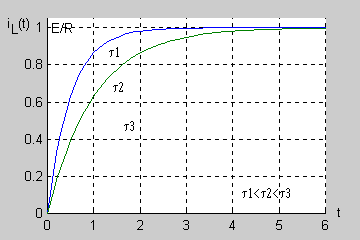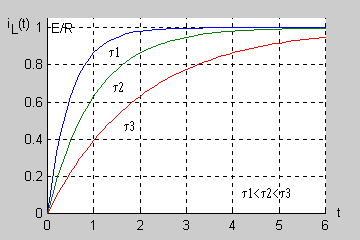
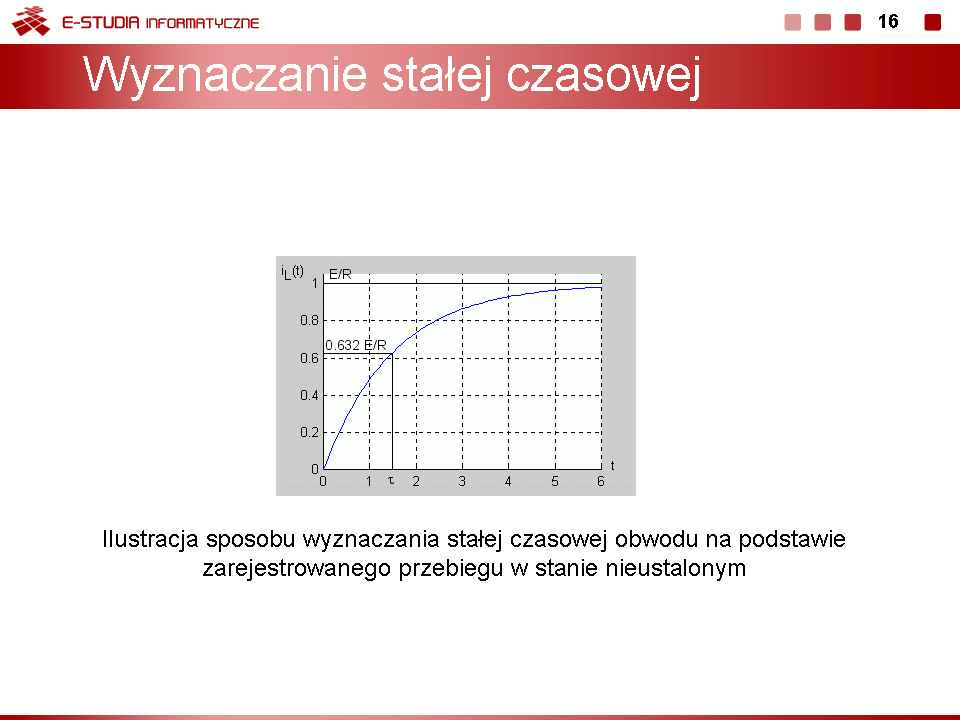
| Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość
|
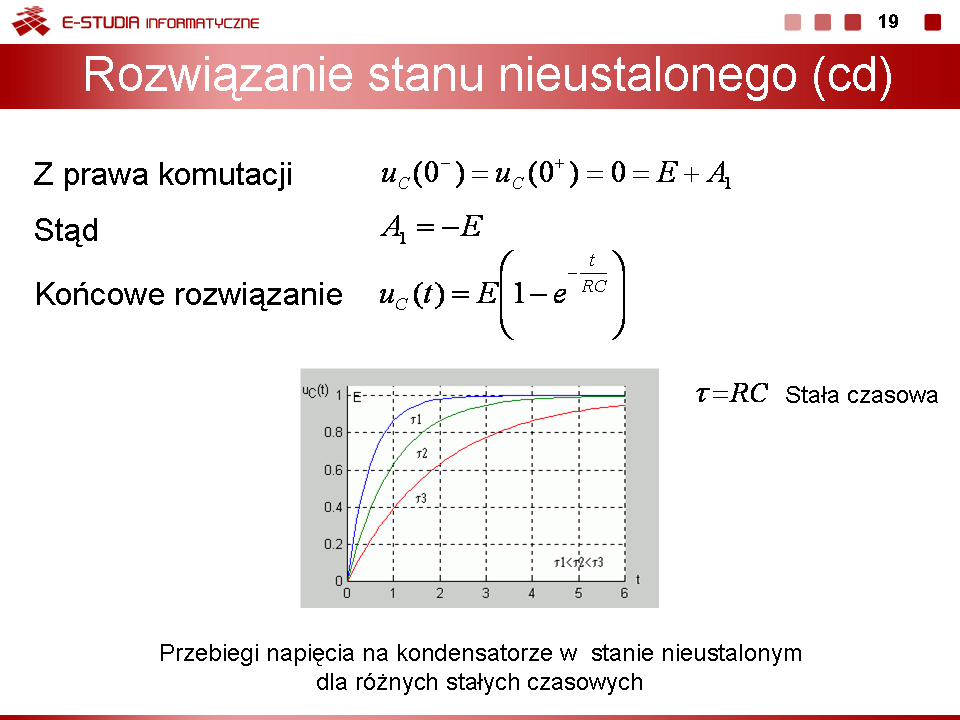
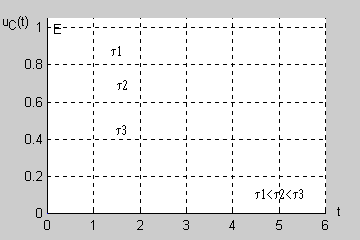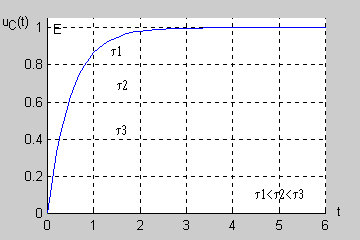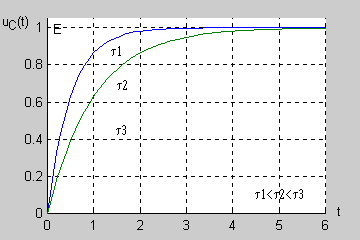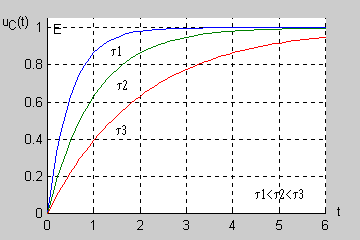
| Łatwo wykazać, że po upływie 3 stałych czasowych ( ) napięcie uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony.
Stałą czasową można wyznaczyć bezpośrednio na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i pojemności, podobnie jak to miało miejsce w przypadku obwodu RL. |
| Zadania sprawdzające
Zadanie 7.1 Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: Rozwiązanie Warunki początkowe dotyczą stanu ustalonego przed przełączeniem, w którym w obwodzie działają oba źródła wymuszające. Stosując metodę symboliczną analizy obwodu otrzymujemy
|

|
Równania obwodu w stanie ustalonym
Warunki początkowe:
|
| Zadanie 7.2
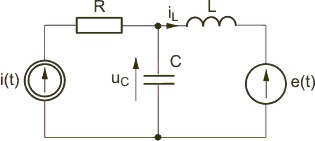
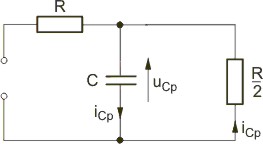
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku Rozwiązanie Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
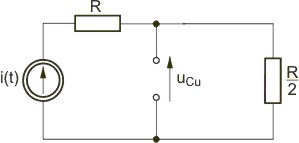
Rozwiązanie Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
Schemat obwodu w stanie ustalonym po przełączeniu
Schemat obwodu w stanie przejściowym po przełączeniu
Postać ostateczna rozwiązania:
|