PEE Moduł 7

Metoda równań różniczkowych w rozwiązaniu stanu nieustalonego w obwodach elektrycznych

---

Podstawowe pojęcia stanów nieustalonych Analizując przebiegi czasowe procesów zachodzących w obwodach elektrycznych należy wyróżnić dwa stany: stan ustalony charakteryzujący się tym, że postać odpowiedzi jest identyczna z postacią wymuszenia (na przykład w odpowiedzi na wymuszenie sinusoidalne odpowiedź ustalona jest również sinusoidalna o tej samej częstotliwości choć innej fazie początkowej i innej amplitudzie) stan nieustalony, w którym przebiegi czasowe odpowiedzi mają inny charakter niż wymuszenie (na przykład w odpowiedzi na wymuszenie stałe odpowiedź obwodu jest wykładniczo malejąca czy oscylacyjna). Stan nieustalony w obwodzie RLC powstaje jako nałożenie się stanu przejściowego (zwykle zanikającego) i stanu ustalonego przy zmianie stanu obwodu spowodowanego przełączeniem. Może on wystąpić w wyniku przełączeń w samym obwodzie pasywnym (zmiana wartości elementów, zwarcie elementu, wyłączenie elementu) lub w wyniku zmiany sygnałów wymuszających (parametrów źródeł napięciowych i prądowych, w tym także załączeniem lub wyłączeniem źródła). Dowolną zmianę w obwodzie nazywać będziemy komutacją. Zakładać będziemy, że czas trwania komutacji jest równy zeru, co znaczy że wszystkie przełączenia odbywają się bezzwłocznie. W obwodach elektrycznych proces komutacji modeluje się zwykle przy pomocy wyłączników i przełączników wskazujących na rodzaj przełączenia. Chwilę czasową poprzedzającą bezpośrednio komutację oznaczać będziemy w ogólności przez (w szczególności przez ), natomiast chwilę bezpośrednio następującą po komutacji przez (w szczególności przez ), gdzie jest chwilą przełączenia (komutacji).

---

Prawa komutacji Z podstawowych praw rządzących obwodami elektrycznymi wynika, że w rezultacie przełączenia zachowana zostaje ciągłość sumy ładunków kondensatorów dołączonych do węzła. Oznacza to, że suma ładunków kondensatorów dołączonych do takiego węzła przed przełączeniem jest równa sumie ładunków kondensatorów dołączonych do tych węzłów po przełączeniu. Zasada ta wynika stąd, że do danego węzła nie może dopłynąć skończony ładunek w zerowym czasie. Podobnie ciągłość zachowuje suma strumieni skojarzonych cewek należących do danego oczka. Suma strumieni skojarzonych cewek należących do oczka przed przełączeniem jest równa sumie strumieni skojarzonych cewek należących do tego oczka po przełączeniu. Prawo komutacji dotyczące kondensatorów Suma ładunków kondensatorów dołączonych do danego węzła nie może zmienić się w sposób skokowy na skutek komutacji, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili $t_0=0$) ${\mathrm{\Sigma }}_i{q}_i(0^{-})={\mathrm{\Sigma }}_i{q}_i(0^{+})$ Jeśli w wyniku przełączenia nie powstają oczka złożone z samych kondensatorów oraz idealnych źródeł napięcia to biorąc pod uwagę zależność $q_C=C{u}_C$ prawo komutacji dla kondensatorów można zapisać w uproszczonej postaci uzależnionej od napięć tych kondensatorów $u_C(0^{-})=u_C(0^{+})$ Ostatnia postać prawa komutacji dotycząca napięcia na kondensatorze jest najczęściej używana w praktyce. Prawo komutacji dotyczące cewek Suma strumieni skojarzonych cewek należących do danego oczka nie może ulec skokowej zmianie na skutek przełączenia w obwodzie, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili $t_0=0$) ${\mathrm{\Sigma }}_i{\psi }_i(0^{-})={\mathrm{\Sigma }}_i{\psi }_i(0^{+})$ Jeśli w wyniku przełączenia nie powstają węzły (dokładniej rozcięcia [5]) do których dołączone są wyłącznie same cewki i źródła prądowe to biorąc pod uwagę, że $\psi =L{i}_L$ prawo ciągłości strumieni może być uproszczone do ciągłości prądu cewek, co zapiszemy w postaci $i_L(0^{-})=i_L(0^{+})$ Jest to najczęściej w praktyce używana postać pierwszego prawa komutacji w odniesieniu do cewki.

---

Przy założeniu, że chwilę komutacji uważać będziemy za chwilę początkową analizy obwodu w stanie nieustalonym $(t_0=0)$ istotnym problemem w analizie obwodu jest wyznaczenie warunków początkowych procesu, czyli wartości napięć na kondensatorach i prądów cewek w chwili przełączenia (u nas $i_L(0^{-})$ oraz $u_C(0^{-})$ ). Zwykle przyjmuje się, że przełączenie następuje ze stanu ustalonego obwodu. Warunki początkowe wynikają wówczas z wartości ustalonych tych wielkości w chwili tuż przed przełączeniem $(t_0=0^{-})$ . Warunki początkowe mogą być przy tym zerowe, jeśli prądy wszystkich cewek i napięcia wszystkich kondensatorów w chwili przełączenia miały wartości zerowe. Znajomość warunków początkowych w obwodzie jest niezbędna przy wyznaczaniu rozwiązania obwodu w stanie nieustalonym. Wyznaczenie stanu początkowego napięcia kondensatora i prądu cewki w obwodzie sprowadza się do rozwiązania stanu ustalonego obwodu przed przełączeniem (przy wymuszeniach sinusoidalnych metodą symboliczną), określenia postaci czasowej tego rozwiązania dla prądu cewki $i_L(t)$ i napięcia kondensatora $u_C(t)$ oraz wyznaczenia wartości tego rozwiązania odpowiadającego chwili czasowej przełączenia (u nas $i_L(0^{-})$ oraz $u_C(0^{-})$ ).

---

Opis obwodu elektrycznego za pomocą równań stanu Wykorzystując opis ogólny elementów RLC oraz prawa Kirchhoffa łatwo pokazać, że liniowe obwody elektryczne RLC w stanach nieustalonych mogą być opisane przez równania różniczkowe i całkowe. Porządkując te równania i eliminując zmienne nie będące prądami cewek i napięciami kondensatorów można uzyskać tak zwaną postać kanoniczną opisu w postaci układu równań różniczkowych, który można przedstawić następująco $\frac{d{x}_1}{dt}=a_1{}_1{x}_1+a_1{}_2+...+a_1{}_n{x}_n{f}_1(t)$ $\frac{d{x}_2}{dt}=a_2{}_1{x}_1+a_2{}_2+...+a_2{}_n{x}_n{f}_2(t)$ $\cdots$ $\frac{d{x}_n}{dt}=a_n{}_1{x}_1+a_n{}_2+...+a_n{}_n{x}_n{f}_n(t)$ Zmienne $x_1,x_2,\cdots ,x_n$ występujące w równaniach oznaczają prądy cewek lub napięcia kondensatorów (tzw. zmienne stanu). W opisie obwodu operuje się zwykle minimalnym zbiorem zmiennych stanu, które są niezbędne dla wyznaczenia pozostałych wielkości w obwodzie. Liczba zmiennych stanu n zależy od liczby reaktancji w obwodzie i jest najczęściej równa (w szczególnych przypadkach mniejsza) sumie liczby kondensatorów i cewek włączonych w obwodzie. Stałe współczynniki $a_i{}_j$ występujące w równaniu (7.5) stanowią kombinacje wartości parametrów R, L, C, M elementów pasywnych obwodu oraz parametrów źródeł sterowanych. Funkcje czasu $f_1(t),f_2(t),...,f_n(t)$ związane są z wymuszeniami napięciowymi i prądowymi w obwodzie.

---

W przypadku obwodów liniowych funkcje fi(t) występujące po prawej stronie wzoru są liniowymi funkcjami wymuszeń prądowych i napięciowych. Oznaczając wymuszenia prądowe bądź napięciowe w ogólności przez $u_i(i=1,2,...,m)$ można opis stanowy obwodu przedstawić w postaci $\frac{dx(t)}{dt}=Ax(t)+Bu(t)$ gdzie $A$ jest macierzą stanu o wymiarach Parser nie mógł rozpoznać (błąd składni): {\displaystyle n×n\,} zawierającą elementy $a_i{}_j$ , a macierz $B$ o wymiarach Parser nie mógł rozpoznać (błąd składni): {\displaystyle n×m\,} składa się ze współczynników uzależniających pochodną zmiennych stanu od wektora wymuszeń $u$. Jest to ogólna postać opisu stanowego obwodu liniowego RLC. Reprezentuje ona układ n równań różniczkowych liniowych rzędu pierwszego. Elementy macierzy A i B zależą wyłącznie od wartości parametrów obwodu. Elementy wektora u stanowią źródła niezależne prądu i napięcia w obwodzie. Zmienne stanu to niezależne napięcia na kondensatorach i prądy cewek. Równanie nazywane jest macierzowym równaniem stanu obwodu elektrycznego. Rozwiązanie tego równania pozwala wyznaczyć przebiegi czasowe zmiennych stanu tworzących wektor $x(t)$. Jeśli dodatkowo interesują nas inne zmienne w obwodzie, na przykład prądy i napięcia rezystorów, prądy kondensatorów czy napięcia na cewkach to należy sformułować drugie równanie, tzw. równanie odpowiedzi $y(t)$, które uzależnia poszukiwane wielkości od zmiennych stanu i wymuszeń. Równanie to zapiszemy w postaci $y(t)=Cx(t)+Du(t)$ Równania tworzą parę równań stanu $\frac{dx(t)}{dt}=Ax(t)+Bu(t)$ $y(t)=Cx(t)+Du(t)$ Równania tworzą parę równań stanu $\frac{dx(t)}{dt}=Ax(t)+Bu(t)$ $y(t)=Cx(t)+Du(t)$ która w pełni opisuje stan obwodu przy założeniu, że znane są warunki początkowe $x_0=x(t0)$, gdzie $t_0$ oznacza chwilę przełączenia. W przypadku ogólnym rozwiązanie równania stanu przyjmuje postać $x(t)=e^{A(t-t_0)}x(t_0)+\underset{t}{\int }0t{e}^{A(t-\tau )}Bu(\tau )d\tau$ Zależność powyższa stanowi rozwiązanie ogólne, które dla konkretnych wartości funkcji wymuszających zadanych wektorem u wyznacza rozwiązanie czasowe dla zmiennych stanu. We współczesnych metodach numerycznych równania stanu stanowią punkt wyjścia w określaniu dokładnego rozwiązania równań liniowych lub przybliżonego dla zlinearyzowanych równań stanu. Są one również bardzo wygodne w zastosowaniach przybliżonych metod całkowania równań różniczkowych ze względu na to, że wszystkie równania stanu są rzędu pierwszego, dla których istnieją wyspecjalizowane metody całkowania przybliżonego. W rozwiązaniu (7.11) równania stanu występują dwa człony, z których pierwszy jest zależny tylko od warunków początkowych niezerowych (energii zgromadzonej w cewkach i kondensatorach), a drugi stanowi odpowiedź obwodu na wymuszenia tworzące wektor $u(t)$. Pierwszą część utożsamiać będziemy wyłącznie ze składową przejściową pochodzącą od niezerowych warunków początkowych, a drugą – z odpowiedzią obwodu na wymuszenie. Odpowiedź druga zawiera składowe ustaloną jak i część składowej przejściowej.

---

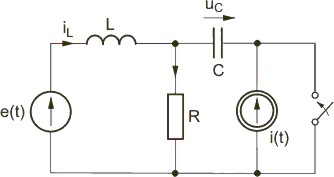
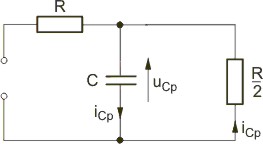
Przykład Napisać układ równań stanu dla obwodu elektrycznego przedstawionego na rysunku

---

Rozwiązanie Z praw Kirchhoffa napisanych dla obwodu z rysunku wynikają następujące równania $e=R{i}_C+u_C+u_L$ $i=i_L=L-i_C$ Biorąc pod uwagę, że $u_L=L\frac{d{i}_L}{dt}$ oraz $i_C=C\frac{d{u}_C}{dt}$ równania Kirchhoffa można przekształcić do równoważnej postaci równań różniczkowych $e=R(i_L-i)+L\frac{d{i}_L}{dt}+U_C$ $C\frac{d{u}_C}{dt}=i_L-i$ które przyjmują uporządkowaną formę odpowiadającą postaci $\frac{d{i}_L}{dt}=-\frac{R}{L}{i}_L-\frac{1}{L}{u}_C+\frac{1}{L}e+\frac{R}{L}i$ $\frac{d{u}_C}{dt}=\frac{1}{C}{i}_L-\frac{1}{C}i$ Równania powyższe można zapisać w postaci zależności macierzowej równania stanu, w której zmiennymi stanu są prąd cewki i napięcie kondensatora $\left[\begin{array}{c}\frac{d{i}_L}{dt}\\ \frac{d{u}_C}{dt}\end{array}\right]=\left[\begin{array}{cc}\frac{-R}{L}& \frac{-1}{L}\\ \frac{1}{C}& 0\end{array}\right]\left[\begin{array}{c}{i}_L\\ u_C\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L}& \frac{R}{L}\\ 0& \frac{-1}{C}\end{array}\right]\left[\begin{array}{c}e\\ i\end{array}\right]$ Wektor stanu x jest równy $x=\left[\begin{array}{c}{i}_l\\ u_C\end{array}\right]$ a wektor wymuszeń $u=\left[\begin{array}{c}e\\ i\end{array}\right]$ Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu A jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz B zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: $R=2\mathrm{\Omega },L=1H,C=1F$ otrzymuje się macierz stanu A o postaci $A=\left[\begin{array}{cc}-2& -1\\ 1& 0\end{array}\right]$

---

Rozwiązanie równań różniczkowych metodą klasyczną W przypadku, gdy interesuje nas tylko jedna wybrana zmienna (jeden prąd bądź jedno napięcie w obwodzie) układ równań stanu pierwszego rzędu można sprowadzić do jednego równania różniczkowego n-tego rzędu względem tej zmiennej $a_n\frac{d^{n}x}{d{t}^n}+a_{n-1}\frac{d^{n-1}x}{d{t}^{n-1}}+a_{n-2}\frac{d^{n-2}x}{d{t}^{n-2}}+...+a_1\frac{dx}{dt}+a_{0}x=f(t)$ Rozwiązanie powyższego równania różniczkowego, podobnie jak w metodzie zmiennych stanu, można przedstawić w postaci sumy dwu składowych: ustalonej $x_u(t)$ wymuszonej przez źródło oraz składowej przejściowej $x_p(t)$ , zwanej również składową swobodną, pochodzącą od niezerowych warunków początkowych dla tej składowej. Składowa wymuszona stanowi rozwiązanie ustalone obwodu po komutacji i może być wyznaczona metodą symboliczną. Składowa przejściowa charakteryzuje fizycznie procesy zachodzące w obwodzie elektrycznym na skutek niezerowych warunków początkowych przy braku wymuszeń zewnętrznych. Odpowiada ona obwodowi, w którym wyeliminowano wszystkie zewnętrzne źródła wymuszające (źródła napięciowe zwarte a prądowe rozwarte).

---

Składowa przejściowa zależy jedynie od warunków początkowych odniesionych do tej składowej (napięć początkowych kondensatorów i prądów początkowych cewek), struktury obwodu i wartości parametrów tego obwodu. Dla obwodów elektrycznych zawierających elementy rozpraszające energię (rezystancje) składowa przejściowa, jak zostanie pokazane później, zanika z biegiem czasu do zera. Równanie składowej przejściowej otrzymuje się zakładając wymuszenie $f(t)$ we wzorze równe zeru i zastępując zmienną $x(t)$ poprzez jej składową przejściową $x_p(t)$ . Otrzymuje się wówczas równanie różniczkowe jednorodne o postaci $a_n\frac{d^n{x}_p}{d{t}^n}+a_{n-1}\frac{d^{n-1}{x}_p}{d{t}^{n-1}}+a_{n-2}\frac{d^{n-2}{x}_p}{d{t}^{n-2}}+...+a_1\frac{d{x}_p}{dt}+a_0{x}_p=0$ Rozwiązanie powyższego równania jednorodnego uzyskuje się za pośrednictwem równania charakterystycznego $a_n{s}^n+a_{n-1}{s}^{n-1}+a_{n-2}{s}^{n-2}+...+a_{1}s+a+a_0=0$ Jest to wielomian n-tego rzędu zmiennej zespolonej s o współczynnikach rzeczywistych $a_i$ Pierwiastki $s_i(i=1,2,...,n)$ tego wielomianu stanowią bieguny układu.

---

W tym punkcie ograniczymy się jedynie do przypadku biegunów pojedynczych. Przy takim założeniu rozwiązanie równania dla składowej przejściowej zapiszemy w postaci $x_p(t)={\mathrm{\Sigma }}_{i=1}^{n}A+i{e}^{5^{i}t}$ W rozwiązaniu tym współczynniki $A_i$ są stałymi całkowania, które należy wyznaczyć wykorzystując znajomość warunków początkowych w obwodzie (napięć kondensatorów i prądów cewek w chwili komutacji $t=0$). Z ciągłości prądów cewek i napięć kondensatorów wynika następująca zależność $x(0^{-})=x(0^{+})+x(0^{+})$ Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki $A_i$ i podstawia do wzoru ogólnego . Po wyznaczeniu rozwiązania obwodu dla składowej ustalonej i przejściowej rozwiązanie całkowite jest sumą obu rozwiązań cząstkowych, to znaczy $x(t)=x_u(t)+x_p(t)$ Powyższa procedura rozwiązania stanu nieustalonego w obwodzie poprzez rozwiązanie układu równań różniczkowych wyższego rzędu nosi nazwę metody klasycznej. Przy większej liczbie zmiennych jest ona dość uciążliwa w obliczeniach, gdyż wymaga pracochłonnego wyznaczania rozwiązań dla każdej składowej przejściowej zmiennych stanu. Dlatego w praktyce stosuje się zwykle tylko do równań pierwszego rzędu. W tej pracy pokażemy jej zastosowanie w rozwiązaniu stanu nieustalonego w obwodzie RL oraz RC przy załączeniu napięcia stałego.

---

Stan nieustalony w szeregowym obwodzie RL przy załączeniu napięcia stałego Rozpatrzmy stan nieustalony w obwodzie szeregowym RL przy zerowych warunkach początkowych i załączeniu napięcia stałego jak to zostało w symboliczny sposób przedstawione na rysunku Zerowe warunki początkowe obwodu oznaczają, że $i_L(0^{-})=0$ Po przełączeniu w obwodzie RL powstaje stan nieustalony, który po określonym czasie prowadzi do powstania nowego stanu ustalonego wynikającego z nowego układu połączeń elementów. Stan nieustalony jest superpozycją stanu ustalonego i przejściowego. Stan ustalony w obwodzie RL przy wymuszeniu stałym oznacza, że cewka stanowi zwarcie Na podstawie napięciowego prawa Kirchhoffa prąd ustalony tej cewki jest równy $i_{Lu}(t)\frac{E}{R}$

---

Przechodząc do obliczenia stanu przejściowego należy wyeliminować zewnętrzne źródło zasilające. Ponieważ jest to źródło napięciowe, należy go zewrzeć. Schemat obwodu dla stanu przejściowego po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona, ma postać przedstawioną na rysunku. Stosując prawo napięciowe Kirchhoffa dla tego obwodu przy uwzględnieniu $u_L{}_p=\frac{d{i}_{Lp}}{dt}$ otrzymuje się równanie różniczkowe jednorodne (brak wymuszenia) dla składowej przejściowej o postaci $L\frac{d{i}_{Lp}}{dt}+R{i}_{Lp}=0$ Równanie charakterystyczne odpowiadające powyższemu równaniu różniczkowemu przyjmuje postać $Ls+R=0$ Równanie to posiada tylko jeden pierwiastek $s_1=-\frac{R}{L}$ Wykorzystując wzór rozwiązanie stanu przejściowego dla prądu w obwodzie RL zapiszemy w postaci $i_{Lp}=A_1{e}^{-\frac{t}{L/R}}$ w której współczynnik $A_1$ jest nieznaną stałą całkowania. Rozwiązanie całkowite obwodu jest sumą składowej ustalonej i przejściowej. W związku z powyższym prąd cewki określony jest następującym wzorem $i_L(t)=i_{Lu}(t)+i_{Lp}(t)=\frac{E}{R}+A_1{e}^{-\frac{t}{L/R}}$

---

Z prawa komutacji dla cewki wynika, że $i_L(0^{-})=i_L(0+)$ , stąd wobec $i_L(0^{-})=0$ otrzymuje się $0=\frac{E}{R}+a_1$ oraz $A_1=-E/R$ Stąd rozwiązanie określające przebieg prądu cewki w stanie nieustalonym przyjmuje postać $i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{L/R}})$ Wprowadzając pojęcie stałej czasowej $\tau$ obwodu RL $\tau =\frac{L}{R}$ rozwiązanie na prąd cewki w stanie nieustalonym można zapisać w postaci $i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{\tau }})$ Jednostką stałej czasowej jest sekunda (jednostką indukcyjności jest $1H=1\mathrm{\Omega }s$ a jednostką rezystancji $1\mathrm{\Omega }$). Łatwo wykazać, że po upływie trzech stałych czasowych $(t=3\tau )$ prąd cewki uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po 5 stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony. Na rysunku poniżej przedstawiono przebiegi prądu cewki dla różnych wartości stałej czasowej Jest to przebieg typu wykładniczego, w którym stan przejściowy trwa tym dłużej im dłuższa jest stała czasowa. Praktycznie po 5 stałych czasowych stan przejściowy w obwodzie zanika przechodząc w stan ustalony.

---

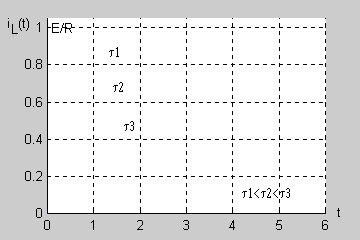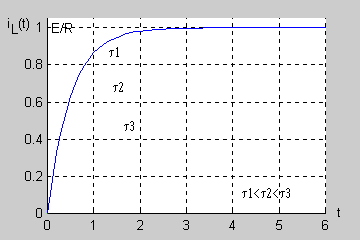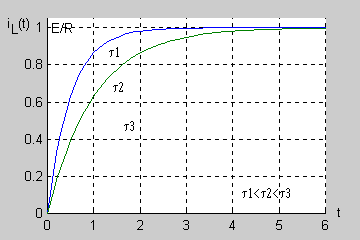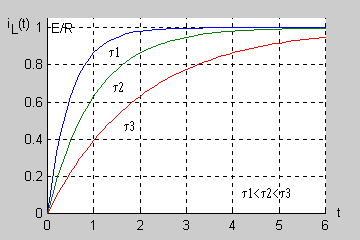
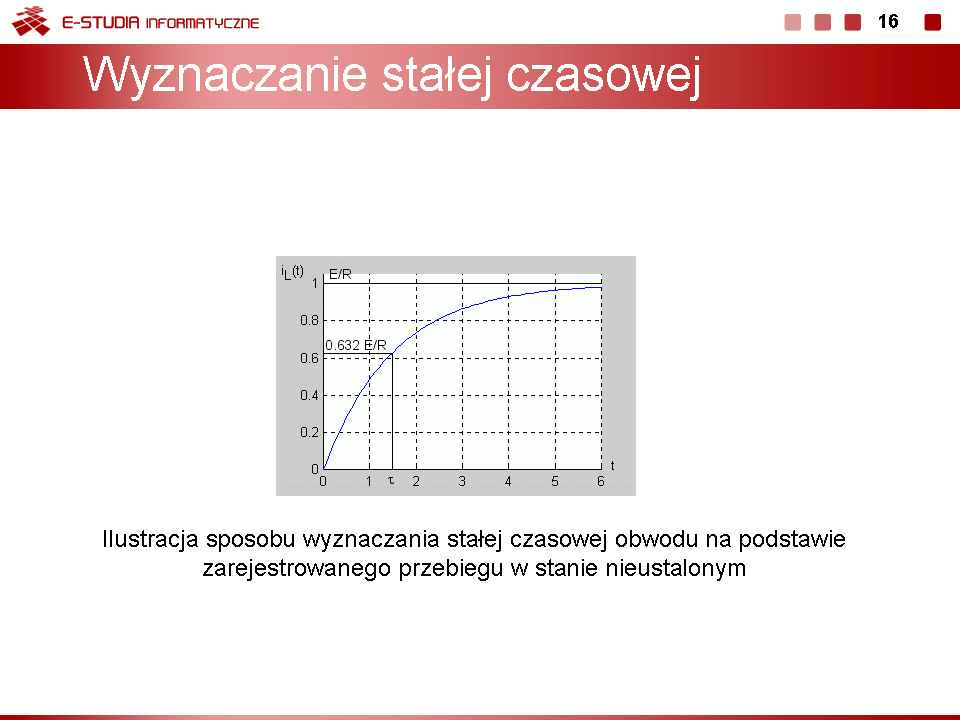
Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość $i_L(\tau )=\frac{E}{R}(1-e^{-1})=0,632\frac{E}{R}$ Oznacza to, że wartość prądu $i_L(t){|}_{t=\tau }=0,632\frac{E}{R}$ wyznacza na osi odciętych wartość stałej czasowej. Sposób wyznaczania stałej czasowej zilustrowany jest na rysunku

---

Wyznaczenie rozwiązania na prąd w stanie nieustalonym w obwodzie RL pozwala na określenie przebiegu czasowego pozostałych wielkości w obwodzie. Korzystając z zależności definicyjnej cewki $u_L=L\frac{d{i}_L}{dt}$ otrzymuje się $u_L(t)=L\frac{d{i}_L(t)}{dt}=E{e}^{-\frac{t}{L/R}}$ Przebieg napięcia na cewce w stanie nieustalonym w obwodzie szeregowym RL przedstawiono na rysunku Napięcie na rezystorze R, jak wynika z prawa Ohma, jest proporcjonalne do prądu $u_R(t)=R{i}_L(t)=E(1-e^{-\frac{t}{L/R}})$

---

Stan nieustalony w gałęzi szeregowej RC przy załączeniu napięcia stałego Rozpatrzymy stan nieustalony w obwodzie szeregowym RC przy zerowych warunkach początkowych i załączeniu napięcia stałego Wobec braku zasilania w obwodzie przed przełączeniem w warunki początkowe obwodu są zerowe, co oznacza, że . Po przełączeniu powstaje w obwodzie stan nieustalony, który po pewnym czasie prowadzi do powstania nowego stanu ustalonego. Stan nieustalony obwodu jest superpozycją stanu ustalonego i przejściowego. Stan ustalony w obwodzie RC przy wymuszeniu stałym $(\omega =0)$ oznacza, że kondensator stanowi przerwę Zgodnie z prawem napięciowym Kirchhoffa napięcie ustalone kondensatora jest równe $u_{Cu}(t)=E$

---

Schemat obwodu dla stanu przejściowego (po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona) ma postać przedstawioną na rysunku Stosując prawo napięciowe Kirchhoffa dla tego obwodu i uwzględniając, że $i_{Cp}=C\frac{d{u}_{Cp}}{dt}$ , otrzymuje się równanie różniczkowe jednorodne o postaci $RC\frac{d{u}_{Cp}}{dt}+u_{Cp}=0$ Równanie charakterystyczne odpowiadające mu przyjmuje więc postać $RCs+1=0$ Równanie to posiada jeden pierwiastek $s_1=-1/(RC)$ W związku z powyższym jego rozwiązanie wynikające ze wzoru przyjmie uproszczoną postać $u_{Cp}=A_1{e}^{s_{1}t}=A_1{e}^{-\frac{t}{RC}}$ W rozwiązaniu tym współczynnik $A_1$ jest stałą całkowania, którą należy wyznaczyć korzystając z prawa komutacji. Rozwiązanie całkowite będące sumą składowej ustalonej i przejściowej przybiera więc postać $u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1{e}^{-\frac{t}{RC}}$

Z prawa komutacji dla kondensatora wynika, że $u_C(0^{-})=u_C(0^{+})$ , stąd wobec $u_C(0^{-})=0$ otrzymuje się $0=E+A_1$ oraz $A_1=-E$ Rozwiązanie czasowe określające przebieg napięcia na kondensatorze przyjmuje więc postać $u_C(t)=E(1-e6-\frac{t}{RC})$ Wprowadzając pojęcie stałej czasowej obwodu RC jako iloczynu rezystancji R i pojemności C $\tau =RC$ rozwiązanie na napięcie kondensatora w stanie nieustalonym można zapisać w postaci $u_C(t)=E(1-e^{-\frac{t}{\tau }})$ Jak łatwo sprawdzić podstawową jednostką stałej czasowej w obwodzie RC jest również sekunda (jednostką rezystancji jest $1\mathrm{\Omega }=1V/A$, a jednostką pojemności jest $1F=1As/V$). Na rysunku przedstawiono przebiegi napięcia na kondensatorze w stanie nieustalonym $u_C(t)=E(1-e^{-\frac{t}{\tau }})$ dla różnych wartości stałej czasowej. Im dłuższa stała czasowa tym dłużej trwa stan przejściowy w obwodzie (zanikanie zmian napięcia do zera).

---

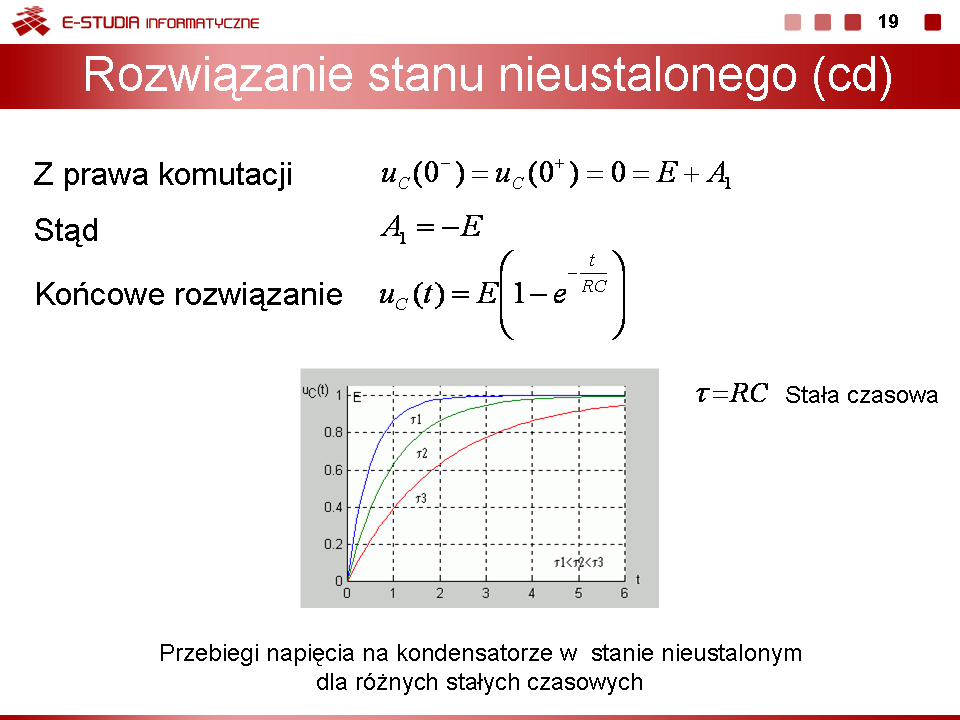
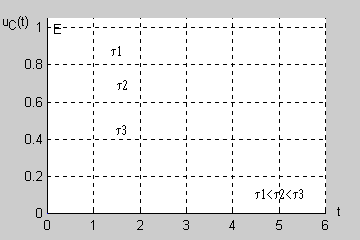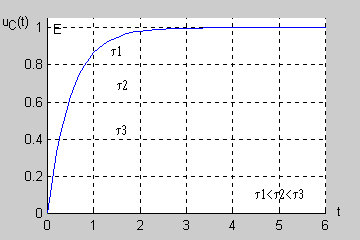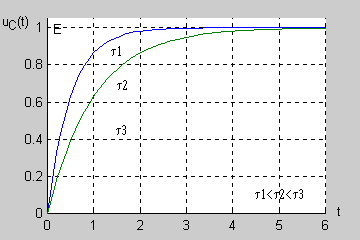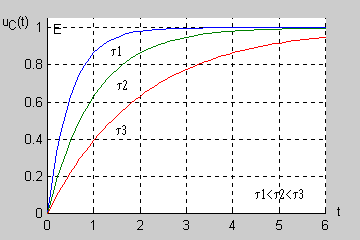
Łatwo wykazać, że po upływie 3 stałych czasowych ( ) napięcie uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony. Stałą czasową można wyznaczyć bezpośrednio na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i pojemności, podobnie jak to miało miejsce w przypadku obwodu RL.

---

Po określeniu funkcji opisującej przebieg napięcia na kondensatorze można określić przebieg czasowy prądu w obwodzie. Korzysta się przy tym z zależności definicyjnej kondensatora $i_C=C\frac{d{u}_C}{dt}$, zgodnie z którą $i_C(t)=C\frac{d{u}_c(t)}{dt}=\frac{E}{R}{e}^{-\frac{t}{RC}}$ Przebieg prądu ładowania kondensatora w stanie nieustalonym w obwodzie RC dla różnych stałych czasowych przedstawia rysunek W chwili komutacji występuje skokowa zmiana wartości prądu (prąd kondensatora nie jest objęty komutacyjnym prawem ciągłości). Przebieg prądu kondensatora dąży do wartości ustalonej zerowej (w stanie ustalonym kondensator stanowi przerwę dla prądu). Stała czasowa zmian tego prądu jest identyczna jak napięcia i równa $\tau =RC$.

---

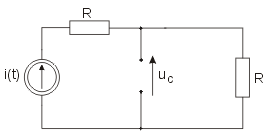
Zadania sprawdzające Zadanie 7.1 Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: $L=1H,C=0,5F,R=1\mathrm{\Omega },e(t)=10\sqrt{2}sin(t_4{5}^o)V,i(t)=2sin(t-45^o)A$ Rozwiązanie Warunki początkowe dotyczą stanu ustalonego przed przełączeniem, w którym w obwodzie działają oba źródła wymuszające. Stosując metodę symboliczną analizy obwodu otrzymujemy $E=10e^{j45^o}$ $I=\frac{2}{\sqrt{2}}{e}^{-j45o}$ $\omega =1$ $Z_L=j\omega L=j1$ $Z_C=-j/\omega C=-j2$

---

Równania obwodu w stanie ustalonym $E=Z_L{I}_L+R(I+I_L)$ $I_L=\frac{E-RI}{R+Z_L}=7,21e^{j11,31^o}$ $U_C=Z_{C}I=\frac{4}{\sqrt{2}}{e}^{-j135^0}$ $i_L(t)=7,21\sqrt{2}sin(t+11,31^o)$ $u_C(t)=4sin(t-135^o)$ Warunki początkowe: $i_L(0^{-})=2$ $u_C(0^{-})=-2\sqrt{2}$

---

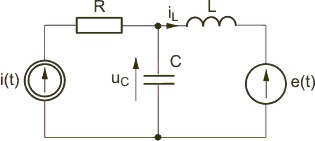
Zadanie 7.2 Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku Rozwiązanie Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika $i(t)=i_L+C\frac{d{u}_C}{dt}$ $e(t)=u_C-L\frac{d{i}_L}{dt}$ Po przekształceniach tych równań otrzymujemy $\frac{d{u}_C}{dt}=\frac{1}{C}[i(t)-i_L]$ $\frac{d{u}_L}{dt}=\frac{1}{L}[u_C-e(t)]$ Równanie stanu: $\left[\begin{array}{c}\frac{d{u}_C}{dt}\\ \frac{d{i}_L}{dt}\end{array}\right]=\left[\begin{array}{cc}0& -1/C\\ 1/L& 0\end{array}\right]\cdot \left[\begin{array}{c}{u}_C\\ i_L\end{array}\right]+\left[\begin{array}{cc}0& 1/C\\ -1/L& 0\end{array}\right]\cdot \left[\begin{array}{c}e(t)\\ i(t)\end{array}\right]$ Zadanie 7.3 Określić przebieg czasowy napięcia na kondensatorze w stanie nieustalonym w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów: $R=10k\mathrm{\Omega },C=10\mu F,i(t)=I=2mA$. 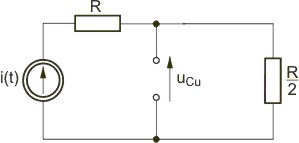Rozwiązanie Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego $u_C(t)=u_C(0^{-})=IR=20V$ Stan ustalony w obwodzie po przełączeniu dotyczy obwodu przedstawionego na rysunku Schemat obwodu w stanie ustalonym po przełączeniu $u_C{}_u(t)=u_C{}_u(0^{+})=IR/2=10V$ Stan przejściowy dotyczy obwodu po przełączeniu przedstawionego na rysunku Schemat obwodu w stanie przejściowym po przełączeniu Równania różniczkowe obwodu: $u_C{}_p+C\frac{R}{2}\frac{d{u}_{Cp}}{dt}=0$ $u_C{}_p+0,05\frac{d{u}_{Cp}}{dt}=0$ Równanie charakterystyczne: $1+0,05s=0\to s_1=-20$ Rozwiązanie równania różniczkowego jednorodnego $u_C{}_p(t)$ oraz rozwiązanie całkowite u_C(t) $U_C{}_p(t)=A{e}^{-20t}$ $U_C(t)=u_C{}_p(t)+u_C{}_p(t)=10_A{e}^{-20t}$ Z prawa komutacji dla kondensatora wynika równość $u_C(0^{-})=u_C(0^{+})\to 20=10+A\to A=10$ Postać ostateczna rozwiązania: $u_C(t)=10(1+e^{-20t})$ Stała czasowa obwodu jest więc równa $\tau =1/20=0,05s$