PF Moduł 8

Wprowadzenie Omówione są tu ogólne prawa makroskopowe opisujące prawidłowo zjawiska cieplne i pozwalające ilościowo przewidywać skutki różnych procesów.

---

Oznaczamy przez $\mathrm{\Delta }U$ zmianę energii wewnętrznej układu, który przechodzi ze stanu o energii wewnętrznej $U_1$ do stanu o energii wewnętrznej $U_2$. Zmiana ta może zachodzić na kilka sposobów: przez wykonanie pracy W nad układem lub przez układ nad otoczeniem, przez wymianę ciepła Q między układem i otoczeniem, przez wymianę materii M pomiędzy układem, a otoczeniem. Zapiszemy to następująco $\mathrm{\Delta }U=U_2-U_1=W+Q+M$ Wzór ten wyraża zasadę zachowania energii w procesach termodynamicznych i nosi nazwę pierwszej zasady termodynamiki. Zasada ta może, być sformułowana w następujący sposób: Przyrost energii wewnętrznej układu przy przejściu ze stanu początkowego do końcowego równy jest sumie dostarczonej do układu energii cieplnej, wykonanej nad układem pracy oraz energii uzyskanej wskutek wymiany materii z otoczeniem. Przyrost ten nie zależy od sposobu, w jaki dokonuje się przejście, a określony jest całkowicie przez początkowy i końcowy stan układu. Niemożliwe jest skonstruowanie silnika cyklicznego, który pracowałby bez pobierania z otoczenia energii. Taki hipotetyczny silnik nazwano perpetuum mobile I-go rodzaju. Niekiedy formułuje się pierwszą zasadę termodynamiki jako niemożliwość skonstruowania perpetuum mobile pierwszego rodzaju to jest skonstruowanie silnika cyklicznego, który pracowałby bez pobierania z otoczenia energii. Zaczerpnięty z łaciny zwrot "perpetuum mobile" znaczy "wiecznie poruszający się".

---

W ten sposób pierwsza zasada termodynamiki wskazuje na trzy różne sposoby zmiany energii wewnętrznej układu: na drodze wykonywania pracy nad układem bądź przez układ oraz poprzez wymianę ciepła lub/i materii pomiędzy układem a otoczeniem.

---

W naszych dalszych rozważaniach będziemy omawiać układy nie wymieniające materii z otoczeniem, dla których M=0. Zmiana energii wewnętrznej $\mathrm{\Delta }U$ układu o stałej masie dokonuje się poprzez wymianę ciepła $Q$, co zachodzi w warunkach różnicy temperatur pomiędzy układem i otoczeniem, lub/i poprzez pracę $W$ wykonaną nad układem lub przez układ nad otoczeniem. $\mathrm{\Delta }Q=Q+W$. Wprowadzamy tu konwencję, którą będziemy stosować w dalszych rozważaniach dla układów nie wymieniających materii z otoczeniem. Praca $W$ jest dodatnia $(W>0)$, jeżeli jest wykonywana przez siły zewnętrzne (otoczenie) nad układem fizycznym. Kiedy układ fizyczny wykonuje pracę nad otoczeniem (kosztem swej energii wewnętrznej) praca ta jest ujemna $(W<0)$. Podobnie, ciepło jest dodatnie $(Q>0)$, jeśli przepływa z otoczenia do układu, a ujemne $(Q<0)$, jeśli przepływa z układu do otoczenia. Dla przykładu, kiedy siły zewnętrzne (otoczenie) wykonują pracę sprężając gaz $(\mathrm{\Delta }V<0)$, to wykonana praca jest dodatnia, kiedy gaz wykonuje pracę nad otoczeniem rozprężając się $(\mathrm{\Delta }V>0)$, praca jest ujemna.

---

Dla wyznaczenia skończonej pracy wykonanej w procesie kwazistatycznym, odwracalnym, można rozpatrywać przemianę jako ciąg procesów elementarnych, w których zmiany parametrów układu są nieskończenie małe. Dla procesu elementarnego zapiszemy pierwsza zasadę termodynamiki w postaci $dU=\delta Q+\delta W$ UWAGA: Symbolami $\delta Q$ i $\delta W$ oznaczamy różniczkowe porcje (a nie skończone przyrosty) wymienianego przez układ ciepła i wykonanej pracy przy nieskończenie małych (infinitezymalnych) zmianach parametrów stanu układu. Wynika, to z faktu, ze ciepło i praca nie są funkcjami stanu, bowiem jak zobaczymy, zależą od drogi przejścia pomiędzy stanami. Mówimy, że są funkcjami procesu. Symbol $dU$ oznacza zmianę energii wewnętrznej, która jest funkcją stanu. W przemianie kołowej, kiedy układ powraca do stanu początkowego, jego energia wewnętrzna mieć będzie taką samą wartość jak w stanie początkowym, co zapisujemy w postaci $\oint dU=0$ Nieskończenie mały przyrost, dla którego spełniony jest powyższy warunek nazywamy różniczką zupełną. Kiedy warunek ten nie jest spełniony, mamy do czynienia z wyrażeniem różniczkowym. Różniczkami zupełnymi są nieskończenie małe przyrosty funkcji stanu, ale nie są nimi infinitezymalne ilości wymienianego ciepła, lub wykonanej pracy. Bilans ilości ciepła pobranego i oddanego przez układ w przemianie kołowej lub wykonanej przez układ pracy nie musi być równy zeru.

---

Przemiana izochoryczna to proces, w którym objętość układu pozostaje stała, czyli $V=const$. W przemianie tej nie jest wykonywana praca. W oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację $\delta Q_v=du$, co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła. Pojemność cieplna jednego mola, tzw. ciepło molowe substancji w procesie przebiegającym bez zmiany objętości wyraża się wzorem $C_v=(\frac{\partial U}{\partial T}{)}_v$, gdzie indeks v przy znaku pochodnej cząstkowej oznacza, że proces zachodzi w stałej objętości. Energia wewnętrzna danej masy gazu doskonałego zależy jednak wyłącznie od temperatury. Przekonuje nas o tym doświadczenie J.P. Joule'a z rozprężaniem rozrzedzonego gazu do próżni, gdy układ jest w osłonie izolacyjnej uniemożliwiającej wymianę ciepła z otoczeniem. Możemy wiec dla gazu doskonałego napisać, że $C_v=\frac{dU}{dT}$. W dowolnym procesie kwazistatycznym, odwracalnym, niezależnie, która z wielkości jest stała zmiana energii wewnętrznej $n_M$ moli gazu doskonałego jest określona wzorem: $dU=n_M\cdot C_v\cdot dT$. Bardziej szczegółowe uzasadnienie tego wzoru, w oparciu o analizę doświadczenia Joule'a, można znaleźć w literaturze. Zapamiętajmy, że powyższy wzór, określający zmianę energii wewnętrznej, ma charakter uniwersalny. Mimo że został sformułowany dla przypadku przemiany izochorycznej i występuje w nim ciepło molowe $C_v$, może być stosowany przy opisie innych przemian gazowych, gdyż energia wewnętrzna jest funkcją stanu. Informacja ta jest bardzo użyteczna przy rozwiązywaniu zadań.

---

Jeśli proces zachodzi pod stałym ciśnieniem, czyli $p=const$, to mówimy, że zachodzi przemiana izobaryczna. Z równania stanu wynika, że w tym przypadku objętość jest liniową funkcją temperatury. Przy wzroście objętości praca jest wykonywana przez gaz $(W<0,W^{\prime }>0)$, a przy zmniejszeniu objętości, przez otoczenie, $(W>0,W^{\prime }<0)$ Ciśnienie zachowuje stałą wartość, więc praca wykonana nad układem w przemianie izobarycznej wynosi $W=-\underset{V_1}{\overset{V_2}{\int }}p\cdot dV=-p\cdot \underset{V_1}{\overset{V_2}{\int }}dV=p\cdot (V_1-V_2)$. Podwyższenie temperatury o jeden kelwin wymaga więcej ciepła niż w przypadku ogrzewania bez zmiany objętości, bowiem część ciepła zużywana jest na wykonanie pracy. W procesie izobarycznym energię wewnętrzną możemy zmienić zarówno na drodze wykonania pracy jak i wymiany ciepła $dU=\delta Q_p-p\cdot dV$. Wyrażenie to możemy przepisać dla $n_M$ moli w innej postaci wykorzystując poznane wzory: $n_M\cdot C_v\cdot dT=n_M\cdot C_p\cdot dT-p\cdot dV$ gdzie wprowadziliśmy pojęcie ciepła molowego przy stałym ciśnieniu $C_p=\frac{\delta Q_p}{dT}$. Różniczkując równanie stanu dla procesu izobarycznego, w którym $p=const$ mamy $p\cdot dV=n_M\cdot R\cdot dT$ Wykorzystując ten związek możemy napisać, że $n_M\cdot C_v\cdot dT=n_M\cdot C_p\cdot dT-n_M\cdot R\cdot dT$ skąd otrzymujemy równanie Mayera $C_p=C_v+R$. Stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości jest parametrem określającym rodzaj gazu i oznaczany jest zwykle symbolem $\kappa$ (kappa). $\kappa =\frac{C_p}{C_v}$. Wykorzystując równanie Mayera można ciepła molowe $C_p$ i $C_v$ wyrazić za pomocą współczynnika $\kappa$. $\kappa =\frac{C_v+R}{C_v}=1+\frac{R}{C_v}$ lub $C_v=\frac{R}{\kappa -1}$, $C_p=\frac{\kappa \cdot R}{\kappa -1}$. Ze związków tych widzimy, że $\kappa >1$.

---

Jeśli dany proces zachodzi w stałej temperaturze, czyli $T=const$, to mówimy, że zachodzi przemiana izotermiczna. Z równania stanu gazu wynika natychmiast, że w przemianie tej ciśnienie gazu jest odwrotnie proporcjonalne do jego objętości, bowiem dla danej masy gazu wyrażonej w molach mamy $p\cdot V=n_M\cdot R\cdot T$, czyli $p=\frac{const}{V}$. Związek ten zwany jest prawem Boyle'a Mariotte'a. Pracę wykonaną nad układem przy przemianie izotermicznej wyznaczamy z jej definicji oraz korzystając z równania stanu dla przemiany izotermicznej. $W=-\underset{V_1}{\overset{V_2}{\int }}p\cdot dV=-n_M\cdot R\cdot T\cdot \underset{V_1}{\overset{V_2}{\int }}\frac{dV}{V}=$ $-n_M\cdot R\cdot T(ln{V}_2-ln{V}_1)=n_M\cdot R\cdot T\cdot ln(\frac{V_1}{V_2})$ Zapiszmy pierwsza zasadę termodynamiki dla przemiany izotermicznej w postaci różniczkowej, $dU=\delta Q_T-p\cdot dV$. W przemianie izotermicznej $T=const$, więc $dU=0$. Oznacza to, że w przemianie izotermicznej energia wewnętrzna układu nie zmienia się. Widzimy dalej, że temperatura układu jest stała, ale jest wymieniane ciepło między układem i otoczeniem. Ilość tego ciepła możemy określić $0=\delta Q_T-p\cdot dV$, czyli $\delta Q_T=p\cdot dV$. Wymiana ciepła następuje, na skutek wykonanej pracy. Jeśli praca jest wykonywana nad układem $(\delta W>0)$, to ciepło w równej ilości musi być oddawane do otoczenia $(\delta Q<0)$ i vice versa.

---

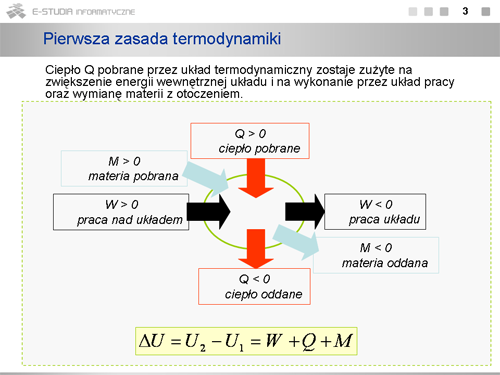
Przemiana, która zachodzi bez wymiany ciepła z otoczeniem - to przemiana adiabatyczna. Dla przemiany tej mamy $\delta Q=0$. W takim przypadku pierwsza zasada termodynamiki przyjmie postać $dU=-p\cdot dV$, co oznacza, że w przemianie tej energię wewnętrzną można zmienić jedynie poprzez wykonanie pracy. Zapiszmy to bardziej szczegółowo $dU=-p\cdot dV$, czyli $n_M\cdot C_v\cdot dT+\frac{n_M\cdot R\cdot T}{V}\cdot dV=0$. Można to zapisać nieco inaczej dzieląc obustronnie ostatnie równanie przez $n_M\cdot C_v\cdot T$ $\frac{dT}{T}+\frac{R}{C_v}\cdot \frac{dV}{V}=0$. Pamiętając z matematyki, że $d(lnx)=dx/x$ oraz, że różniczka sumy równa jest sumie różniczek, możemy to równanie przepisać w postaci $d(lnT+\frac{R}{C_v}\cdot lnV)=0$. Jeśli różniczka funkcji równa jest zeru, to funkcja równa jest stałej, czyli $lnT+\frac{R}{C_v}\cdot lnV=const$. Pamiętając, że $R/C_v=\kappa -1$ mamy $lnT+(\kappa -1)\cdot lnV=const$, lub $ln(T\cdot V^{\kappa -1})=const$. Jeśli logarytm funkcji równy jest stałej, to i sama funkcja pozostaje stała. Możemy wiec napisać $T\cdot V^{\kappa -1}=const$. 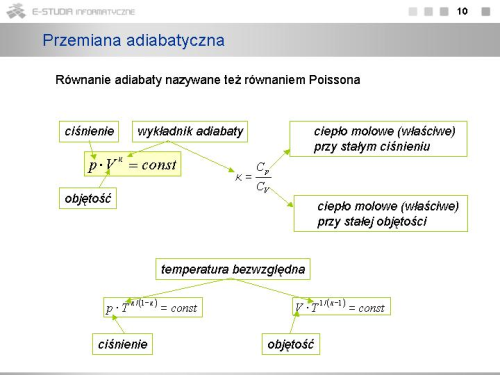Wykorzystując równanie stanu gazu doskonałego pV = RT dostajemy $\frac{p\cdot V}{R}\cdot V^{\kappa -1}=const$ lub $\frac{p\cdot V^{\kappa }}{R}=const$. Powyższe wzory pozostaną w mocy, jeśli stałą gazową $R$ włączymy do stałej po prawej stronie. Otrzymamy wtedy $p\cdot V^{\kappa }=const$. Związek ten jest równaniem adiabaty i nosi nazwę równania Poissona. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej $p\cdot T^{\kappa /(1-\kappa )}=const,V\cdot T^{1/(\kappa -1)}=const$. 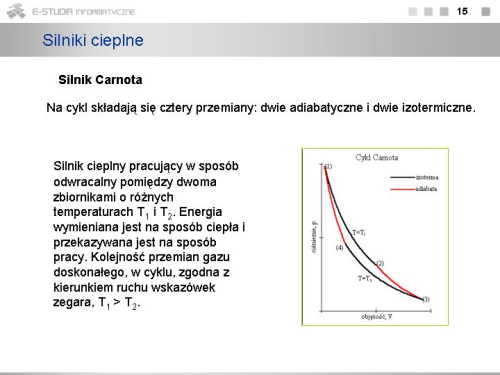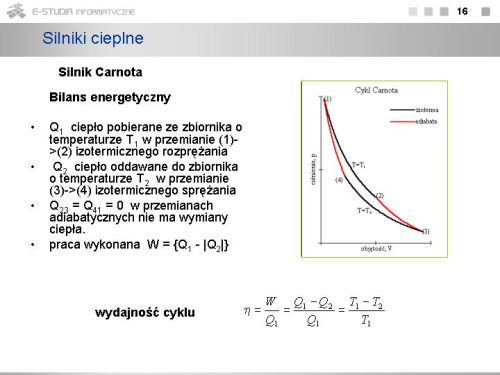Realizacja przemiany adiabatycznej jest trudna, gdyż wymaga idealnej izolacji cieplnej gazu od otoczenia. Warto jednak zauważyć, że gdy sprężanie lub rozprężanie gazu zachodzi bardzo szybko, to nawet mimo nie najlepszej izolacji cieplnej przemiana taka ma charakter bardzo zbliżony do przemiany adiabatycznej. Właściwość tę wykorzystuje się w pracy silników cieplnych.

---

---

---

---

---

---

---

---

---

---

---