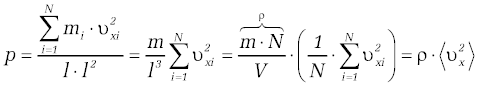PF Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 90: | Linia 90: | ||
<math>p\cdot V=\frac{1}{3}\cdot\rho\left\langle v^2\right\rangle\cdot V=\frac{1}{3}\cdot \begin{matrix} n_M\cdot M \\ \overbrace{ \rho\cdot V} \end{matrix}\cdot \left\langle v^2\right\rangle </math> | <math>p\cdot V=\frac{1}{3}\cdot\rho\left\langle v^2\right\rangle\cdot V=\frac{1}{3}\cdot \begin{matrix} n_M\cdot M \\ \overbrace{ \rho\cdot V} \end{matrix}\cdot \left\langle v^2\right\rangle </math> | ||
We wzorze tym iloczyn gęstości i objętości jest po prostu masą gazu, którą następnie wyraziliśmy w molach oznaczając przez <math>M\,</math> jego masę molową. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd9.png]] | |||
|valign="top"|Teraz masę gazu wyraziliśmy w molach, oznaczając przez <math>M\,</math> jego masę molową. Mnożąc stronami przez <math>3/2\,</math> i dzieląc przez liczbę Avogadro otrzymujemy | |||
:<math>\frac{1}{2}\cdot \begin{matrix} m_0 \\ \overbrace{ \frac{M}{N_A} } \end{matrix} \cdot \left\langle v^2\right\rangle=\frac{3}{2}\cdot \begin{matrix} k \\ \overbrace{ \frac{R}{N_A} } \end{matrix}\cdot T</math> | |||
Zauważamy przy tym, że masa molowa podzielona przez liczbę Avogadro to po prostu masa jednej cząsteczki <math>m_0\,</math> . Iloraz stałej gazowej i liczby Avogadro, to stała Boltzmanna <math>k\,</math> . Stała ta ma sens stałej gazowej odniesionej do jednej cząsteczki. Jak zobaczymy, stała ta odgrywa fundamentalna rolę w fizyce. | |||
Wykorzystując wprowadzone oznaczenia możemy przepisać ostatnie równanie w postaci | |||
<math>\frac{1}{2}\cdot m_0\cdot\left\langle v^2\right\rangle=\left\langle\frac{1}{2}\cdot m_0\cdot v^2\right\rangle=\frac{3}{2}\cdot k\cdot T</math> | |||