PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 170: | Linia 170: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd13.png]] | ||
|valign="top"|Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na | |valign="top"|Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. | ||
|} | |} | ||
| Linia 177: | Linia 177: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd14.png]] | ||
|valign="top"| | |valign="top"|Rozwiązanie obwodu przebiega w następującej kolejności. | ||
Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu: | |||
<math>I=\frac{5}{\sqrt2}e^{j45^o}</math> | <math>I=\frac{5}{\sqrt2}e^{j45^o}</math> | ||
| Linia 187: | Linia 188: | ||
<math>Z_M=j\omega M=j1</math> | <math>Z_M=j\omega M=j1</math> | ||
Impedancja zastępcza obwodu wobec <math>Z_2=0</math> | Impedancja zastępcza obwodu wobec <math>Z_2=0</math> | ||
<math>Z=\frac{RZ_M}{R+Z_M}=\frac{1}{\sqrt2}e^{j45^o}</math> | <math>Z=\frac{RZ_M}{R+Z_M}=\frac{1}{\sqrt2}e^{j45^o}</math> | ||
| Linia 199: | Linia 200: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd15.png]] | ||
|valign="top"|Napięcie <math> | |valign="top"|Napięcie <math>U_{AB}\,</math> | ||
<math>U_{AB}=ZI=j5</math> | <math>U_{AB}=ZI=j5</math> | ||
| Linia 206: | Linia 206: | ||
Prądy: | Prądy: | ||
<math>I_R=\frac{U_{AB}}{R}=j5</math> | <math>I_R=\frac{U_{AB}}{R}=j5</math> | ||
<math>I_1=0</math> | <math>I_1=0</math> | ||
<math>I_2=I_3\frac{U_{AB}}{Z_M}=5</math> | <math>I_2=I_3\frac{U_{AB}}{Z_M}=5</math> | ||
Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą <math>U_{AB}=j5</math> Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie | Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą <math>U_{AB}=j5</math>. Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie | ||
<math>U_{L_1}=j\omega L_1I_1+j\omega MI_2=j5</math> | <math>U_{L_1}=j\omega L_1I_1+j\omega MI_2=j5</math> | ||
<math>U_{L_2}=j\omega L_2I_2+j\omega MI_1=j5</math> | <math>U_{L_2}=j\omega L_2I_2+j\omega MI_1=j5</math> | ||
| Linia 231: | Linia 226: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd16.png]] | ||
|valign="top"| | |valign="top"|'''Podstawy fizyczne działania transformatora''' | ||
'''Podstawy fizyczne działania transformatora''' | |||
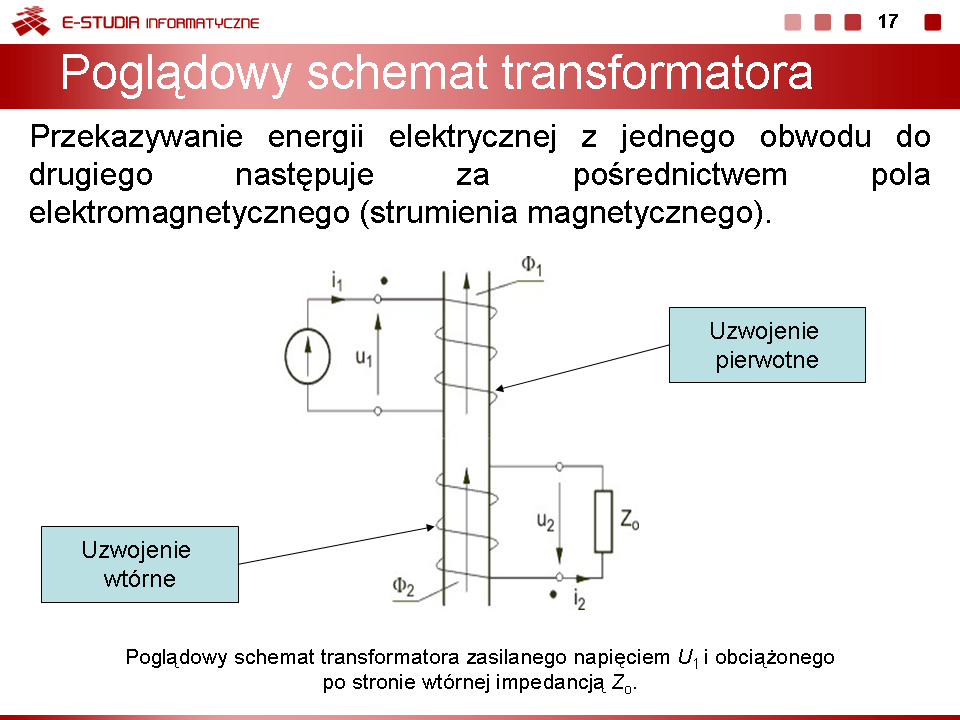
Transformator jest układem przetwarzającym napięcie wejściowe w napięcie wyjściowe za pośrednictwem strumienia magnetycznego przy braku bezpośredniego połączenia galwanicznego między obu zaciskami (wejściowymi i wyjściowymi). Transformatory mogą być stosowane do różnych celów, ale podstawowym ich zadaniem jest zmiana wartości napięcia wejściowego na inną wartość napięcia wyjściowego. Może to być zarówno podwyższenie jak i obniżenie wartości. Przy zmianie napięcia ulegają odpowiedniej zmianie również prądy w uzwojeniach transformatora. | Transformator jest układem przetwarzającym napięcie wejściowe w napięcie wyjściowe za pośrednictwem strumienia magnetycznego przy braku bezpośredniego połączenia galwanicznego między obu zaciskami (wejściowymi i wyjściowymi). Transformatory mogą być stosowane do różnych celów, ale podstawowym ich zadaniem jest zmiana wartości napięcia wejściowego na inną wartość napięcia wyjściowego. Może to być zarówno podwyższenie jak i obniżenie wartości. Przy zmianie napięcia ulegają odpowiedniej zmianie również prądy w uzwojeniach transformatora. | ||
Wersja z 12:50, 24 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
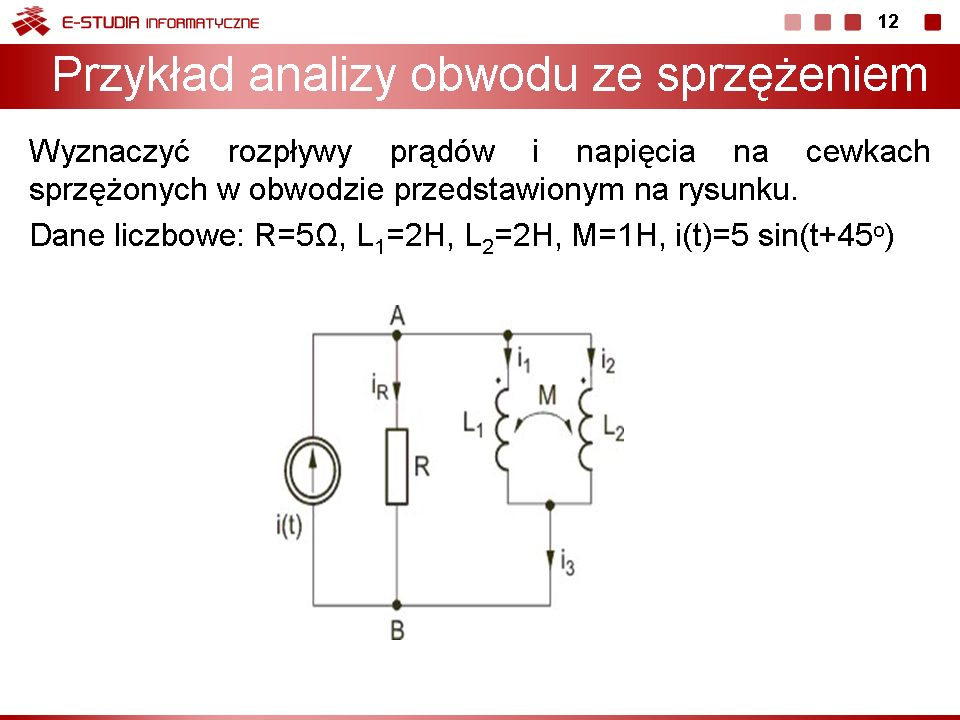
|
Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym.
Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. |

|
Rozwiązanie obwodu przebiega w następującej kolejności.
Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu:
|

|
PRZYKŁAD
Wyznaczyć rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej . Przyjąć następujące wartości parametrów obwodu: |

|
Rozwiązanie
Wielkości symboliczne charakteryzujące elementy obwodu:
|

|
Po wstawieniu wartości liczbowych otrzymuje się
Po uproszczeniu tego układu równań otrzymuje się
Stąd
Łatwo sprawdzić, że stosunek prądu do prądu podczas gdy
|