PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 140: | Linia 140: | ||
W obu przypadkach otrzymuje się obwody bez sprzężeń, równoważne oryginalnym jedynie pod względem prądowym. Napięcia w obu obwodach w części podlegającej przekształceniu są całkowicie różne. Rzeczywiste napięcia panujące na elementach podlegających transformacji powinny być określane bezpośrednio na podstawie obwodu oryginalnego i powinny uwzględniać sprzężenie magnetyczne | W obu przypadkach otrzymuje się obwody bez sprzężeń, równoważne oryginalnym jedynie pod względem prądowym. Napięcia w obu obwodach w części podlegającej przekształceniu są całkowicie różne. Rzeczywiste napięcia panujące na elementach podlegających transformacji powinny być określane bezpośrednio na podstawie obwodu oryginalnego i powinny uwzględniać sprzężenie magnetyczne | ||
Należy podkreślić, że przy wielu cewkach sprzężonych ze sobą, eliminacja każdego sprzężenia między dwoma wybranymi cewkami może zachodzić niezależnie od pozostałych sprzężeń, co znakomicie ułatwia przeprowadzenie procesu eliminacji sprzężeń. | Należy podkreślić, że przy wielu cewkach sprzężonych ze sobą, eliminacja każdego sprzężenia między dwoma wybranymi cewkami może zachodzić niezależnie od pozostałych sprzężeń, co znakomicie ułatwia przeprowadzenie procesu eliminacji sprzężeń. | ||
| Linia 149: | Linia 148: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd11.png]] | ||
|valign="top"| | |valign="top"|Jako przykład rozpatrzymy eliminację sprzężeń 3 cewek sprzężonych magnetycznie ze sobą. | ||
Na rysunku obok przedstawiony jest obwód zawierający trzy cewki sprzężone magnetycznie ze sobą. Stosując metodę eliminacji sprzężeń do każdej pary cewek sprzężonych ze sobą otrzymuje się schemat obwodu bez sprzężeń, równoważny pod względem prądowym obwodowi ze sprzężeniami | |||
Na rysunku przedstawiony jest obwód zawierający trzy cewki sprzężone magnetycznie ze sobą. Stosując metodę eliminacji sprzężeń do każdej pary cewek sprzężonych ze sobą otrzymuje się schemat obwodu bez sprzężeń, równoważny pod względem prądowym obwodowi ze sprzężeniami | |||
Przy analizie obwodów elektrycznych zawierających sprzężenia magnetyczne pierwszym krokiem jest eliminacja sprzężeń magnetycznych zgodnie z zasadami podanymi wyżej. Dzięki temu każdy element obwodu staje się uzależniony jedynie od swojego prądu. | Przy analizie obwodów elektrycznych zawierających sprzężenia magnetyczne pierwszym krokiem jest eliminacja sprzężeń magnetycznych zgodnie z zasadami podanymi wyżej. Dzięki temu każdy element obwodu staje się uzależniony jedynie od swojego prądu. | ||
'''Schemat obwodu po eliminacji sprzężeń jest równoważny obwodowi oryginalnemu jedynie pod względem prądowym.''' Stąd obwód taki może służyć wyłącznie obliczeniu prądów. Dla wyznaczenia napięć gałęziowych należy wrócić do obwodu pierwotnego ze sprzężeniami magnetycznymi. Napięcia na elementach sprzężonych obliczać należy uwzględniając sprzężenia między cewkami przy wykorzystaniu wzorów | '''Schemat obwodu po eliminacji sprzężeń jest równoważny obwodowi oryginalnemu jedynie pod względem prądowym.''' Stąd obwód taki może służyć wyłącznie obliczeniu prądów. Dla wyznaczenia napięć gałęziowych należy wrócić do obwodu pierwotnego ze sprzężeniami magnetycznymi. Napięcia na elementach sprzężonych obliczać należy uwzględniając sprzężenia między cewkami przy wykorzystaniu wzorów | ||
|} | |} | ||
| Linia 167: | Linia 161: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd12.png]] | ||
|valign="top"| | |valign="top"|Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym. | ||
Przyjąć następujące wartości parametrów elementów obwodu: <math>R=5\Omega, L1=2H, L2=2H, M=1H</math> oraz <math>i(t)=5sin(t+45^o)A</math>. | Przyjąć następujące wartości parametrów elementów obwodu: <math>R=5\Omega, L1=2H, L2=2H, M=1H</math> oraz <math>i(t)=5sin(t+45^o)A</math>. | ||
| Linia 178: | Linia 170: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd13.png]] | ||
|valign="top"| | |valign="top"|Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzieprzedstawia postać obwodu po eliminacji sprzężenia magnetycznego. | ||
|} | |} | ||
Wersja z 12:48, 24 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
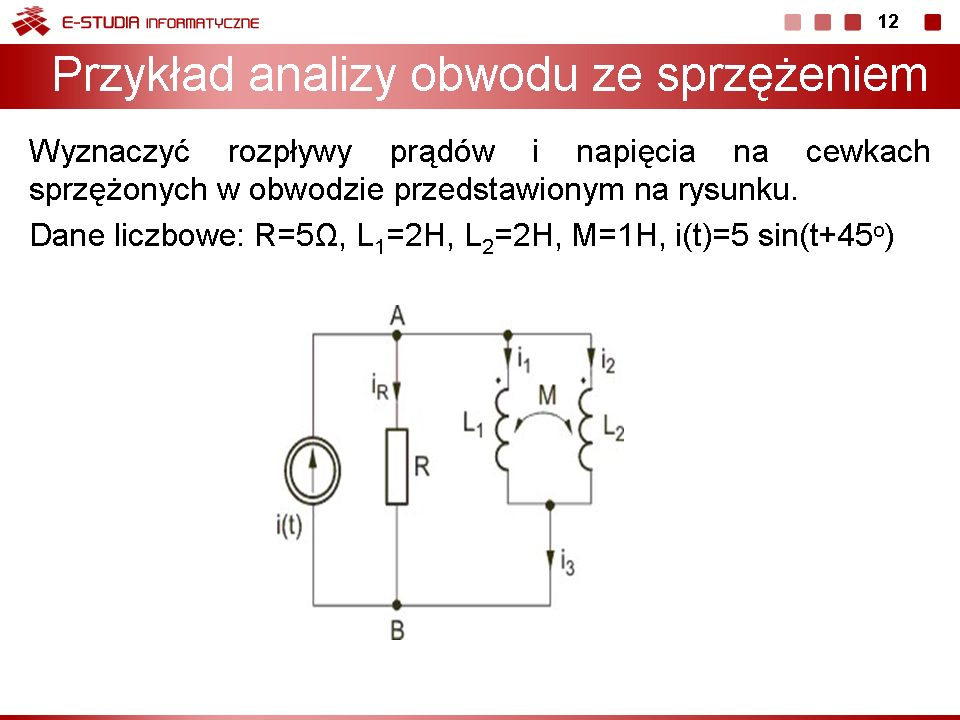
Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym.
Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzieprzedstawia postać obwodu po eliminacji sprzężenia magnetycznego. |

|
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
|

|
PRZYKŁAD
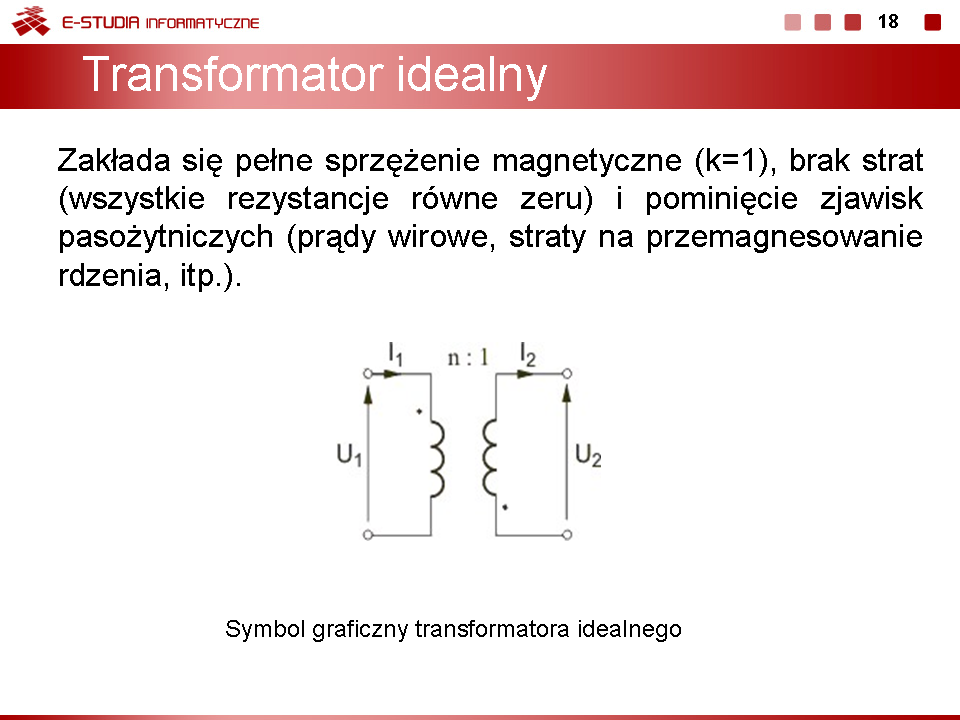
Wyznaczyć rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej . Przyjąć następujące wartości parametrów obwodu: |

|
Rozwiązanie
Wielkości symboliczne charakteryzujące elementy obwodu:
|

|
Po wstawieniu wartości liczbowych otrzymuje się
Po uproszczeniu tego układu równań otrzymuje się
Stąd
Łatwo sprawdzić, że stosunek prądu do prądu podczas gdy
|