PEE Moduł 5

Wykład 5. Obwody ze sprzężeniami magnetycznymi

---

Zjawiska fizyczne przy sprzężeniu magnetycznym cewek Przyjmijmy, że dwie cewki są położone blisko siebie w taki sposób, że strumień magnetyczny jednej cewki przenika również drugą. Całkowity strumień skojarzony z daną cewką (strumień skojarzony jest sumą strumieni $\varphi$ każdego zwoju cewki, co przy z zwojach o identycznym strumieniu daje $\psi =z\varphi$ jest wtedy sumą obu strumieni, jeśli ich kierunki są zgodne lub ich różnicą, jeśli kierunki strumieni są przeciwne. Strumienie obu cewek zapiszemy wówczas w postaci. ${\psi }_1={\psi }_1{}_1\pm {\psi }_1{}_2$ ${\psi }_2={\psi }_2{}_2\pm {\psi }_2{}_1$

---

Strumień ${\psi }_1{}_1$ występujący w cewce pierwszej pochodzi od prądu tej cewki a strumień jest wytworzony przez cewkę drugą i przenika przez cewkę pierwszą. Podobnie strumień ${\psi }_2{}_2$ pojawiający się w cewce drugiej pochodzi od prądu tej cewki a strumień pochodzący od prądu cewki pierwszej przenika przez cewkę drugą. Uwzględniając pojęcie indukcyjności własnej i wzajemnej wprowadzone w rozdziale pierwszym dla cewek liniowych sprzężonych magnetycznie obowiązują następujące relacje: Indukcyjności własne $L_1=\frac{{\psi }_{11}}{i_1}$, $L_2=\frac{{\psi }_{22}}{i_2}$ Indukcyjności wzajemne $M_{12}=\frac{{\psi }_{12}}{i_2}$, $M_{21}=\frac{{\psi }_{21}}{i_1}$ Dla środowisk o tej samej przenikalności magnetycznej obie indukcyjności wzajemne są sobie równe, to znaczy $M_1{}_2=M_2{}_1=M$ Dla dwu cewek sprzężonych magnetycznie definiuje się współczynnik sprzężenia jako średnią geometryczną współczynników sprzężenia obu cewek, przy czym współczynnik sprzężenia jednej cewki z drugą jest określany jako stosunek strumienia głównego cewki pochodzącego od prądu własnego do strumienia całkowitego cewki. Współczynnik sprzężenia cewek oznaczać będziemy literą $k$. Spełnia on następującą relację $M=k\sqrt{L_1{L}_2}$ Przy idealnym (pełnym) sprzężeniu cewek wartość współczynnika sprzężenia jest równa jeden (k=1). Indukcyjność wzajemna jest wówczas średnią geometryczną indukcyjności własnych obu cewek. Przy braku sprzężenia magnetycznego między cewkami wartość k=0.

---

Sprzężenie magnetyczne powoduje indukowanie się napięcia w cewce od zmian prądu własnego cewki i od zmian prądu cewki z nią sprzężonej. Wzory określające odpowiednie napięcia na cewkach sprzężonych magnetycznie dane są wówczas w postaci $u_1=\frac{d{\psi }_1}{dt}=L_1\frac{d{i}_1}{dt}\pm M\frac{d{i}_2}{dt}$ $u_2=\frac{d{\psi }_2}{dt}=L_2\frac{d{i}_2}{dt}\pm M\frac{d{i}_1}{dt}$ Znak plus lub minus występujący we wzorze odpowiada sprzężeniu bądź dodatniemu (znak plus) bądź ujemnemu (znak minus). Rodzaj sprzężenia zależy od kierunku prądu cewki względem początku uzwojenia. 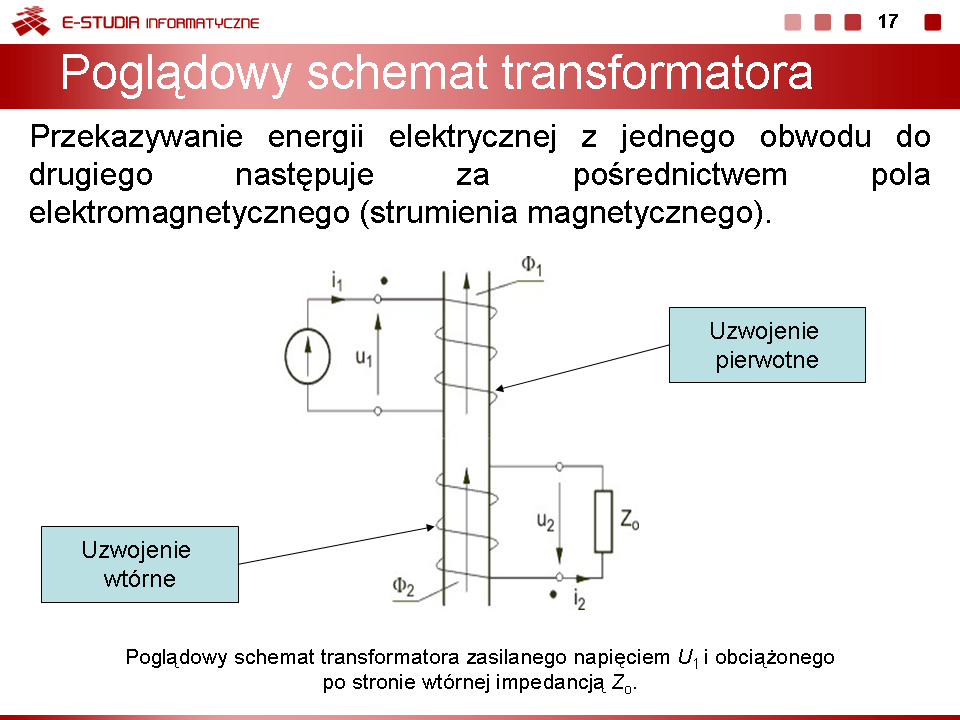Zauważmy, że przy istnieniu sprzężenia magnetycznego w cewce generowane jest napięcie na cewce nawet przy prądzie własnym cewki równym zeru. Oznacza to przenoszenie się energii z jednego obwodu do drugiego drogą magnetyczną.

---

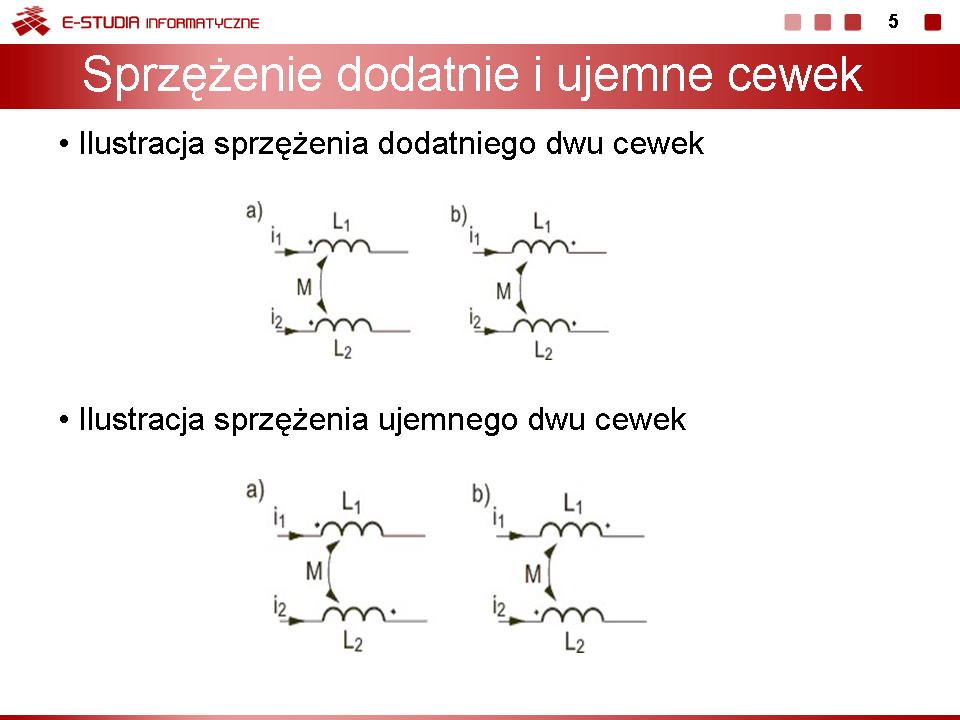
Rysunek obok ilustruje schematyczne oznaczenia sprzężenia dodatniego i ujemnego dwóch cewek. Sprzeżenie jest dodatnie, jeśli kierunki prądów w obu cewkach są jednakowo usytuowane względem początków uzwojeń cewek. Sprzeżenie jest ujemne, jeśli kierunki prądów w cewkach są przeciwnie usytuowane względem początków uzwojeń tych cewek.

---

---

Równania symboliczne elementów sprzężonych magnetycznie Analiza obwodów ze sprzężeniami magnetycznymi w stanie ustalonym przy wymuszeniu sinusoidalnym może być przeprowadzona przy zastosowaniu metody symbolicznej, w której w miejsce różniczkowania wprowadza się działania na liczbach zespolonych. Dla wymuszenia sinusoidalnego wzory różniczkowe upraszczają się do zależności algebraicznych typu zespolonego, które podobnie jak dla indukcyjności własnych wyprowadzonych w rozdziale drugim można zapisać w postaci Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle U_1=j\omega L_1I_1\pm j\omeha MI_2} Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle U_2=j\omega L_2I_2\pm j\omeha MI_1} Znak plus obowiązuje dla sprzężenia dodatniego (strumienie magnetyczne obu cewek sumują się) a znak minus dla sprzężenia ujemnego (strumienie magnetyczne obu cewek odejmują się). Jak widać z powyższych wzorów cewki sprzężone magnetycznie reprezentują sobą reaktancje, przy czym można tu wyróżnić dwa rodzaje reaktancji: reaktancję indukcyjną własną (zwaną dotąd reaktancją indukcyjną) i reaktancję indukcyjną wzajemną. Wprowadźmy następujące oznaczenia $X_M=\omega M$ reaktancja indukcyjna wzajemna $Z_M=j\omega M$ impedancja indukcyjna wzajemna

---

Napięcie skuteczne zespolone na cewkach sprzężonych można wówczas opisać następującymi wzorami $U_1=Z_{L1}{I}_1\pm Z_M{I}_2=j\omega L_1{I}_1\pm j\omega M{I}_2$ $U_2=Z_{L1}{I}_2\pm Z_M{I}_1=j\omega L_2{I}_2\pm j\omega M{I}_1$ w których $Z_{L1}$ oraz $Z_{L2}$ oznaczają impedancje indukcyjności własnych cewki pierwszej i drugiej, $Z_{L1}=j\omega L_1,Z_{L2}=j\omega L_2$ , . Dla wyznaczenia wartości skutecznej napięcia na cewce sprzężonej muszą być znane zarówno wartości skuteczne prądu jednej cewki jak i drugiej, sprzężonej z nią. Znak sprzężenia (plus lub minus) powoduje odejmowanie (sprzężenie ujemne) lub dodawanie (sprzężenie dodatnie) napięć pochodzących od sprzężenia.

---

Najważniejszym elementem analizy obwodów ze sprzężeniami magnetycznymi jest wyznaczenie prądów poszczególnych gałęzi w obwodzie. Bezpośrednie zastosowanie poznanych dotąd metod analizy obwodów (metoda węzłowa, oczkowa, Thevenina czy Nortona) wymaga w pierwszej kolejności wyeliminowania sprzężenia magnetycznego cewek, a więc pozbycia się wpływu prądu jednej cewki na napięcie cewki drugiej Eliminacja sprzężeń magnetycznych Eliminacja sprzężeń magnetycznych jest możliwa bezpośrednio na podstawie analizy struktury obwodu i uwzględnienia położenia początków uzwojeń cewek względem węzłów wspólnych (lub uznanych za wspólne przy braku ich bezpośredniego połączenia). W tym przypadku można wyróżnić dwa rodzaje połączeń: dwie cewki sprzężone magnetycznie mają jednakowo usytuowane początki uzwojeń względem węzła - takie cewki uważać będziemy za jednoimienne dwie cewki sprzężone magnetycznie mają przeciwnie usytuowane początki uzwojeń względem węzła - takie cewki uważać będziemy za różnoimienne.

---

---

W przypadku cewek jednoimiennych eliminacja sprzężenia magnetycznego prowadzi do obwodu zastępczego przedstawionego na rysunku W gałęziach zawierających cewki pojawiła się impedancja wzajemna ze znakiem minus a w gałęzi wspólnej impedancja wzajemna ze znakiem plus. Łatwo można pokazać, że przy takim sposobie eliminacji sprzężeń magnetycznych napięcia na zaciskach zewnętrznych 1, 2 i 3 przy niezmienionych prądach zewnętrznych w obu obwodach równają się sobie (co jest warunkiem równoważności). W gałęziach zawierających cewki pojawiła się impedancja wzajemna ze znakiem plus a w gałęzi wspólnej impedancja wzajemna ze znakiem minus. Łatwo udowodnić, że przy takim sposobie eliminacji sprzężeń napięcia na zaciskach zewnętrznych 1, 2 i 3 w obu obwodach (oryginalnym i po eliminacji sprzężenia) przy tych samych prądach zewnętrznych równają się sobie (co jest warunkiem równoważności). Przy eliminacji sprzężeń magnetycznych przyjęty zwrot prądów nie ma żadnego wpływu na końcową postać obwodu bez sprzężeń. Ma na nią wpływ jedynie usytuowanie początków uzwojeń cewek względem wspólnego węzła, czyli jednoimienność lub różnoimienność cewek sprzężonych magnetycznie. W obu przypadkach otrzymuje się obwody bez sprzężeń, równoważne oryginalnym jedynie pod względem prądowym. Napięcia w obu obwodach w części podlegającej przekształceniu są całkowicie różne. Rzeczywiste napięcia panujące na elementach podlegających transformacji powinny być określane bezpośrednio na podstawie obwodu oryginalnego i powinny uwzględniać sprzężenie magnetyczne Należy podkreślić, że przy wielu cewkach sprzężonych ze sobą, eliminacja każdego sprzężenia między dwoma wybranymi cewkami może zachodzić niezależnie od pozostałych sprzężeń, co znakomicie ułatwia przeprowadzenie procesu eliminacji sprzężeń.

---

Przykład 5.1 Na rysunku przedstawiony jest obwód zawierający trzy cewki sprzężone magnetycznie ze sobą. Stosując metodę eliminacji sprzężeń do każdej pary cewek sprzężonych ze sobą otrzymuje się schemat obwodu bez sprzężeń, równoważny pod względem prądowym obwodowi ze sprzężeniami Przy analizie obwodów elektrycznych zawierających sprzężenia magnetyczne pierwszym krokiem jest eliminacja sprzężeń magnetycznych zgodnie z zasadami podanymi wyżej. Dzięki temu każdy element obwodu staje się uzależniony jedynie od swojego prądu. Schemat obwodu po eliminacji sprzężeń jest równoważny obwodowi oryginalnemu jedynie pod względem prądowym. Stąd obwód taki może służyć wyłącznie obliczeniu prądów. Dla wyznaczenia napięć gałęziowych należy wrócić do obwodu pierwotnego ze sprzężeniami magnetycznymi. Napięcia na elementach sprzężonych obliczać należy uwzględniając sprzężenia między cewkami przy wykorzystaniu wzorów Przykład eliminacji sprzężeń magnetycznych wielu cewek: a) obwód oryginalny, b) obwód po eliminacji sprzężeń

---

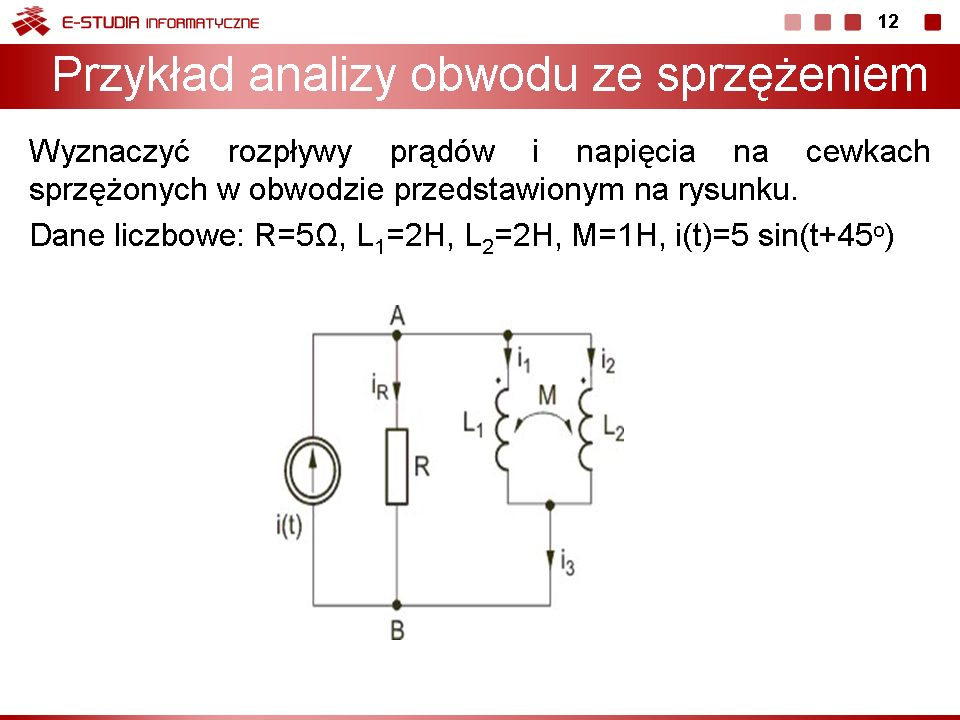
PRZYKŁAD Wyznaczyć rozpływy prądów w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów elementów obwodu: $R=5\mathrm{\Omega },L1=2H,L2=2H,M=1H$ oraz $i(t)=5sin(t+45^o)A$.

---

Rozwiązanie Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku

---

Wielkości symboliczne charakteryzujące elementy obwodu: $I=\frac{5}{\sqrt{2}}{e}^{j45^o}$ $Z_1=j\omega (L_1-M)=j1$ $Z_2=j\omega (L_2-M)=0$ $Z_M=j\omega M=j1$ Impedancja zastępcza obwodu wobec $Z_2=0$ $Z=\frac{R{Z}_M}{R+Z_M}=\frac{1}{\sqrt{2}}{e}^{j45^o}$

---

Napięcie $U_A{}_B$ $U_{AB}=ZI=j5$ Prądy: $I_R=\frac{U_{AB}}{R}=j5$ $I_1=0$ $I_2=I_3\frac{U_{AB}}{Z_M}=5$ Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą $U_{AB}=j5$ Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie $U_{L_1}=j\omega L_1{I}_1+j\omega M{I}_2=j5$ $U_{L_2}=j\omega L_2{I}_2+j\omega M{I}_1=j5$

---

Transformator Podstawy fizyczne działania transformatora Transformator jest układem przetwarzającym napięcie wejściowe w napięcie wyjściowe za pośrednictwem strumienia magnetycznego przy braku bezpośredniego połączenia galwanicznego między obu zaciskami (wejściowymi i wyjściowymi). Transformatory mogą być stosowane do różnych celów, ale podstawowym ich zadaniem jest zmiana wartości napięcia wejściowego na inną wartość napięcia wyjściowego. Może to być zarówno podwyższenie jak i obniżenie wartości. Przy zmianie napięcia ulegają odpowiedniej zmianie również prądy w uzwojeniach transformatora. W analizie teoretycznej przyjmować będziemy transformator idealizowany, czyli taki w którym nie ma strat energii, nie istnieje zjawisko rozpraszania strumienia magnetycznego (współczynnik sprzężenia magnetycznego k=1), nie występują efekty pasożytnicze (np. pojemności międzyzwojowe), nie uwzględniona jest rezystancja uzwojeń, zjawiska prądów wirowych itp.

---

Przekazywanie energii elektrycznej z jednego obwodu do drugiego następuje za pośrednictwem pola elektromagnetycznego (strumienia magnetycznego). Na rysunku przedstawiono poglądowy schemat transformatora zasilanego napięciem $U_1$ i obciążonego po stronie wtórnej impedancją $Z_o$. Uzwojenie, do którego jest zazwyczaj doprowadzone źródło energii elektrycznej, nazywamy uzwojeniem pierwotnym, natomiast uzwojenie, do którego jest dołączony odbiornik, nazywamy uzwojeniem wtórnym. Zaciski uzwojenia pierwotnego stanowią wejście układu, a zaciski uzwojenia wtórnego - wyjście. Odpowiednie napięcia i prądy w transformatorze nazywamy pierwotnymi lub wtórnymi. Wszystkie wielkości i parametry związane z uzwojeniem pierwotnym opatrzymy wskaźnikiem 1, a wielkości i parametry związane z uzwojeniem wtórnym – wskaźnikiem 2. Do uzwojenia pierwotnego przyłożone jest napięcie sinusoidalnie zmienne o wartości chwilowej $u_1(t)$. Wartość chwilową prądu w uzwojeniu pierwotnym oznaczymy przez $i_1(t)$ Pod wpływem zmiennego w czasie prądu $i_1(t)$ w przestrzeni otaczającej uzwojenie powstaje zmienny strumień magnetyczny $\varphi$ , będący superpozycją strumieni ${\varphi }_{1}i{\varphi }_2$ . Przy założeniu jego równomiernego rozkładu na przekroju S, strumień jest iloczynem indukcji magnetycznej B i przekroju S,$\varphi =BS$ Strumień ten kojarzy się zarówno z uzwojeniem pierwotnym o liczbie zwojów $z_1$ wytwarzając strumień skojarzony ${\psi }_1=z_1\varphi$, jak i uzwojeniem wtórnym o liczbie zwojów z2 wytwarzając w nim strumień skojarzony ${\psi }_2=z_2\varphi$ Zgodne z prawem indukcji elektromagnetycznej pod wpływem zmiennego w czasie strumienia magnetycznego indukuje się napięcie$u(t)$ $u(t)\frac{d\psi }{dt}$ Jeśli do uzwojenia wtórnego dołączymy odbiornik, to pod wpływem napięcia indukowanego w tym uzwojeniu popłynie prąd $i_2(t)$. W zależności od środowiska w jakim zamyka się wytworzony wokół uzwojeń strumień magnetyczny rozróżniamy transformatory powietrzne (korpus transformatora wykonany z dielektryka o przenikalności magnetycznej względnej bliskiej jedności) i transformatory z rdzeniem ferromagnetycznym (korpus wykonany z rdzenia ferromagnetycznego). Zanim przejdziemy do omówienia obu rodzajów transformatorów, przedstawimy zależności obowiązujące dla transformatora idealnego.

---

Transformator idealny Wyidealizowanym typem transformatora jest tak zwany transformator idealny, w którym zakłada się pełne sprzężenie magnetyczne (k=1), brak strat (wszystkie rezystancje równe zeru) i pominięcie zjawisk pasożytniczych. Symbol graficzny transformatora idealnego przedstawiono na rysunku. W schemacie tym pomija się zwykle symbol sprzężenia magnetycznego pozostawiając jedynie oznaczenie początków uzwojeń transformatora.

---

Transformator idealny jest w pełni opisany poprzez tak zwaną przekładnię zwojową, określającą stosunek napięcia pierwotnego do wtórnego (przekładnię napięciową) na podstawie liczby zwojów pierwotnych i wtórnych. Przekładnia napięciowa transformatora idealnego niezależnie od sposobu wykonania i od obciążenia, powinna być równa przekładni zwojowej określonej wzorem $n=\frac{z_1}{z_2}$ Oznacza to, że relacja między napięciem pierwotnym i wtórnym jest następująca $\frac{U_1}{U_2}=n\to U_1=\frac{z_1}{z_2}{U}_2$ Wobec założenia o braku strat w samym transformatorze idealnym moc dostarczona na zaciski pierwotne równa się mocy na zaciskach wtórnych, to jest $S_1=S_2$ (podobnie jest z mocą czynną i bierną). Przy oznaczeniu przekładni transformatora idealnego przez n, z warunku równości mocy wejściowej i wyjściowej, to znaczy $U_1{I}_1^{*}=U_2{I}_2^{*}$ Wynika stąd relacja między prądem pierwotnym i wtórnym transformatora. Mianowicie $I_1=\frac{1}{n}{I}_2$ Obie zależności można zapisać w następującej postaci macierzowej $\left[\begin{array}{c}{U}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}n& 0\\ 0& \frac{1}{n}\end{array}\right]\left[\begin{array}{c}{U}_2\\ I_2\end{array}\right]$ Powyższe równanie macierzowe nazywane jest równaniem łańcuchowym transformatora idealnego. Wykonanie transformatora idealnego w praktyce nie jest możliwe, jednak współczesne realizacje techniczne transformatorów zwłaszcza transformatory z rdzeniem ferromagnetycznym są bliskie ideału.

---

Realizacja transformatora w układzie cewek magnetycznie sprzężonych Transformator rzeczywisty realizuje się w układzie cewek magnetycznie sprzężonych, nawiniętych na korpusie wykonanym zwykle z materiału ferromagnetycznego, zapewniającego bliskie idealnemu sprzężenie magnetyczne (k≈1). Model idealnego transformatora magnetycznego (bez uwzględnienia rezystancji uzwojeń) obciążonego impedancją $Z_o$ jest przedstawiony na rysunku. Indukcyjności własne uzwojeń oznaczone są przez $L_{1}i{L}_2$ a indukcyjność wzajemna przez $M$, przy czym $M=k\sqrt{L_1{L}_2}$ Napięcie zasilające wywołuje w obwodzie pierwotnym prąd $I_1$, wytwarzający strumień magnetyczny. Energia obwodu pierwotnego przenosi się do obwodu wtórnego poprzez sprzężenie magnetyczne, zaznaczone symbolicznie jako indukcyjność wzajemna $M$. Pod wpływem zaindukowanego napięcia przy zamkniętym obwodzie wtórnym płynie prąd $I_2$, odkładając na impedancji odbiornika napięcie $U_2$.

---

Analizując transformator w stanie ustalonym przy wymuszeniu sinusoidalnym zastosujemy metodę symboliczną. Z definicji sprzężenia magnetycznego obu cewek przy założonym zwrocie prądów i przyjęciu początków uzwojeń jak na rysunku wynikają następujące równania opisujące obwód $U_1=j{X}_l{}_1{I}_1+j{X}_M{I}_2$ $U_2=-[j{X}_L{}_2{I}_2+j{X}_M{I}_1]$ Znak minus występujący we wzorze na $U_2$ wynika z kierunku $U_2$ zaznaczonego na rysunku Z równań wynika następujący wzór określający napięcie wyjściowe $U_2=-[\frac{X_M}{X_{L1}}{U}_1+j{I}_2(\frac{X_{L1}{X}_{L2}-X_M^2}{X_{L1}})]$ Przy założeniu wyidealizowanego transformatora $(k\approx 1)$ zachodzi $X_M^2\approx X_{L1}{X}_{L2}$ . Oznacza to, że niezależnie od obciążenia relacja między napięciem pierwotnym i wtórnym dana jest w postaci $U_2\approx -\frac{X_M}{X_{L1}}{U}_1$

---

Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji $X_{L1}=K{z}_1^2,X_{L2}=K{z}_2^2,X_M=K{z}_1{z}_2$ gdzie K oznacza pewną stałą konstrukcyjną, to z zależności wynika $\frac{U_2}{U_1}=-\frac{z_2}{z_1}=-\frac{1}{n}$ Napięcie wtórne transformatora jest zależne wyłącznie od przekładni zwojowej i napięcia wejściowego układu (znak minus nie odgrywa żadnej roli a jedynie oznacza przesunięcie fazowe $180^o$ napięcia wyjściowego względem wejściowego). Jest to zatem realizacja podstawowej zależności charakterystycznej dla transformatora idealnego. Przy pominięciu strat w transformatorze moc na wejściu równa się mocy wyjściowej, stąd relacja między prądem pierwotnym i wtórnym spełnia również drugą zależność transformatora idealnego ). Wynika stąd wniosek, że transformator z rdzeniem ferromagnetycznym jest dobrym przybliżeniem transformatora idealnego.

---

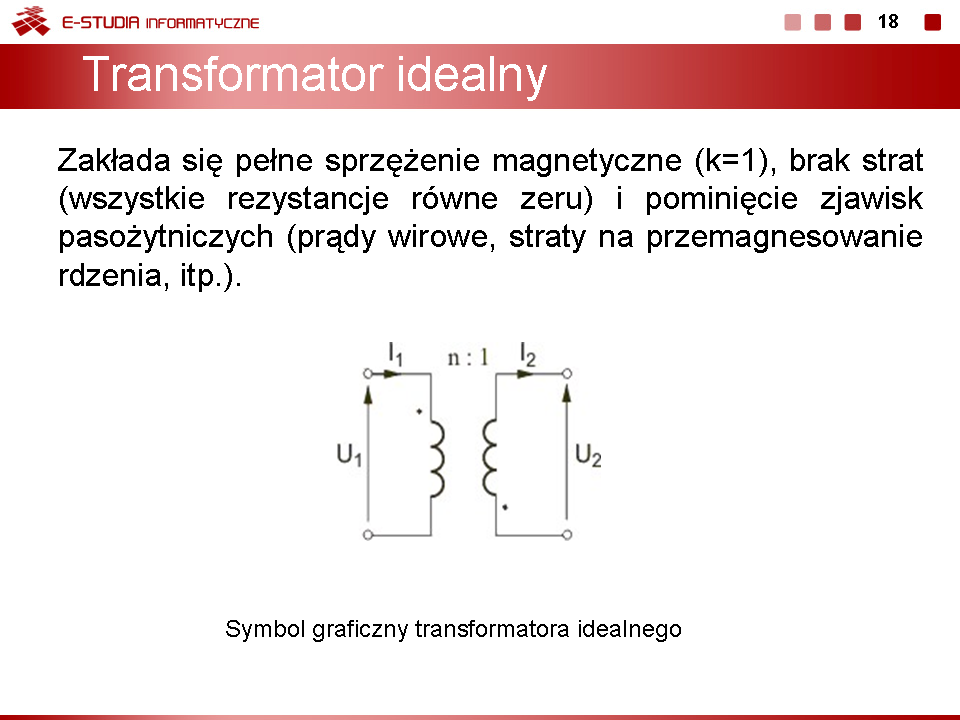
PRZYKŁAD Wyznaczyć rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej $n=2$. Przyjąć następujące wartości parametrów obwodu: $e(t)=10\sqrt{2}sin(\omega t)V,\omega =1rad/s,R=5\mathrm{\Omega },C=0,2F$

---

Rozwiązanie Wielkości symboliczne charakteryzujące elementy obwodu: $E=10$ $Z_C=-\frac{j}{\omega C}=-j5$ $Z_R{}_C=\frac{R{Z}_C}{R_Z{}_C}=2,5-j2,5$ Układ równań opisujących obwód: $E=R{I}_1+U_1$ $U_1=n{U}_2$ $I_1=\frac{1}{n}{I}_2$ $U_2=I_2{Z}_{RC}$

---

Po wstawieniu wartości liczbowych otrzymuje się $10=5I_1+U_1$ $U_1=2U_2$ $I_1=\frac{1}{2}{I}_2$ $U_2=I_2(2,5-j2,5)$ Po uproszczeniu tego układu równań otrzymuje się $10=(5+10\sqrt{2}{e}^{-j45^o})I_1$ Stąd $I_1=0,45+j0,30$ $I_2=2I_1=0,90+j0,60$ $U_2=Z_{RC}{I}_2=3,79-j0,75$ $U_1=2U_2=758-j1,5$ $I_3=\frac{U_2}{R}=0,75-j0,15$ $I_4=\frac{U_2}{Z_C}=0,15+j0,76$ Łatwo sprawdzić, że stosunek prądu $I_1$ do prądu $I_2,\frac{I_1}{I_2}=\frac{1}{2}$ podczas gdy $\frac{U_1}{U_2}=2$

---