PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 25: | Linia 25: | ||
*Indukcyjności własne | *Indukcyjności własne | ||
<math>L_1=\frac{\psi_{11}}{i_1}</math>, <math>L_2=\frac{\psi_{22}}{i_2}</math> | |||
<math>L_1=\frac{\ | |||
<math>L_2=\frac{\ | |||
*Indukcyjności wzajemne | *Indukcyjności wzajemne | ||
<math>M_{12}=\frac{\psi_{12}}{i_2}</math>, <math>M_{21}=\frac{\psi_{21}}{i_1}</math> | |||
<math> | |||
<math> | |||
| Linia 58: | Linia 50: | ||
<math>u_1=\frac{d\psi_1}{dt} | <math>u_1=\frac{d\psi_1}{dt} = L_1\frac{di_1}{dt}\pm M\frac{di_2}{dt}</math> | ||
<math>u_2=\frac{d\psi_2}{dt} | <math>u_2=\frac{d\psi_2}{dt} = L_2\frac{di_2}{dt}\pm M\frac{di_1}{dt}</math> | ||
| Linia 81: | Linia 73: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd6.png]] | ||
|valign="top"| | |valign="top"|'''Równania symboliczne elementów sprzężonych magnetycznie''' | ||
'''Równania symboliczne elementów sprzężonych magnetycznie''' | |||
Analiza obwodów ze sprzężeniami magnetycznymi w stanie ustalonym przy wymuszeniu sinusoidalnym może być przeprowadzona przy zastosowaniu metody symbolicznej, w której w miejsce różniczkowania wprowadza się działania na liczbach zespolonych. Dla wymuszenia sinusoidalnego wzory różniczkowe upraszczają się do zależności algebraicznych typu zespolonego, które podobnie jak dla indukcyjności własnych wyprowadzonych w rozdziale drugim można zapisać w postaci | Analiza obwodów ze sprzężeniami magnetycznymi w stanie ustalonym przy wymuszeniu sinusoidalnym może być przeprowadzona przy zastosowaniu metody symbolicznej, w której w miejsce różniczkowania wprowadza się działania na liczbach zespolonych. Dla wymuszenia sinusoidalnego wzory różniczkowe upraszczają się do zależności algebraicznych typu zespolonego, które podobnie jak dla indukcyjności własnych wyprowadzonych w rozdziale drugim można zapisać w postaci | ||
<math>U_1=j\omega L_1I_1\pm j\omeha MI_2</math> | <math>U_1=j\omega L_1I_1\pm j\omeha MI_2</math> | ||
<math>U_2=j\omega L_2I_2\pm j\omeha MI_1</math> | <math>U_2=j\omega L_2I_2\pm j\omeha MI_1</math> | ||
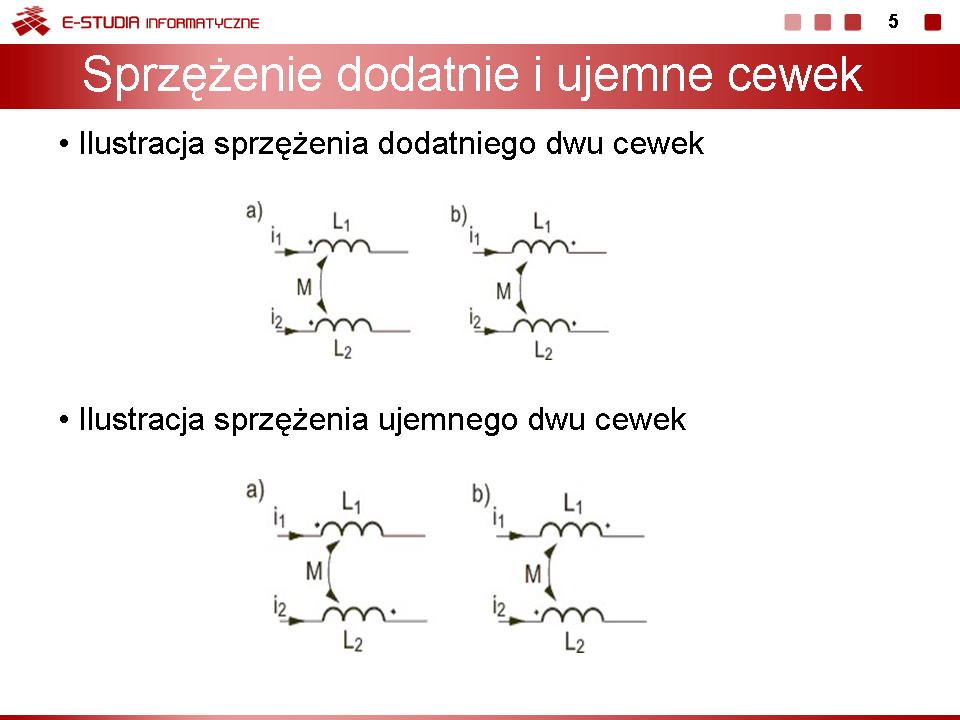
Znak plus obowiązuje dla '''sprzężenia dodatniego''' (strumienie magnetyczne obu cewek sumują się) a znak minus dla '''sprzężenia ujemnego''' (strumienie magnetyczne obu cewek odejmują się). Jak widać z powyższych wzorów cewki sprzężone magnetycznie reprezentują sobą reaktancje, przy czym można tu wyróżnić dwa rodzaje reaktancji: '''reaktancję indukcyjną własną''' (zwaną dotąd reaktancją indukcyjną) i '''reaktancję indukcyjną wzajemną'''. Wprowadźmy następujące oznaczenia | Znak plus obowiązuje dla '''sprzężenia dodatniego''' (strumienie magnetyczne obu cewek sumują się) a znak minus dla '''sprzężenia ujemnego''' (strumienie magnetyczne obu cewek odejmują się). Jak widać z powyższych wzorów cewki sprzężone magnetycznie reprezentują sobą reaktancje, przy czym można tu wyróżnić dwa rodzaje reaktancji: '''reaktancję indukcyjną własną''' (zwaną dotąd reaktancją indukcyjną) i '''reaktancję indukcyjną wzajemną'''. Wprowadźmy następujące oznaczenia | ||
<math>X_M=\omega M</math> reaktancja indukcyjna wzajemna | <math>X_M=\omega M</math> reaktancja indukcyjna wzajemna | ||
<math>Z_M=j\omega M</math> impedancja indukcyjna wzajemna | <math>Z_M=j\omega M</math> impedancja indukcyjna wzajemna | ||
Wersja z 12:25, 24 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
|
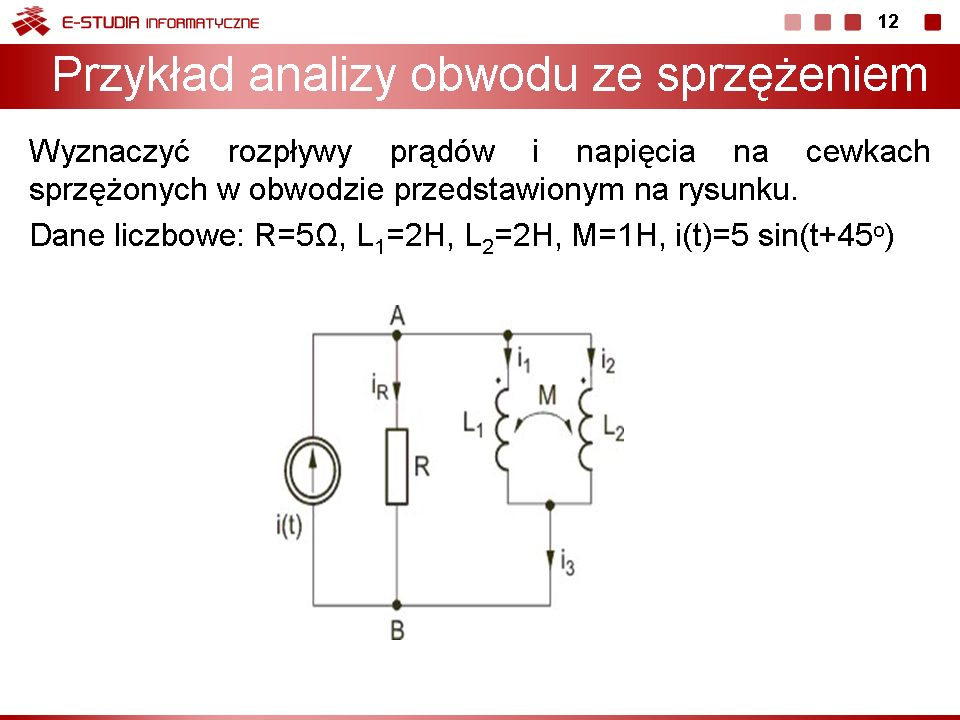
PRZYKŁAD
Wyznaczyć rozpływy prądów w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku |

|
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
|

|
PRZYKŁAD
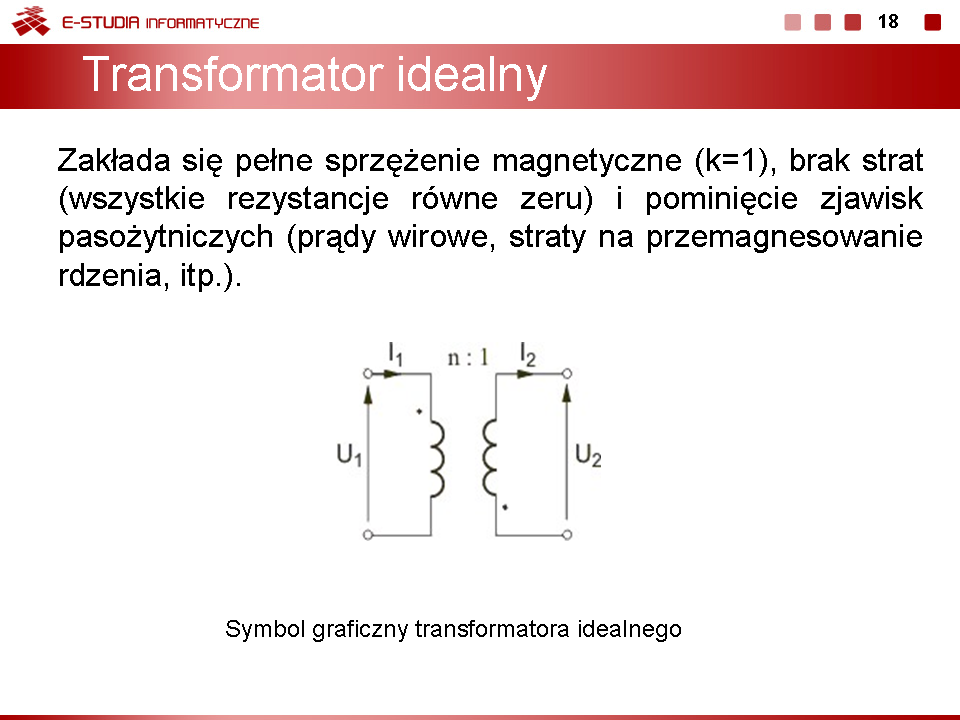
Wyznaczyć rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej . Przyjąć następujące wartości parametrów obwodu: |

|
Rozwiązanie
Wielkości symboliczne charakteryzujące elementy obwodu:
|

|
Po wstawieniu wartości liczbowych otrzymuje się
Po uproszczeniu tego układu równań otrzymuje się
Stąd
Łatwo sprawdzić, że stosunek prądu do prądu podczas gdy
|