PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 262: | Linia 262: | ||
I_{Z4}-I_{Z6}-E_5Y_5 | I_{Z4}-I_{Z6}-E_5Y_5 | ||
\end{bmatrix} | \end{bmatrix} | ||
</math>, | </math>, <math>\mathbf{V}= | ||
<math>\mathbf{V}= | |||
\begin{bmatrix} | \begin{bmatrix} | ||
V_1\\ | V_1\\ | ||
| Linia 270: | Linia 269: | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
Równanie potencjałów węzłowych obwodu | Równanie potencjałów węzłowych obwodu można zapisać w uproszczonej formie macierzowej | ||
: <math>\mathbf{YV}=\mathbf{I}_{zr}</math> | : <math>\mathbf{YV}=\mathbf{I}_{zr}</math> | ||
| Linia 291: | Linia 290: | ||
Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Dzięki takiemu założeniu są one bardzo proste i łatwe w stosowaniu. | Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Dzięki takiemu założeniu są one bardzo proste i łatwe w stosowaniu. | ||
W przypadku wystąpienia źródeł sterowanych | W przypadku wystąpienia źródeł sterowanych oraz idealnych źródeł napięciowych włączonych między węzłami trudno jest podać formułę ogólną pozwalającą określić zarówno macierz admitancyjną jak i wektor wymuszeń prądowych. Zasada tworzenia opisu admitancyjnego w takim przypadku korzysta bezpośrednio ze stwierdzenia, że opis admitancyjny powstaje jako uporządkowany zbiór równań wynikających z prawa prądowego Kirchhoffa, w których wszystkie prądy gałęziowe zostały wyrażone poprzez potencjały węzłowe i wartości źródeł wymuszających. Macierz admitancyjna <math>\mathbf{Y}\,</math> wynika wówczas z uporządkowania macierzowego powstałego układu równań. | ||
|} | |} | ||
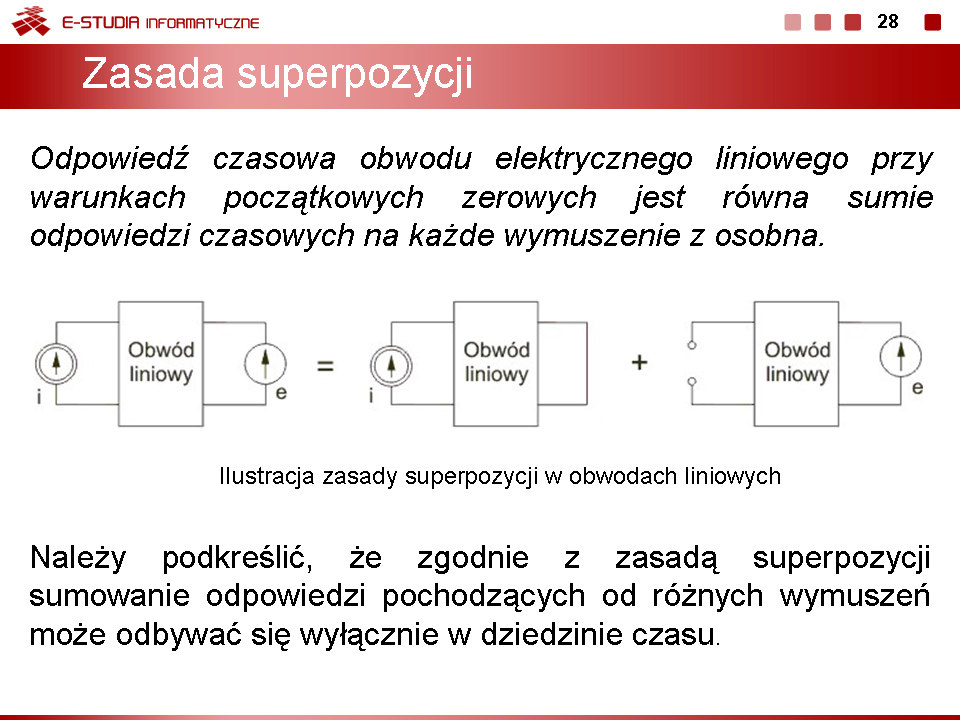
Wersja z 11:57, 24 sie 2006

|
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |

|

|

|
Przykład
Dla obwodu przedstawionego na rysunku napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. |

|
| Zadania sprawdzające
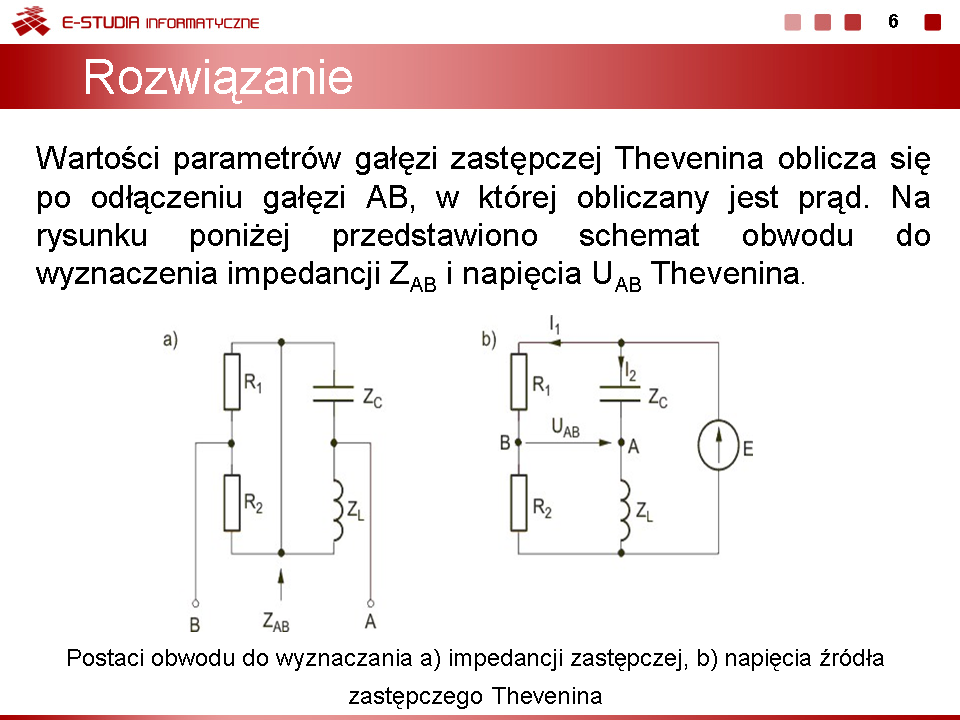
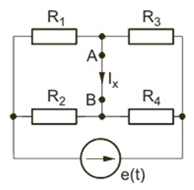
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , . Rozwiązanie Impedancja z zacisków AB obwodu jest równa
Prądy w obwodzie z rys. b:
Napięcie
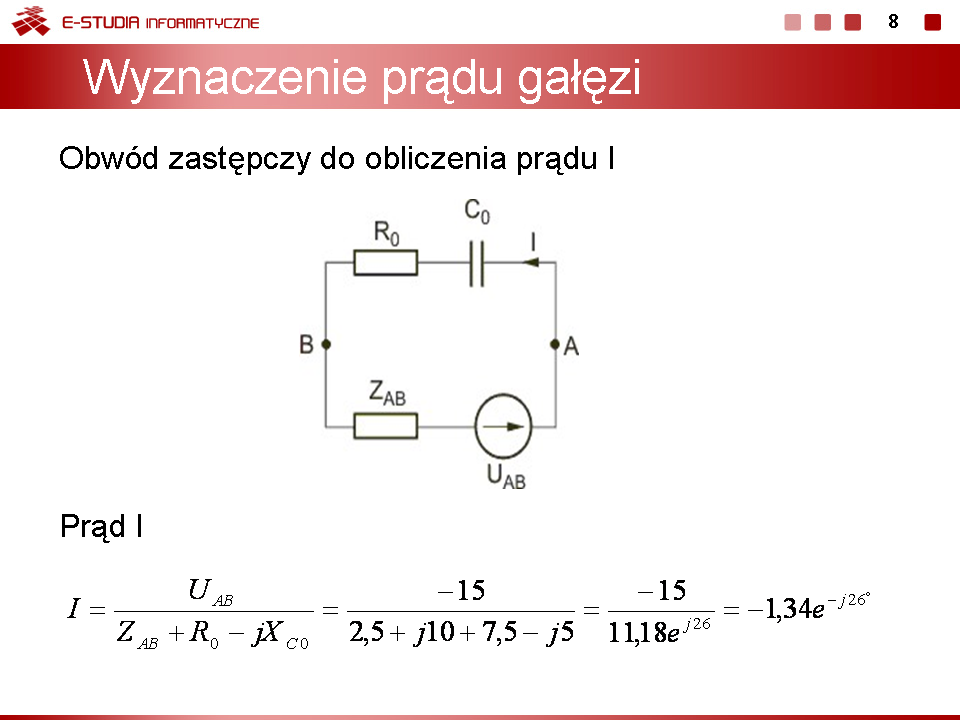
Poszukiwany prąd z obwodu zastępczego Thevenina (rys. c)
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
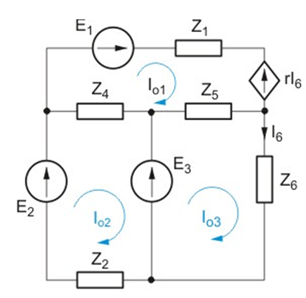
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci |