PEE Moduł 4

Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym

---

Metoda równań Kirchhoffa W metodzie tej wykorzystuje się w bezpośredniej formie prawo prądowe i napięciowe Kirchhoffa uzupełnione o równania symboliczne opisujące poszczególne elementy obwodu. W efekcie zastosowania praw Kirchhoffa otrzymuje się układ równań algebraicznych o zespolonych współczynnikach. Jeśli założymy, że obwód posiada b gałęzi i n węzłów to w równaniach opisujących obwód wykorzystuje się (n-1) równań pochodzących z prawa prądowego Kirchhoffa. Pozostałe (b-n+1) równań wynika z prawa napięciowego Kirchhoffa dla (b-n+1) dowolnie wybranych oczek niezależnych w obwodzie (oczka uważa się za niezależne, jeśli równania napięciowe opisujące je są od siebie niezależne).

---

Metoda oparta na twierdzeniu Thevenina Jednym z ważniejszych twierdzeń w teorii obwodów jest twierdzenie Thevenina. Pozwala ono zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem szeregowym jednej impedancji zastępczej oraz źródła napięciowego. Umożliwia znaczne uproszczenie struktury obwodu, a w następstwie w bardzo prosty sposób wyznaczyć prąd lub napięcie jednej wybranej gałęzi obwodu. Twierdzenie Thevenina Dowolny, aktywny obwód liniowy można zastąpić od strony wybranych zacisków gałęzi AB uproszczonym obwodem równoważnym, złożonym z szeregowego połączenia jednego idealnego źródła napięcia i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się na podstawie analizy obwodu oryginalnego jako napięcie panujące na zaciskach AB po odłączeniu gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu.

---

Na rysunku obok (slajd 4) przedstawiono sposób transformacji obwodu zgodnie z twierdzeniem Thevenina ułatwiający obliczenie prądu w wybranej gałęzi AB obwodu. Prąd $I$ występujący w gałęzi AB obwodu oryginalnego jest równy prądowi $I$ w tej samej gałęzi obwodu uproszczonego. Napięcie $U_{AB}$ występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja $Z_{AB}$ jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB w której obliczamy prąd reprezentowana jest przez impedancję $Z$, prąd tej gałęzi można obliczyć korzystając z prawa napięciowego Kirchhoffa z którego wynika wyrażenie na prąd gałęzi w następującej postaci $I=\frac{U_{AB}}{Z+Z_{AB}}$ Metoda Thevenina w większości przypadków znakomicie upraszcza analizę obwodu. Jest szczególnie użyteczna w przypadkach, w których trzeba wyznaczyć tylko jeden prąd w obwodzie, gdyż można dokonać tego bez konieczności rozwiązywania układu równań algebraicznych lub przy znacznej redukcji liczby tych równań.

---

Jako przykład rozpatrzymy obliczenie prądu w gałęzi AB obwodu przedstawionego na slajdzie. Twierdzenie Thevenina jest tu wyjątkowo użyteczne, gdyż pozwala wyznaczyć wybrany prąd obwodu bez konieczności analizy całego obwodu.

---

W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: $Z_{AB}$ i $U_{AB}$. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. Obliczenie impedancji zastępczej $Z_{AB}$ (rysunek a) wymaga wyeliminowania źródeł wymuszających w obwodzie (zwarcie źródła napięciowego). Obliczenie napięcia $U_{AB}$ (rysuenk b) wymaga jedynie wyeliminowania gałęzi AB bez jakiejkolwiek zmiany w pozostałej części obwodu.

---

Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa $Z_{AB}=\frac{R_1{R}_2}{R_1+R_2}+\frac{Z_L{Z}_C}{Z_L+Z_C}=\frac{5\cdot 5}{5+5}+\frac{j5\cdot (-j10)}{j5-j10}=2,5+j10$ Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego $U_{AB}$ w schemacie zastępczym Thevenina. Obliczając kolejno prądy $I_1=\frac{E}{R_1+R_2}=1$ $I_2=\frac{E}{j{X}_L-j{X}_C}=2j$ Napięcie $U_{AB}$ określa się ze wzoru $U_{AB}=R_1{I}_1-Z_C{I}_2=-15$

---

Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu $I$ określa się ze wzoru $I=\frac{U_{AB}}{Z_{AB}+R_0-j{X}_{C0}}=\frac{-15}{2,5+j10+7,5-j5}=\frac{-15}{11,18e^{j26^{\circ }}}=-1,34e^{-j26^{\circ }}$ Wartości chwilowe prądu $i(t)$ wyznaczane są z zależności $i(t)=-1,34\sqrt{2}sin(\omega t-26^{\circ })A$ Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych.

---

Metoda oparta na twierdzeniu Nortona Twierdzenie Nortona pozwala zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem równoległym jednej impedancji zastępczej oraz idealnego źródła prądowego. Twierdzenie Nortona Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina.

---

Rysunek na slajdzie 10 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona. Prąd $I$ oraz napięcie $U$ występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi $I$ oraz napięciu $U$ w tej samej gałęzi obwodu uproszczonego. Źródło prądowe $I_Z$ występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja $Z_{AB}$ jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB reprezentowana jest przez impedancję $Z$, napięcie tej gałęzi oblicza się z prawa prądowego Kirchhoffa $I_Z-U(\frac{1}{Z}+\frac{1}{Z_{AB}})=0$, które pozwala wyrazić poszukiwane napięcie gałęzi w postaci $U=\frac{I_Z}{1/Z+1/Z_{AB}}$ Znajomość napięcia pozwala wyznaczyć na podstawie prawa Ohma prąd gałęzi korzystając z zależności $I=U/Z$ Podobnie jak metoda Thevenina, zastosowanie twierdzenia Nortona umożliwia obliczenie prądu i napięcia tylko jednej gałęzi obwodu. Zwykle z punktu widzenia obliczeniowego wygodniejsze jest użycie metody Thevenina.

---

Równoważność twierdzenia Thevenina i Nortona Twierdzenia Thevenina i Nortona pozwalają wyznaczyć uproszczone schematy zastępcze tego samego układu elektrycznego z punktów AB obwodu wyjściowego. Oba schematy uproszczone stanowią więc obwody zastępcze równoważne sobie, co oznacza, że prąd i napięcie w gałęzi AB, która nie uległa zmianie w wyniku transformacji, są takie same. Oznacza to, że gałąź szeregowa zawierająca idealne źródło napięcia $E$ i impedancję $Z$ może być bez zmiany prądu w obwodzie zewnętrznym zastąpiona gałęzią równoległą zawierającą idealne źródło prądowe $I$ oraz impedancję $Z$, jak to zilustrowano na rysunku obok (slajd 11). Wzajemne relacje między wartościami źródła prądu i napięcia określa wzór $I=\frac{E}{Z}$ przy zamianie gałęzi szeregowej na równoległą oraz $E=ZI$ przy zamianie gałęzi równoległej na szeregową. Impedancja $Z$ w obu obwodach zastępczych pozostaje taka sama

---

Metoda potencjałów węzłowych Metoda potencjałów węzłowych, zwana również metodą węzłową, jest jedną z najogólniejszych i najczęściej stosowanych metod, pozwalających wyznaczyć prądy wszystkich gałęzi występujących w obwodzie. Jako zmienne przyjmuje się w niej potencjały poszczególnych węzłów obwodu określane względem jednego arbitralnie wybranego węzła uznanego za węzeł odniesienia („masy”), którego potencjał przyjmuje się za równy zeru. Liczba równań w tej metodzie jest równa liczbie węzłów niezależnych a więc znacznie mniejsza niż w metodzie wykorzystującej bezpośrednio układ równań otrzymanych w wyniku zastosowania praw Kirchhoffa. Metoda węzłowa wynika bezpośrednio z równań prądowych Kirchhoffa napisanych dla wszystkich węzłów niezależnych w obwodzie. Prąd każdej gałęzi obwodu jest wyrażany za pośrednictwem potencjałów węzłowych.

---

Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci $\mathbf{𝐘}\mathbf{𝐕}={\mathbf{𝐈}}_{zr}$ $\mathbf{𝐕}={\mathbf{𝐘}}^{-1}{\mathbf{𝐈}}_{zr}$ w której $\mathbf{𝐘}$, jest macierzą węzłową o wymiarach $NxN$, gdzie $N$ jest liczbą węzłów niezależnych w obwodzie, $\mathbf{𝐕}$ jest wektorem niezależnych potencjałów węzłowych o wymiarze $N$ a ${\mathbf{𝐈}}_{zr}$ jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa $\mathbf{𝐘}$, określona jest w postaci $\mathbf{𝐘}=\left[\begin{array}{cccc}{Y}_{11}& Y_{12}& \cdots & Y_{1N}\\ Y_{21}& Y_{22}& \cdots & Y_{2N}\\ \cdots & \cdots & \cdots & \cdots \\ Y_{N1}& Y_{N2}& \cdots & Y_{NN}\end{array}\right]$ a wektory $\mathbf{𝐕}$, oraz ${\mathbf{𝐈}}_{zr}$ dane są jak następuje $\mathbf{𝐕}=\left[\begin{array}{c}{V}_1\\ V_2\\ \cdots \\ V_N\end{array}\right]$, ${\mathbf{𝐈}}_{zr}=\left[\begin{array}{c}{I}_{zr1}\\ I_{zr2}\\ \cdots \\ I_{zrN}\end{array}\right]$

---

Elementy $Y_{ii}$ położone na głównej diagonalnej macierzy $\mathbf{𝐘}$ nazywane są admitancjami własnymi węzła $i$-tego. W przypadku obwodów RLC bez źródeł sterowanych admitancja własna węzła $i$-tego jest równa sumie admitancji wszystkich gałęzi włączonych w $i$-tym węźle. Elementy $Y_{ij}$ położone poza główną diagonalną są admitancjami wzajemnymi między węzłem $i$-tym oraz $j$-tym. Admitancja wzajemna dwu węzłów jest równa admitancji łączącej te węzły wziętej ze znakiem minus. Admitancja wzajemna węzła $i$-tego oraz $j$-tego jest taka sama jak węzła $j$-tego oraz $i$-tego, tzn. $Y_{ij}=Y_{ji}$. Macierz admitancyjna $\mathbf{𝐘}$ dla obwodów RLC bez źródeł sterowanych jest więc macierzą symetryczną. Elementy wektora wymuszeń prądowych ${\mathbf{𝐈}}_{zr}$ są równe sumie wszystkich prądów źródłowych wpływających do danego węzła, przy czym prąd źródłowy dopływający do węzła bierze się ze znakiem plus a prąd odpływający od węzła ze znakiem minus.

---

Podsumowując, analiza obwodów w stanie ustalonym metoda węzłową wymaga wykonania następujących etapów: Opis obwodu równaniem macierzowym potencjałów węzłowych (zmienne poszukiwane: wektor potencjałów $V$) Rozwiązanie układu równań $\mathbf{𝐕}={\mathbf{𝐘}}^{-1}{\mathbf{𝐈}}_{zr}$ Określenie prądów gałęziowych z prawa napięciowego Kirchhoffa przy znanych potencjałach węzłowych prąd gałęziowy jest równy iloczynowi admitancji elementu i napięcia na nim wyrażonego poprzez potencjały węzłowe. Należy podkreślić, że metoda potencjałów węzłowych dopuszcza istnienie w obwodzie jedynie źródeł wymuszających typu prądowego. Jeśli w obwodzie występują również źródła napięciowe należy je przekształcić w odpowiednie źródła prądowe wykorzystując do tego celu równoważność Thevenina – Nortona (patrz rys. na slajdzie nr 11).

---

Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rysunku obok. Korzystając z przedstawionych reguł formułowania równań węzłowych należy napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku.

---

Obwód zawiera 3 węzły niezależne: $V_1$, $V_2$ oraz $V_3$ mierzone względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez $Y_i$, gdzie $Y_i=1/Z_i$ otrzymuje się macierz potencjałów węzłowych $\mathbf{𝐘}$ oraz wektor prądów wymuszających ${\mathbf{𝐈}}_{zr}$ w postaci $\left[\begin{array}{ccc}{Y}_2& -Y_2& 0\\ -Y_2& Y_2+Y_3+Y_4& -Y_4\\ 0& -Y_4& Y_4+Y_5+Y_6\end{array}\right]\left[\begin{array}{c}{V}_1\\ V_2\\ V_3\end{array}\right]=\left[\begin{array}{c}{I}_{Z1}+I_{Z2}\\ E_3{Y}_3-I_{Z2}-I_{Z4}\\ I_{Z4}-I_{Z6}-E_5{Y}_5\end{array}\right]$ ${\mathbf{𝐈}}_{zr}=\left[\begin{array}{c}{I}_{Z1}+I_{Z2}\\ E_3{Y}_3-I_{Z2}-I_{Z4}\\ I_{Z4}-I_{Z6}-E_5{Y}_5\end{array}\right]$ Równanie potencjałów węzłowych obwodu przyjmuje postać $\mathbf{𝐘}\mathbf{𝐕}={\mathbf{𝐈}}_{zr}$ w której $\mathbf{𝐕}=\left[\begin{array}{c}{V}_1\\ V_2\\ V_3\end{array}\right]$

---

Na podstawie obliczonych wartości napięć węzłowych obwodu można w prosty sposób korzystając z prawa napięciowego Kirchhoffa dla poszczególnych gałęzi obwodu wyznaczyć prądy gałęziowe. Wystarczy w tym celu zastosować bądź prawo Ohma (jeśli gałąź zawiera jedynie element pasywny) lub równanie napięciowe Kirchoffa dla gałęzi szeregowej zawierającej źródło napięcia i element pasywny. Przykładowo dla obwodu z rysunku na slajdzie 16 odpowiednie zależności przyjmują postać: $I_2=Y_2(V_1-V_2)$ $I_3=Y_3(V_2-E_3)$ $I_4=Y_4(V_2-V_3)$ $I_5=Y_5(V_3+E_5)$ $I_6=Y_6{V}_3$ Należy podkreślić, że metoda potencjałów węzłowych wymaga rozwiązania układu $N$ równań, gdzie $N$ oznacza liczbę węzłów niezależnych. Zwykle liczba węzłów jest dużo mniejsza niż liczba gałęzi obwodu, stąd metoda potencjałów węzłowych jest znacznie efektywniejsza niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa. Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Dzięki takiemu założeniu są one bardzo proste i łatwe w stosowaniu. W przypadku wystąpienia źródeł sterowanych w obwodzie trudno jest podać formułę ogólną pozwalającą określić zarówno macierz admitancyjną jak i wektor wymuszeń prądowych. Zasada tworzenia opisu admitancyjnego w takim przypadku korzysta bezpośrednio ze stwierdzenia, że opis admitancyjny powstaje jako uporządkowany zbiór równań wynikających z prawa prądowego Kirchhoffa, w których wszystkie prądy gałęziowe zostały wyrażone poprzez potencjały węzłowe i wartości źródeł wymuszających. Macierz admitancyjna $Y$ wynika wówczas z uporządkowania macierzowego powstałego układu równań. Należy zwrócić uwagę na uproszczenia wynikające z istnienia w obwodzie idealnego źródła napięcia. Źródło takie ustala potencjał określonego węzła (gdy jest włączone względem węzła odniesienia) lub uzależnia potencjał jednego węzła względem drugiego (gdy jest włączone między dwoma węzłami niezależnymi). W obu przypadkach prowadzi to do redukcji liczby równań opisujących obwód.

---

---

Metoda prądów oczkowych W metodzie prądów oczkowych, zwanej również metodą oczkową, wprowadza się prądy oczkowe jako zmienne, czyli prądy przypisane niezależnym oczkom występującym w obwodzie. Przykładowy wybór oczek niezależnych i oznaczenie prądów oczkowych obwodu przedstawiono na rysunku obok (slajd 20).

---

Oznaczmy w ogólności wektor prądów oczkowych w postaci $I_0=\left[\begin{array}{c}{I}_{01}\\ I_{02}\\ \cdots \\ I_{0N}\end{array}\right]$ w której $I_{0k}$ oznacza prąd oczkowy $k$-tego oczka. Dla uzyskania opisu oczkowego wykorzystuje się prawo napięciowe Kirchhoffa napisane dla wszystkich oczek niezależnych obwodu. Następnie wyraża się wszystkie prądy gałęziowe poprzez prądy oczkowe (prąd gałęziowy jest równy sumie lub różnicy prądów oczkowych przeprowadzonych przez daną gałąź) i otrzymuje opis obwodu w postaci układu równań oczkowych $Z{I}_0=E$ gdzie macierz oczkowa $Z$ oraz wektor napięć wymuszających $E$ przyjmują postać $Z=\left[\begin{array}{cccc}{Z}_{11}& Z_{12}& \cdots & Z_{1N}\\ Z_{21}& Z_{22}& \cdots & Z_{2N}\\ \cdots & \cdots & \cdots & \cdots \\ Z_{N1}& Z_{N2}& \cdots & Z_{NN}\end{array}\right]$ $E=\left[\begin{array}{c}{E}_{01}\\ E_{02}\\ \cdots \\ E_{0N}\end{array}\right]$

---

Elementy $Z_{ii}$ położone na głównej diagonalnej macierzy $Z$ nazywamy impedancjami własnymi oczka $i$-tego. Przy założeniu, że wszystkie prądy oczkowe mają identyczny zwrot, dla obwodów RLC bez źródeł sterowanych impedancja własna oczka $i$-tego jest równa sumie impedancji wszystkich gałęzi występujących w oczku. Elementy $Z_{ij}$ położone poza główną diagonalną są impedancjami wzajemnymi między oczkiem $i$-tym oraz $j$-tym. Impedancja wzajemna dwu oczek przy identycznym zwrocie wszystkich prądów oczkowych jest równa impedancji wspólnej dla obu oczek wziętej ze znakiem minus. Impedancja wzajemna oczka $i$-tego oraz $j$-tego jest taka sama jak oczka $j$-tego oraz $i$-tego, tzn. $Z_{ij}=Z_{ji}$. Macierz $Z$ jest więc macierzą symetryczną. Element $k$-ty wektora wymuszeń napięciowych $E$ jest równy sumie wszystkich napięć źródłowych występujących w $k$-tym oczku. Przy założonej orientacji oczka napięcie źródłowe dodaje się ze znakiem plus jeśli jego zwrot jest identyczny z tą orientacją a ze znakiem minus jeśli ten zwrot jest przeciwny. Sposób tworzenia opisu oczkowego zilustrujemy na przykładzie obwodu z rysunku na slajdzie nr 24.

---

---

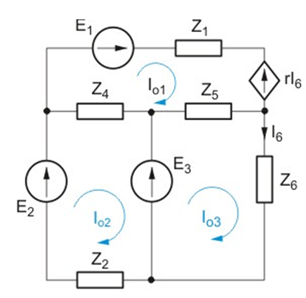
Przykład Dla obwodu przedstawionego na rysunku napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku.

---

Obwód zawiera 3 oczka niezależne, stąd wymiar macierzy oczkowej jest równy 3, podobnie jak liczba nieznanych składników wektora prądów oczkowych oraz liczba znanych składników wektora napięć wymuszających. Korzystając z podanej wcześniej reguły tworzenia opisu oczkowego otrzymuje się $Z=\left[\begin{array}{ccc}{Z}_1+Z_2+Z_3& -Z_3& -Z_1\\ -Z_3& Z_3+Z_4+Z_5& -Z_5\\ -Z_1& -Z_5& Z_1+Z_5+Z_6\end{array}\right]$ $E=\left[\begin{array}{c}-E_1-E_3\\ E_3+E_4\\ E_1-E_6\end{array}\right]$ Biorąc pod uwagę że obwód zawiera trzy nieznane prądy oczkowe tworzące wektor prądów $I_0={\left[I_{01}{I}_{02}{I}_{03}\right]}^T$, równanie oczkowe $Z{I}_0=E$ stanowi zbiór trzech równań liniowych. Rozwiązanie tego układu równań pozwala określić te zmienne. Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie

---

$I_1=I_{03}-I_{01}$ $I_2=I_{01}$ $I_3=I_{01}-I_{02}$ $I_4=I_{02}$ $I_5=I_{03}-I_{02}$ $I_6=-I_{03}$ Metoda prądów oczkowych wymaga rozwiązania układu $N$ równań, gdzie $N$ oznacza liczbę oczek niezależnych. Podobnie jak w metodzie węzłowej liczba oczek jest zwykle dużo mniejsza niż liczba gałęzi obwodu, stąd metoda prądów oczkowych jest dużo bardziej efektywna niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa.

---

---

Zasada superpozycji Omówione wcześniej metody analizy symbolicznej stanowią dobry i skuteczny sposób rozwiązania problemu przy istnieniu w obwodzie źródeł sinusoidalnych o tej samej częstotliwości, gdyż dla każdego źródła elementy reaktancyjne LC przedstawiają sobą te same wartości reaktancji. Istotna trudność występuje dopiero przy istnieniu w obwodzie wielu źródeł o różnych częstotliwościach. W takim przypadku nie istnieje pojęcie impedancji wspólnej dla każdego źródła, co uniemożliwia zastosowanie metody symbolicznej. Jedynym rozwiązaniem pozostaje wtedy zastosowanie zasady superpozycji. Obowiązuje ona tylko dla obwodów liniowych. Jej treść jest następująca. Zasada superpozycji Odpowiedź czasowa obwodu elektrycznego liniowego przy warunkach początkowych zerowych jest równa sumie odpowiedzi czasowych na każde wymuszenie z osobna. Tak ogólnie sformułowana zasada obowiązuje zarówno w stanie ustalonym jak i nieustalonym obwodu. W przypadku analizy stanów ustalonych jej zastosowanie w analizie obwodów polega na rozbiciu danego obwodu o wielu wymuszeniach na wiele obwodów zawierających po jednym wymuszeniu, rozwiązaniu każdego z nich oddzielnie a następnie zsumowaniu odpowiedzi czasowych każdego obwodu. Należy pamiętać przy tym o zasadzie, że eliminowane źródła są zastępowane zwarciem (jeśli źródło jest napięciowe) lub rozwarciem (gdy źródło jest prądowe). Należy podkreślić, że zgodnie z zasadą superpozycji sumowanie odpowiedzi pochodzących od różnych wymuszeń może odbywać się wyłącznie w dziedzinie czasu. Sumowanie wartości zespolonych od poszczególnych wymuszeń byłoby poważnym błędem, gdyż sugerowałoby istnienie rozwiązania obwodu zawierającego tylko jedną harmoniczną. Ilustrację stosowania zasady superpozycji w analizie obwodów przedstawiono na rysunku obok (slajd 28).

---

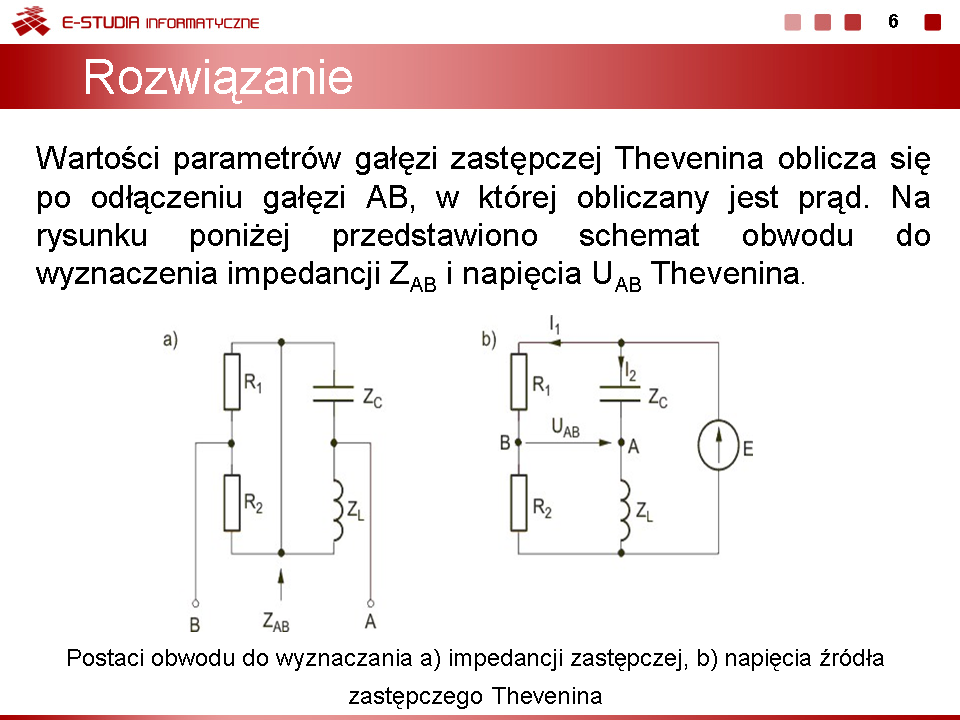
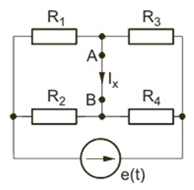
Zadania sprawdzające Zadanie 4.1 Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: $R_1=4\mathrm{\Omega }$, $R_2=8\mathrm{\Omega }$, $R_3=2\mathrm{\Omega }$, $R_4=2\mathrm{\Omega }$, $e(t)=30\sqrt{2}sin\omega tV$. Rozwiązanie Impedancja z zacisków AB obwodu jest równa $Z_{AB}=\frac{R_1{R}_3}{R_1+R_3}+\frac{R_2{R}_4}{R_2+R_4}=2,93$ Prądy w obwodzie z rys. 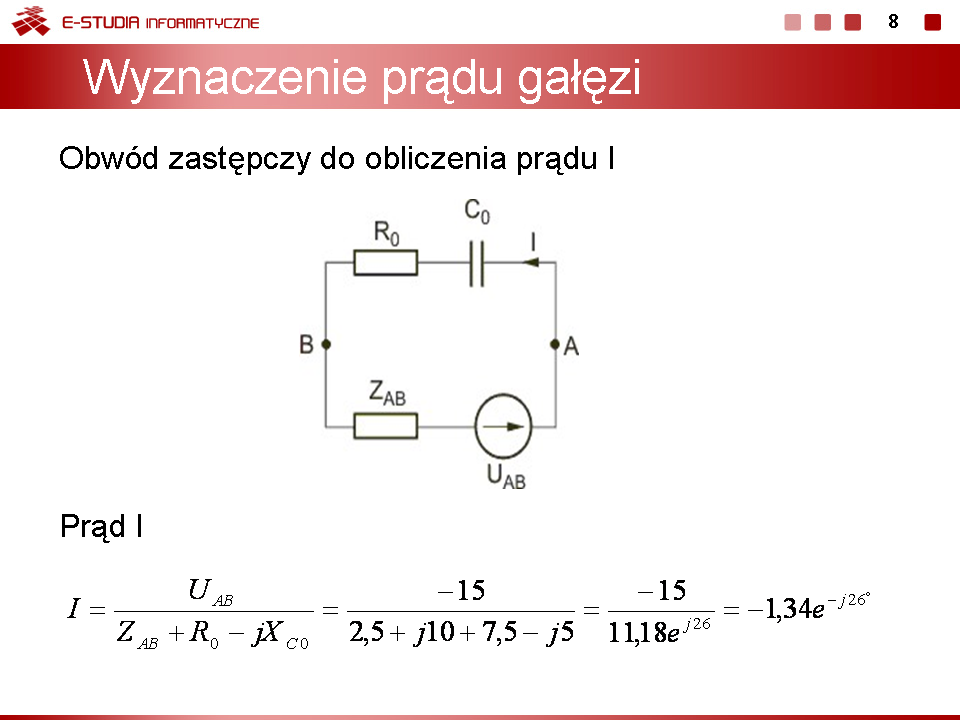b: $I_1=\frac{E}{R_1+R_3}=\frac{30}{6}=5$ $I_2=\frac{E}{R_2+R_4}=\frac{30}{10}=3$ Napięcie $U_{AB}$ $U_{AB}=R_2{I}_2-R_1{I}_1=4$ Poszukiwany prąd $I_x$ z obwodu zastępczego Thevenina (rys. c) $I_x=\frac{U_{AB}}{Z_{AB}}=1,36A$ Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci $\left[\begin{array}{ccc}{Y}_1+Y_2& -Y_2& 0\\ -Y_2& Y_2+Y_3& -Y_3+g\\ 0& -Y_3& Y_3+Y_4\end{array}\right]\left[\begin{array}{c}{V}_1\\ V_2\\ V_3\end{array}\right]=\left[\begin{array}{c}{Y}_1{E}_1-I_1\\ 0\\ -I_2\end{array}\right]$ Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci $\left[\begin{array}{ccc}{Z}_1+Z_4+Z_5& -Z_4& -Z_5+r\\ -Z_4& Z_2+Z_4& 0\\ -Z_5& 0& Z_5+Z_6\end{array}\right]\left[\begin{array}{c}{I}_{01}\\ I_{02}\\ I_{03}\end{array}\right]=\left[\begin{array}{c}{E}_1\\ E_2-E_3\\ E_3\end{array}\right]$