PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 73: | Linia 73: | ||
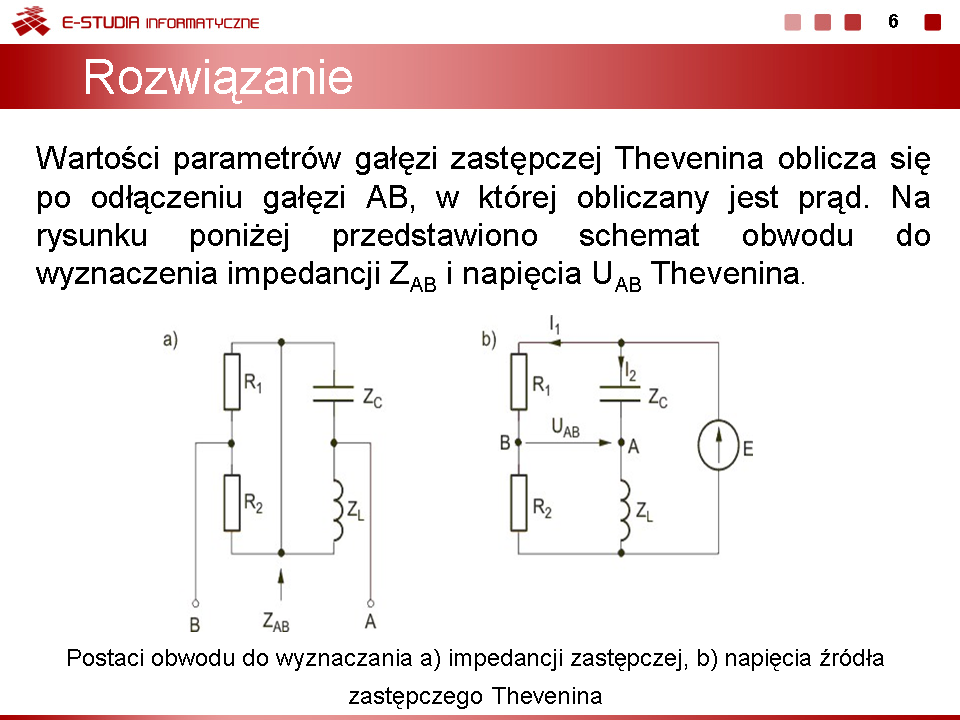
Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego <math>U_{AB}</math> w schemacie zastępczym Thevenina. Obliczając kolejno prądy | Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego <math>U_{AB}</math> w schemacie zastępczym Thevenina. Obliczając kolejno prądy | ||
: <math>I_1={E \over R_1+R_2}=1</math> | : <math>I_1={E \over R_1+R_2}=1</math> | ||
| Linia 79: | Linia 80: | ||
Napięcie <math>U_{AB}</math> określa się ze wzoru | Napięcie <math>U_{AB}</math> określa się ze wzoru | ||
: <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | : <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | ||
| Linia 109: | Linia 111: | ||
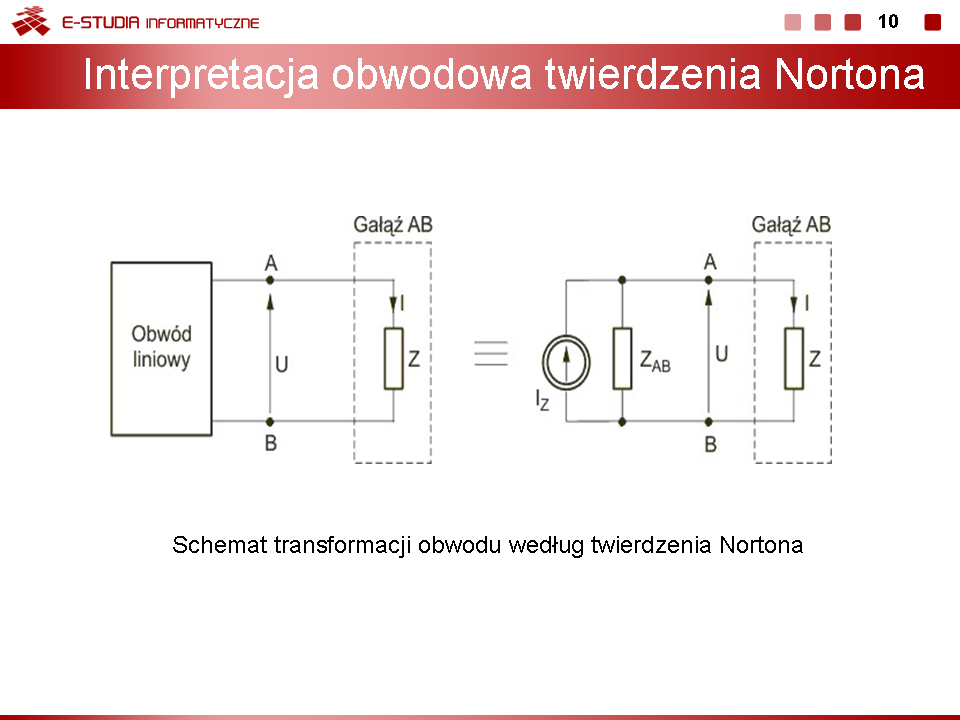
Twierdzenie Nortona pozwala zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem równoległym jednej impedancji zastępczej oraz idealnego źródła prądowego. | Twierdzenie Nortona pozwala zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem równoległym jednej impedancji zastępczej oraz idealnego źródła prądowego. | ||
'''Twierdzenie Nortona''' | |||
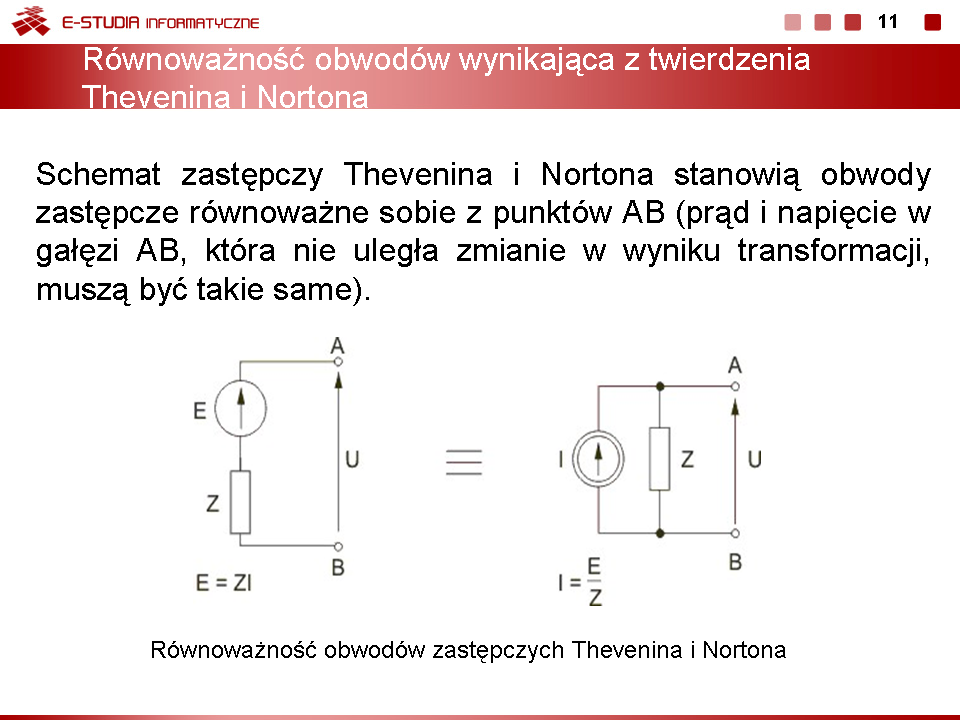
Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | ||
| Linia 156: | Linia 162: | ||
Metoda potencjałów węzłowych, zwana również '''metodą węzłową''', jest jedną z najogólniejszych i najczęściej stosowanych metod, pozwalających wyznaczyć prądy wszystkich gałęzi występujących w obwodzie. Jako zmienne przyjmuje się w niej potencjały poszczególnych węzłów obwodu określane względem jednego arbitralnie wybranego węzła uznanego za '''węzeł odniesienia''' („masy”), którego potencjał przyjmuje się za równy zeru. Liczba równań w tej metodzie jest równa liczbie węzłów niezależnych a więc znacznie mniejsza niż w metodzie wykorzystującej bezpośrednio układ równań otrzymanych w wyniku zastosowania praw Kirchhoffa. | Metoda potencjałów węzłowych, zwana również '''metodą węzłową''', jest jedną z najogólniejszych i najczęściej stosowanych metod, pozwalających wyznaczyć prądy wszystkich gałęzi występujących w obwodzie. Jako zmienne przyjmuje się w niej potencjały poszczególnych węzłów obwodu określane względem jednego arbitralnie wybranego węzła uznanego za '''węzeł odniesienia''' („masy”), którego potencjał przyjmuje się za równy zeru. Liczba równań w tej metodzie jest równa liczbie węzłów niezależnych a więc znacznie mniejsza niż w metodzie wykorzystującej bezpośrednio układ równań otrzymanych w wyniku zastosowania praw Kirchhoffa. | ||
Metoda węzłowa wynika bezpośrednio z równań prądowych Kirchhoffa napisanych dla wszystkich węzłów niezależnych w obwodzie. Prąd każdej gałęzi obwodu jest wyrażany za pośrednictwem potencjałów węzłowych. | Metoda węzłowa wynika bezpośrednio z równań prądowych Kirchhoffa napisanych dla wszystkich węzłów niezależnych w obwodzie. Prąd każdej gałęzi obwodu jest wyrażany za pośrednictwem potencjałów węzłowych. | ||
|} | |} | ||
| Linia 163: | Linia 169: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd13.png]] | ||
|valign="top"|<math>YV=I_{ZR}V=Y^{-1}I_{ZR}</math> | |valign="top"|Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci | ||
<math>YV=I_{ZR}V=Y^{-1}I_{ZR}</math> | |||
w której <math>Y\,</math> jest macierzą węzłową o wymiarach <math>NxN\,</math>, gdzie <math>N\,</math> jest liczbą węzłów niezależnych w obwodzie, <math>V\,</math> jest wektorem niezależnych potencjałów węzłowych o wymiarze <math>N\,</math> a <math>I_{ZR}</math> jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa <math>Y\,</math> określona jest w postaci | w której <math>Y\,</math> jest macierzą węzłową o wymiarach <math>NxN\,</math>, gdzie <math>N\,</math> jest liczbą węzłów niezależnych w obwodzie, <math>V\,</math> jest wektorem niezależnych potencjałów węzłowych o wymiarze <math>N\,</math> a <math>I_{ZR}</math> jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa <math>Y\,</math> określona jest w postaci | ||
| Linia 183: | Linia 192: | ||
V_N | V_N | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
<math>I_{ZR}=\begin{bmatrix} | <math>I_{ZR}=\begin{bmatrix} | ||
| Linia 191: | Linia 199: | ||
I_{ZRN} | I_{ZRN} | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|} | |} | ||
Wersja z 11:33, 24 sie 2006

|
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |

|

|

|
Przykład
Dla obwodu przedstawionego na rysunku napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. |

|
| Zadania sprawdzające
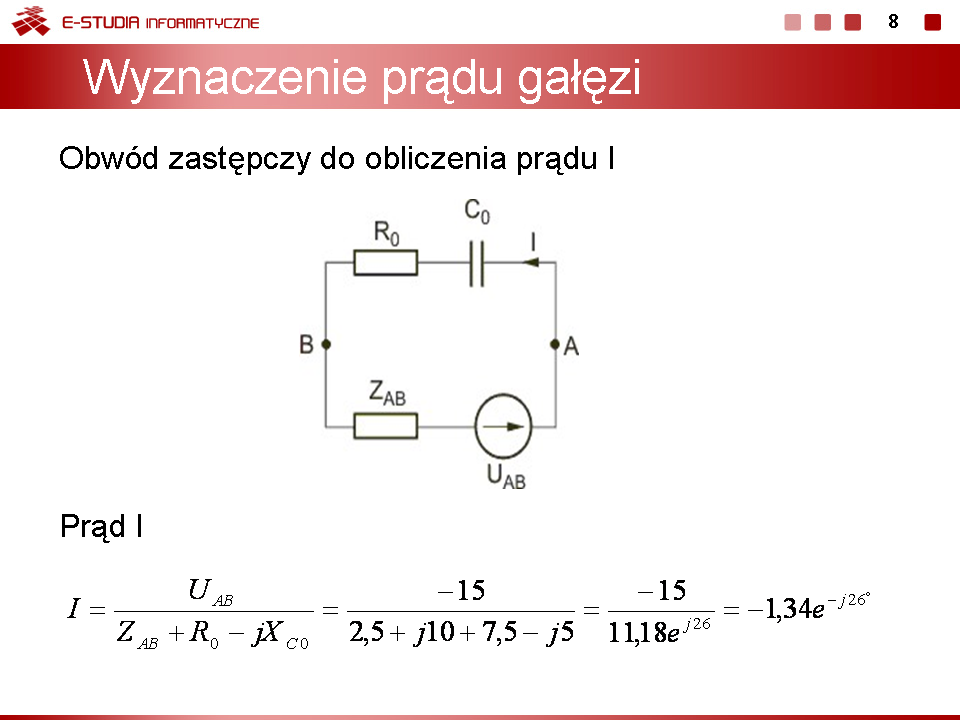
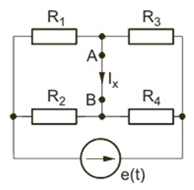
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , . Rozwiązanie Impedancja z zacisków AB obwodu jest równa
Prądy w obwodzie z rys. b:
Napięcie
Poszukiwany prąd z obwodu zastępczego Thevenina (rys. c)
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
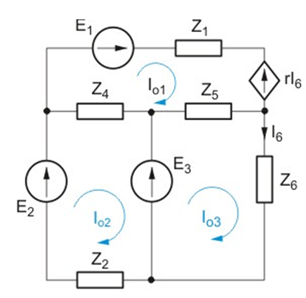
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci |