PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 56: | Linia 56: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png]] | ||
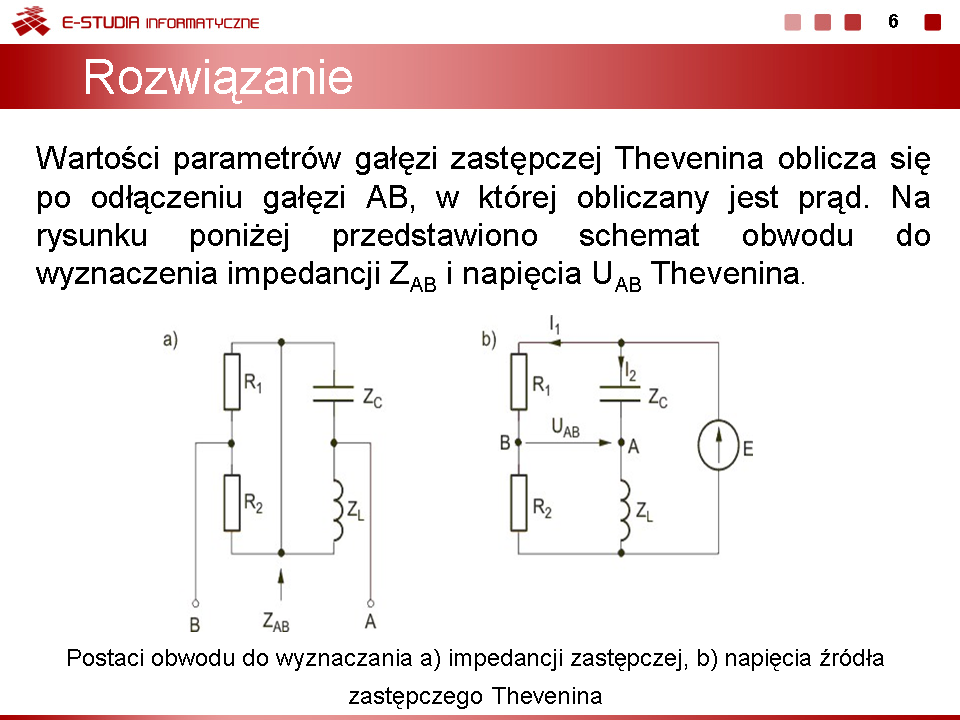
|valign="top"|W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: <math>Z_{AB}</math> i <math>U_{AB}</math>. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. | |valign="top"|W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: <math>Z_{AB}</math> i <math>U_{AB}</math>. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. | ||
Obliczenie impedancji zastępczej <math>Z_{AB}</math> (rysunek a) wymaga wyeliminowania źródeł wymuszających w obwodzie (zwarcie źródła napięciowego). | |||
Obliczenie napięcia <math>U_{AB}</math> (rysuenk b) wymaga jedynie wyeliminowania gałęzi AB bez jakiejkolwiek zmiany w pozostałej części obwodu. | |||
|} | |} | ||
| Linia 63: | Linia 67: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png]] | ||
|valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | |valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | ||
: <math>Z_{AB}={R_1R_2 \over R_1+R_2}+{Z_LZ_C \over Z_L+Z_C}={5 \cdot 5 \over 5+5}+{j5 \cdot (-j10) \over j5-j10}=2,5+j10</math> | : <math>Z_{AB}={R_1R_2 \over R_1+R_2}+{Z_LZ_C \over Z_L+Z_C}={5 \cdot 5 \over 5+5}+{j5 \cdot (-j10) \over j5-j10}=2,5+j10</math> | ||
| Linia 70: | Linia 75: | ||
: <math>I_1={E \over R_1+R_2}=1</math> | : <math>I_1={E \over R_1+R_2}=1</math> | ||
: <math>I_2={E \over jX_L-jX_C}=2j</math> | : <math>I_2={E \over jX_L-jX_C}=2j</math> | ||
Napięcie <math>U_{AB}</math> określa się ze wzoru | |||
: <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | : <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | ||
| Linia 85: | Linia 88: | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png]] | ||
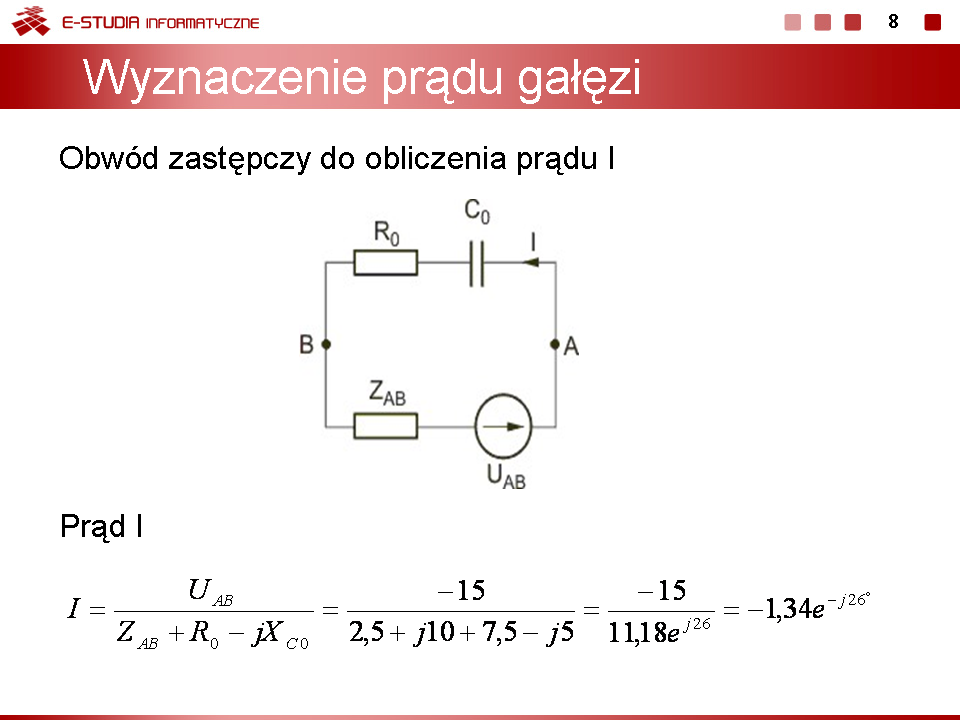
|valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\,</math> określa się ze wzoru | |valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\,</math> określa się ze wzoru | ||
: <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | : <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | ||
Wartości chwilowe prądu <math>i(t)\,</math> wyznaczane są z zależności | Wartości chwilowe prądu <math>i(t)\,</math> wyznaczane są z zależności | ||
: <math>i(t)=-1,34\sqrt{2}sin(\omega t-26^\circ)A</math> | : <math>i(t)=-1,34\sqrt{2}sin(\omega t-26^\circ)A</math> | ||
Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych. | Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych. | ||
|} | |} | ||
| Linia 104: | Linia 106: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd9.png]] | ||
|valign="top"| | |valign="top"|'''Metoda oparta na twierdzeniu Nortona''' | ||
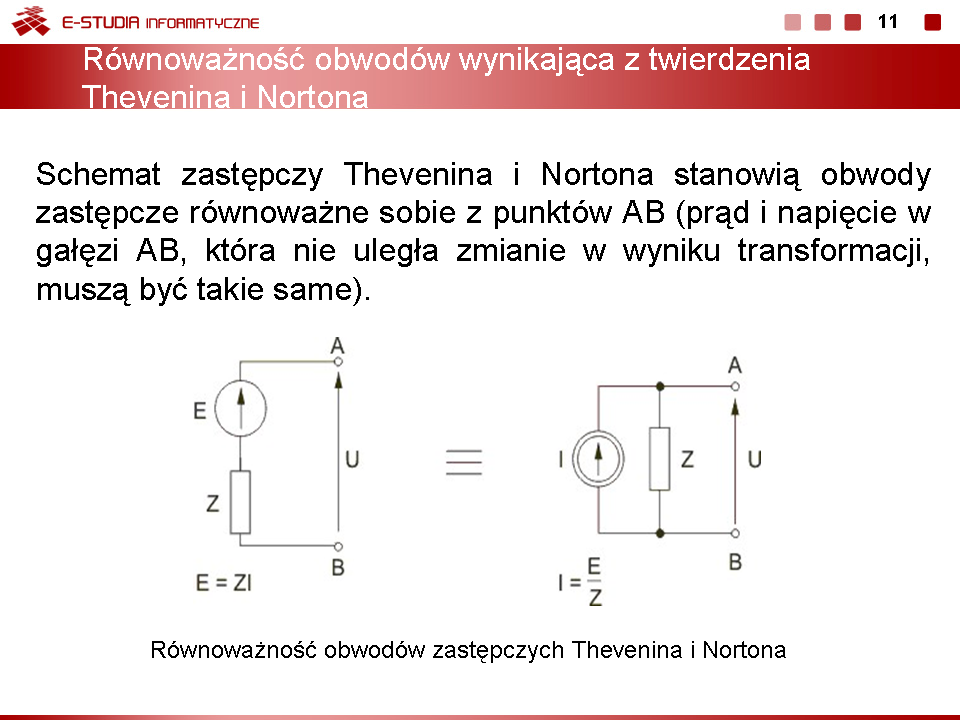
Twierdzenie Nortona pozwala zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem równoległym jednej impedancji zastępczej oraz idealnego źródła prądowego. | |||
Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | ||
|} | |} | ||
| Linia 115: | Linia 118: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd10.png]] | ||
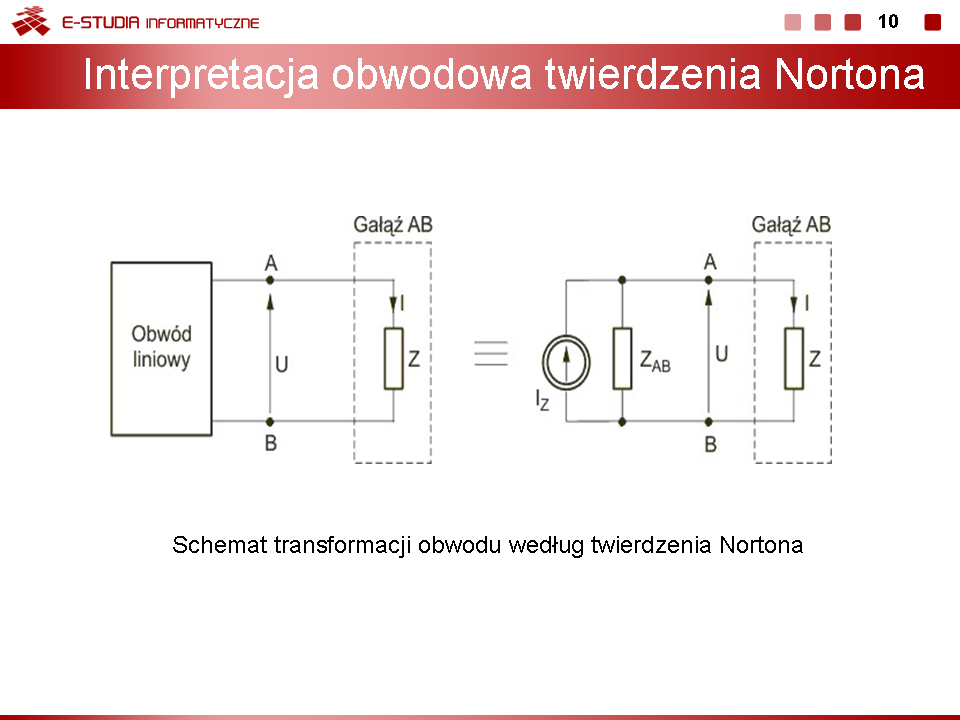
|valign="top"|Prąd <math>I\,</math> oraz napięcie <math>U\,</math> występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi <math>I\,</math> oraz napięciu <math>U\,</math> w tej samej gałęzi obwodu uproszczonego. Źródło prądowe <math>I_Z</math> występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja <math>Z_{AB}</math> jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB reprezentowana jest przez impedancję <math>Z\,</math>, napięcie tej gałęzi oblicza się z prawa prądowego Kirchhoffa <math>I_Z-U({1 \over Z}+{1 \over Z_{AB}})=0</math>, które pozwala wyrazić poszukiwane napięcie gałęzi w postaci | |valign="top"|Rysunek na slajdzie 10 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona. | ||
Prąd <math>I\,</math> oraz napięcie <math>U\,</math> występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi <math>I\,</math> oraz napięciu <math>U\,</math> w tej samej gałęzi obwodu uproszczonego. Źródło prądowe <math>I_Z</math> występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja <math>Z_{AB}</math> jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB reprezentowana jest przez impedancję <math>Z\,</math>, napięcie tej gałęzi oblicza się z prawa prądowego Kirchhoffa <math>I_Z-U({1 \over Z}+{1 \over Z_{AB}})=0</math>, które pozwala wyrazić poszukiwane napięcie gałęzi w postaci | |||
Wersja z 11:30, 24 sie 2006

|
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |

|

|

|
Przykład
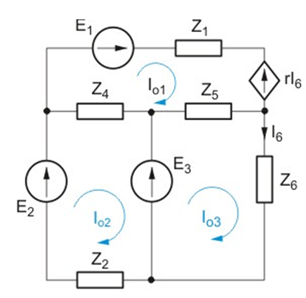
Dla obwodu przedstawionego na rysunku napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. |

|
| Zadania sprawdzające
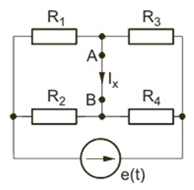
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , . Rozwiązanie Impedancja z zacisków AB obwodu jest równa
Prądy w obwodzie z rys. b:
Napięcie
Poszukiwany prąd z obwodu zastępczego Thevenina (rys. c)
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci |