PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 400: | Linia 400: | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd22.png]] | ||
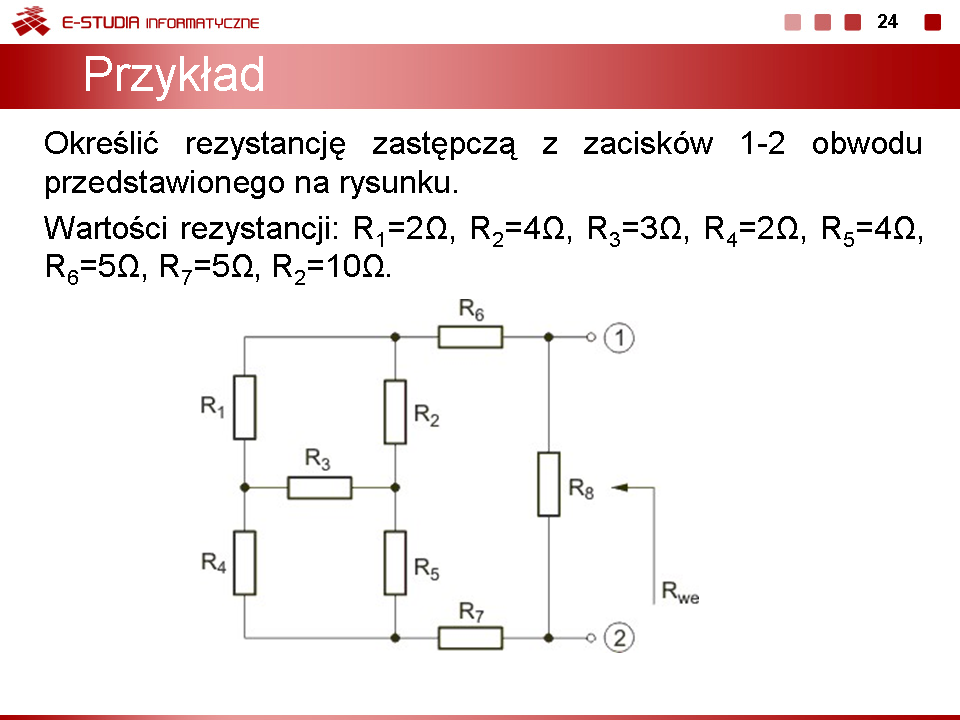
|valign="top"|Jako przykład rozpatrzymy obwód przedstawiony na slajdzie obok, dla którego określimy rezystancję zastępczą z zacisków 1-2. | |valign="top"|Jako przykład rozpatrzymy obwód przedstawiony na slajdzie obok, dla którego określimy rezystancję zastępczą z zacisków 1-2. | ||
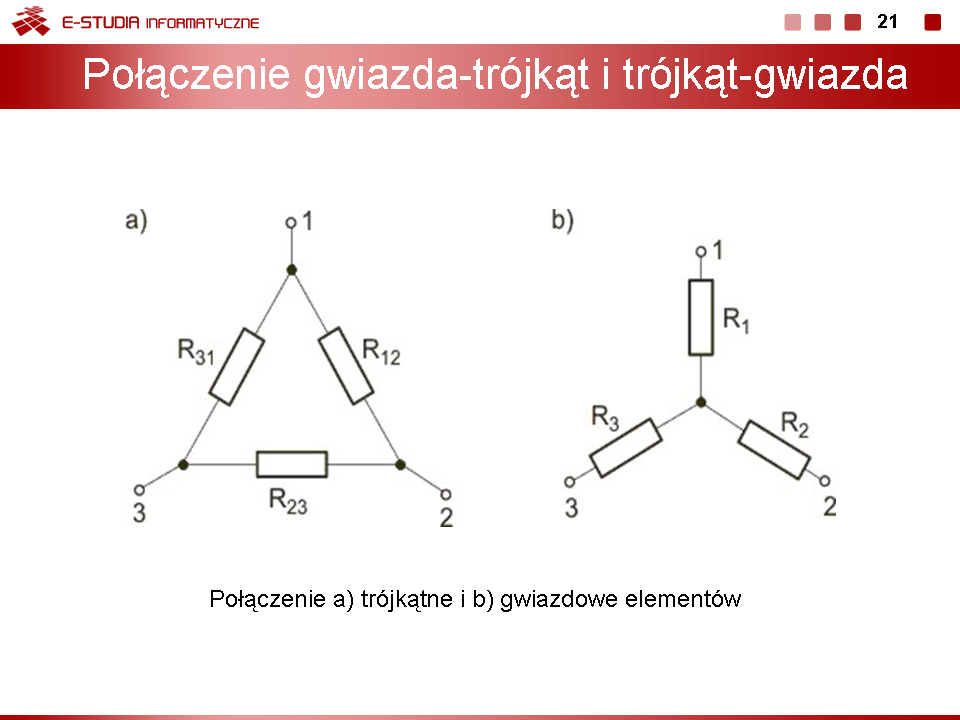
Z punktu widzenia zacisków wejściowych 1-2 w obwodzie nie można wyróżnić żadnego połączenia szeregowego czy równoległego elementów upraszczających obwód. Dla uproszczenia struktury tego obwodu konieczne jest więc zastosowanie przekształcenia gwiazda-trójkąt lub trójkąt-gwiazda w stosunku do rezystorów położonych najdalej od węzłów wejściowych (w wyniku przekształcenia nie mogą ulec likwidacji węzły wejściowe obwodu). | Z punktu widzenia zacisków wejściowych 1-2 w obwodzie nie można wyróżnić żadnego połączenia szeregowego czy równoległego elementów upraszczających obwód. Dla uproszczenia struktury tego obwodu konieczne jest więc zastosowanie przekształcenia gwiazda-trójkąt lub trójkąt-gwiazda w stosunku do rezystorów położonych najdalej od węzłów wejściowych (w wyniku przekształcenia nie mogą ulec likwidacji węzły wejściowe obwodu). | ||
| Linia 414: | Linia 415: | ||
: <math>R_{25}=4+4+{4 \cdot 4 \over3}=13,33</math> | : <math>R_{25}=4+4+{4 \cdot 4 \over3}=13,33</math> | ||
Schemat obwodu po przekształceniach przedstawiony jest na rysunku obok | Schemat obwodu po przekształceniach przedstawiony jest na rysunku obok. | ||
W obwodzie tym można już wyróżnić połączenia równoległe elementów <math>R_1</math> i <math>R_{23}</math> oraz <math>R_4</math> i <math>R_{35}</math>. Wykorzystując regułę upraszczania elementów połączonych równolegle otrzymuje się | W obwodzie tym można już wyróżnić połączenia równoległe elementów <math>R_1</math> i <math>R_{23}</math> oraz <math>R_4</math> i <math>R_{35}</math>. Wykorzystując regułę upraszczania elementów połączonych równolegle otrzymuje się | ||
: <math>R_{ | : <math>R_{z1}={R_1 \cdot R_{23} \over R_1 + R_{23}}=1,667</math> | ||
: <math>R_{ | : <math>R_{z2}={R_4 \cdot R_{35} \over R_4 + R_{35}}=1,667</math> | ||
Rezystory <math>R_{ | Rezystory <math>R_{z1}</math> i <math>R_{z2}</math> są połączone szeregowo. Ich rezystancja zastępcza jest równa | ||
: <math>R_{ | : <math>R_{z3}=R_{z1}+R_{z2}=3,333</math> | ||
Jest ona połączona równolegle z rezystorem <math>R_{25}</math>. Stąd rezystancja zastępcza tego połączenia wynosi | Jest ona połączona równolegle z rezystorem <math>R_{25}</math>. Stąd rezystancja zastępcza tego połączenia wynosi | ||
: <math>R_{ | : <math>R_{z4}={3,333 \cdot 13,333 \over 3,333+13,333}=2,667</math> | ||
Rezystory <math>R_6</math>, <math>R_{ | Rezystory <math>R_6</math>, <math>R_{z4}</math> i <math>R_7</math> są połączone szeregowo. Ich rezystancja zastępcza wynosi więc: | ||
: <math>R_{ | : <math>R_{z5}=R_6+R_{z4}+R_7=12,667</math> | ||
Rezystancja ta jest z kolei połączona równolegle z rezystancją <math>R_8</math> tworząc wypadkową rezystancję obwodu widzianą z zacisków zewnętrznych. Stąd całkowita rezystancja zastępcza obwodu wyraża się wzorem | Rezystancja ta jest z kolei połączona równolegle z rezystancją <math>R_8</math> tworząc wypadkową rezystancję obwodu widzianą z zacisków zewnętrznych. Stąd całkowita rezystancja zastępcza obwodu wyraża się wzorem | ||
: <math>R_{we}={{R_{ | : <math>R_{we}={{R_{z5}R_8} \over {R_{z5}+R_8}}={{12,667 \cdot 10} \over {12,667+10}}=5,588 \Ohm</math> | ||
|} | |} | ||
Wersja z 08:02, 24 sie 2006

|

|
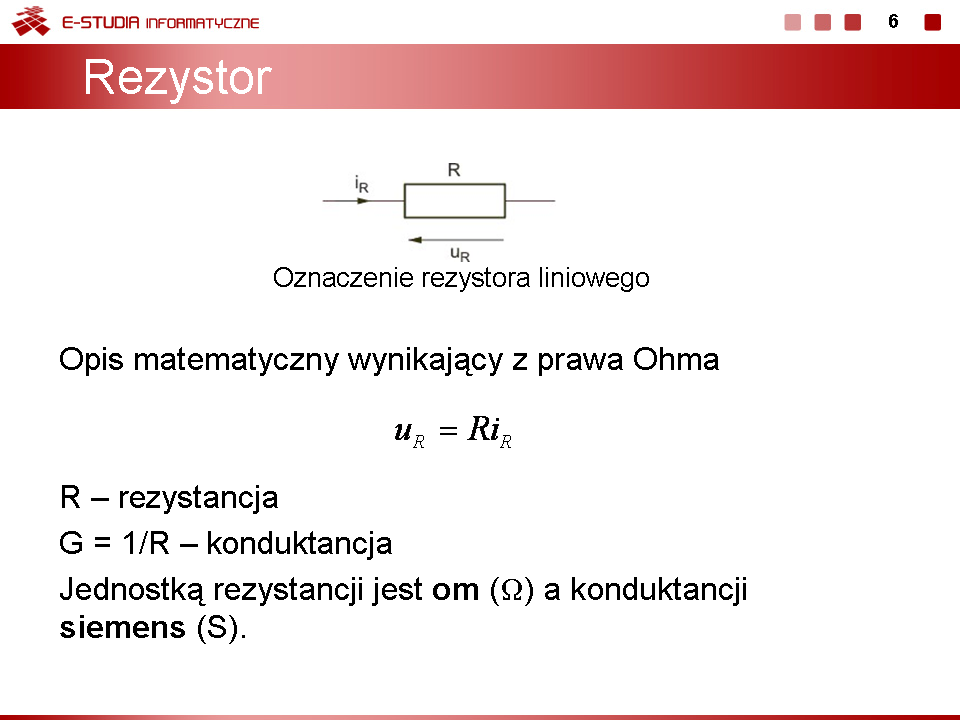
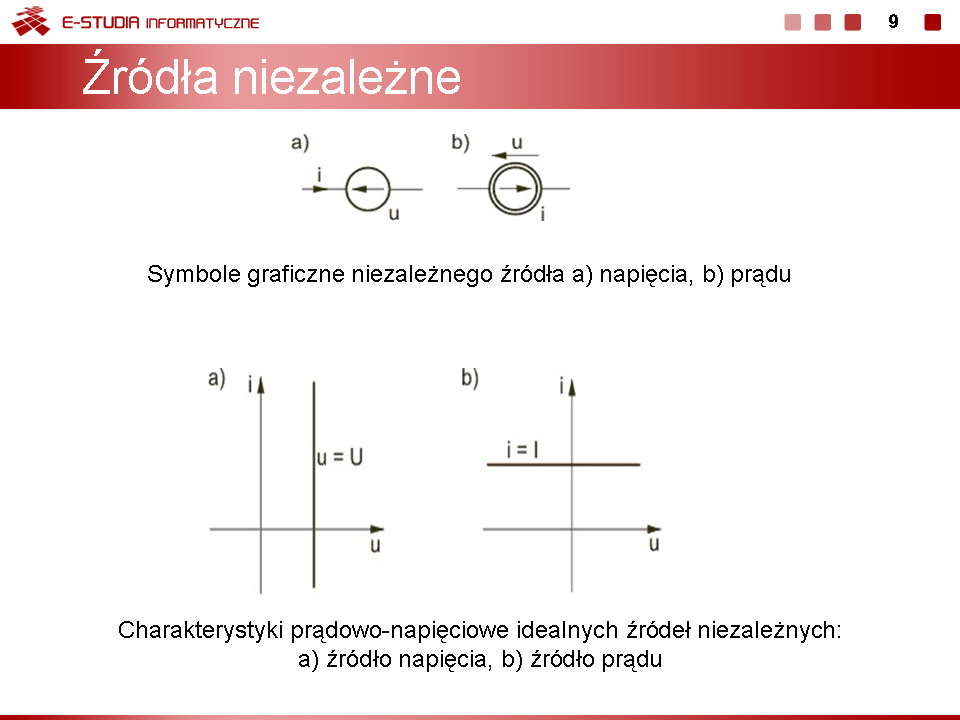
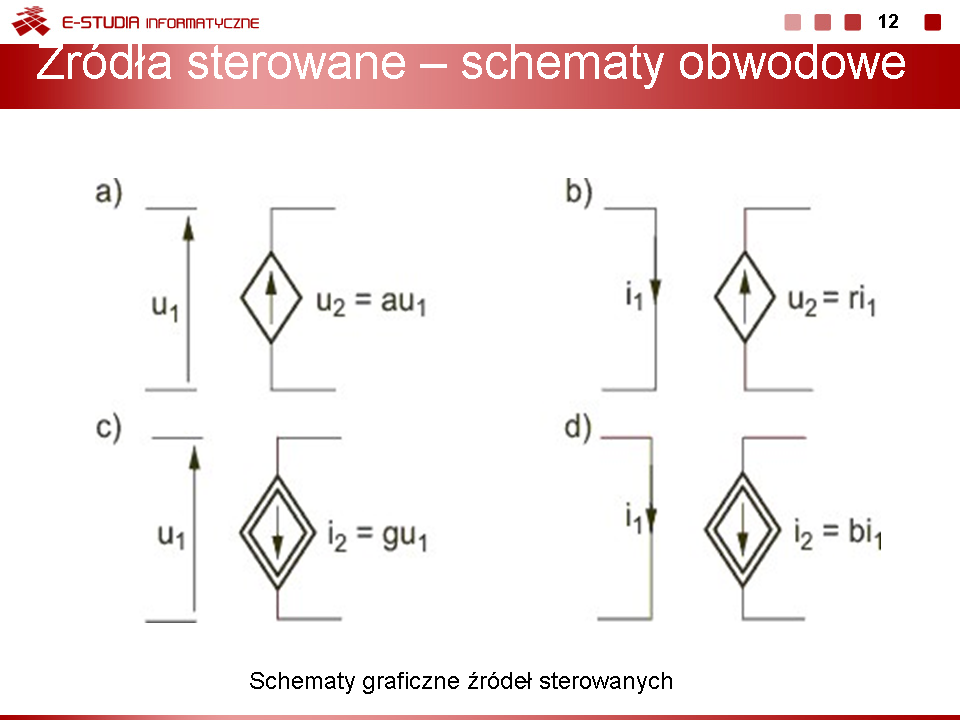
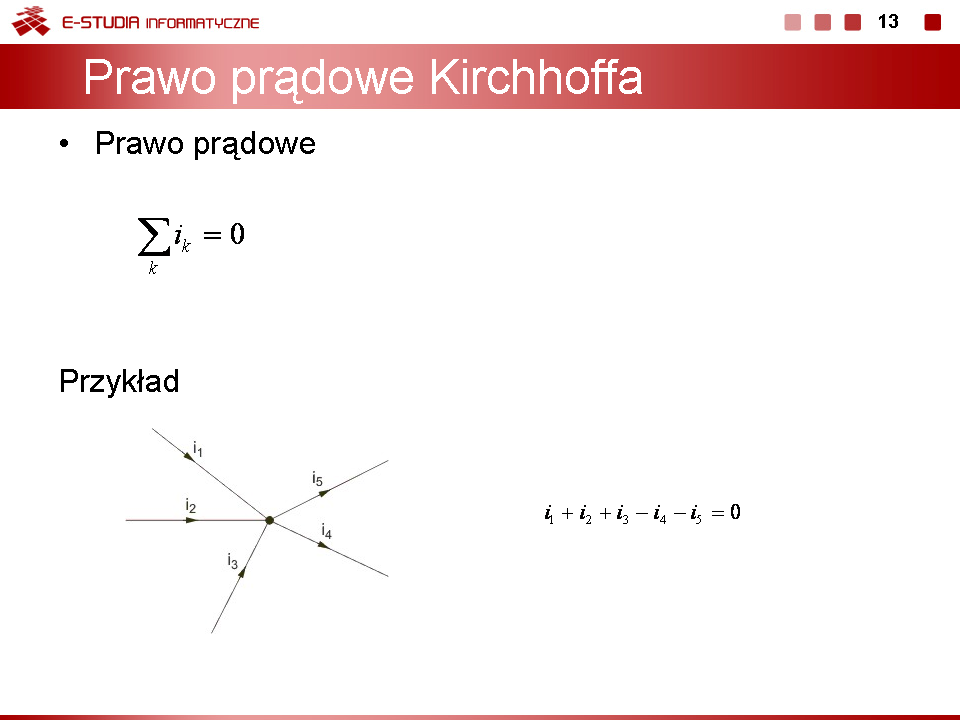
Wykład 1 Podstawowe prawa obwodów elektrycznych |
| Zadania sprawdzające
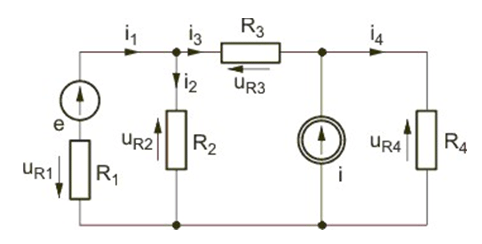
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
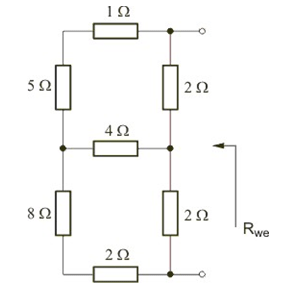
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |