PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 167: | Linia 167: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd12.png]] | ||
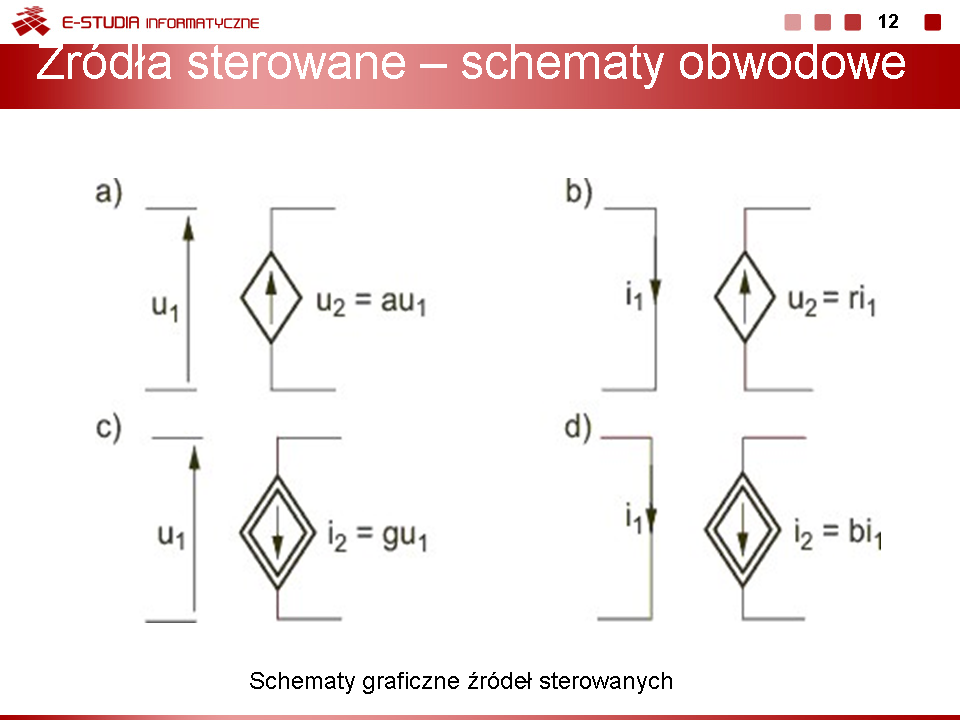
|valign="top"|Schematy graficzne wszystkich wymienionych tu rodzajów źródeł sterowanych prądu i napięcia przedstawione są na rysunku | |valign="top"|Schematy graficzne wszystkich wymienionych tu rodzajów źródeł sterowanych prądu i napięcia przedstawione są na rysunku (slajd obok). | ||
Wielkości <math>r\,</math>, <math>g\,</math> oraz <math>a\,</math> i <math>b\,</math> stanowią współczynniki proporcjonalności między wielkością sterująca i sterowaną tych źródeł. Przyjmują one najczęściej wartości rzeczywiste, choć w różnego rodzaju modelach mogą być również opisane funkcją zespoloną. Należy nadmienić, że źródła sterowane stanowią bardzo popularne modele wielu elementów elektrycznych i elektronicznych, takich jak transformatory idealne, maszyny elektryczne, tranzystory bipolarne i polowe, wzmacniacze operacyjne napięciowe i prądowe, itp. | Wielkości <math>r\,</math>, <math>g\,</math> oraz <math>a\,</math> i <math>b\,</math> stanowią współczynniki proporcjonalności między wielkością sterująca i sterowaną tych źródeł. Przyjmują one najczęściej wartości rzeczywiste, choć w różnego rodzaju modelach mogą być również opisane funkcją zespoloną. Należy nadmienić, że źródła sterowane stanowią bardzo popularne modele wielu elementów elektrycznych i elektronicznych, takich jak transformatory idealne, maszyny elektryczne, tranzystory bipolarne i polowe, wzmacniacze operacyjne napięciowe i prądowe, itp. | ||
|} | |} | ||
| Linia 231: | Linia 231: | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd13.png]] | |||
|valign="top"|'''Prawa Kirchhoffa''' | |||
Pod pojęciem analizy obwodu elektrycznego rozumie się proces określania rozpływu prądów i rozkładu napięć w obwodzie przy założeniu, że znana jest struktura obwodu oraz wartości wszystkich jego elementów. Podstawę analizy obwodów elektrycznych stanowią prawa Kirchhoffa, podane przez niemieckiego fizyka Gustawa Kirchhoffa w dziewiętnastym wieku. Wyróżnia się dwa prawa określające rozpływ prądów i rozkład napięć w obwodzie. Pierwsze prawo Kirchhoffa kojarzy się zwykle z bilansem prądów w węźle obwodu elektrycznego a drugie z bilansem napięć w oczku. | |||
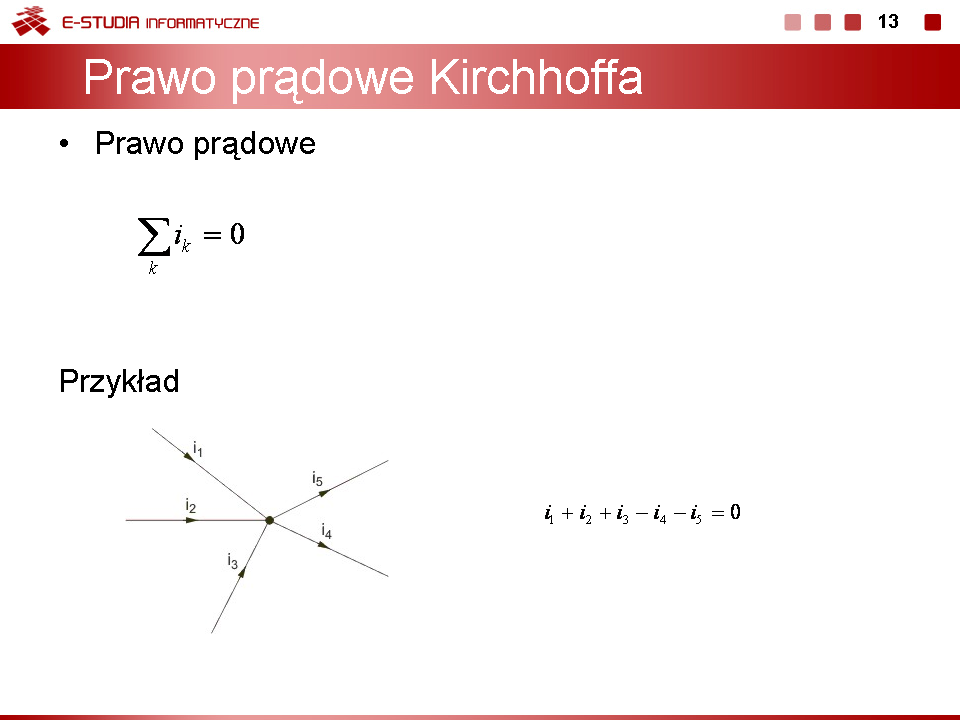
'''Prawo prądowe Kirchhoffa''' | |||
Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru | |||
<math>\sum_{k}=i_k=0\,</math> | |||
Sumowanie dotyczy wszystkich prądów, które dopływają lub odpływają z danego oczka, przy czym wszystkie prądy wpływające do węzła brane są z jednakowym znakiem a wszystkie prądy wypływające z węzła ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów wpływających czy wypływających). Sposób tworzenia równania prądowego Kirchhoffa zilustrujemy dla jednego węzła obwodu przedstawionego na rysunku obok. | |||
Prawo Kirchhoffa dla tego węzła z uwzględnieniem kierunków prądów w węźle zapiszemy w postaci: | |||
<math>i_1+i_2+i_3-i_4-i_5=0</math> | |||
Można je również zapisać jako bilans prądów dopływających i odpływających od węzła w postaci: | |||
<math>i_1+i_2+i_3=i_4+i_5</math> | |||
Dla każdego obwodu można napisać dokładnie <math>n-1\,</math> niezależnych równań prądowych, gdzie <math>n\,</math> oznacza całkowitą liczbę węzłów a <math>(n-1)</math> liczbę węzłów niezależnych. Bilans prądów w pozostałym <math>n\,</math>-tym węźle obwodu wynika z równań prądowych napisanych dla <math>n-1\,</math> węzłów (jest to węzeł zależny zwany węzłem odniesienia). Wybór węzła odniesienia jest całkowicie dowolny. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd13.png]] | |||
|valign="top"|'''Prawa Kirchhoffa''' | |||
'''Prawo napięciowe Kirchhoffa''' | |||
Suma napięć w każdym oczku obwodu elektrycznego jest równa zeru | |||
<math>\sum_k=u_k=0</math> | |||
Sumowanie dotyczy napięć gałęziowych występujących w danym oczku zorientowanych względem dowolnie przyjętego kierunku odniesienia. Napięcie gałęziowe zgodne z tym kierunkiem jest brane z plusem a przeciwne z minusem. Sposób pisania równań wynikających z prawa napięciowego Kirchhoffa pokażemy na przykładzie oczka obwodu przedstawionego na rysunku obok. | |||
Uwzględniając kierunki napięć gałęziowych równanie napięciowe Kirchhoffa dla tego oczka przyjmie postać: | |||
<math>u_1+u_2+u_3-u_4-e=0</math> | |||
Można je również zapisać jako bilans napięć źródłowych i odbiornikowych w postaci: | |||
<math>e=u_1+u_2+u_3-u_4</math> | |||
Dla każdego obwodu można napisać tyle równań oczkowych ile oczek wyodrębnimy w tym obwodzie, przy czym część równań oczkowych będzie równaniami zależnymi (wynikającymi z liniowej kombinacji innych równań). Liczba równań oczkowych branych pod uwagę w analizie jest więc równa liczbie oczek niezależnych. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
Wersja z 07:34, 24 sie 2006

|

|
Wykład 1 Podstawowe prawa obwodów elektrycznych |

|
|
| Zadania sprawdzające
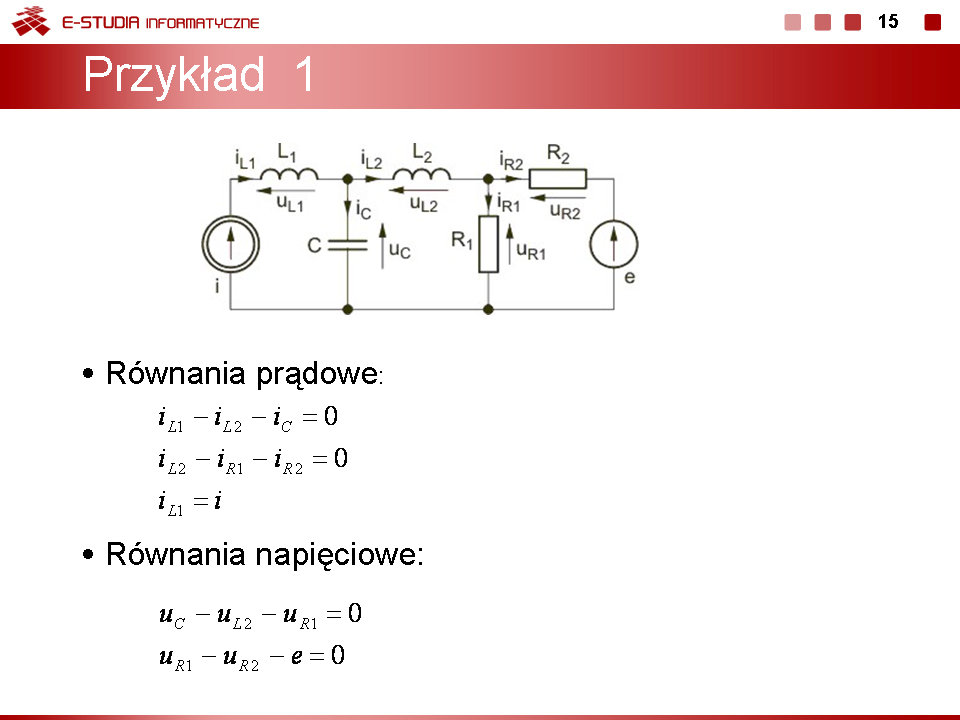
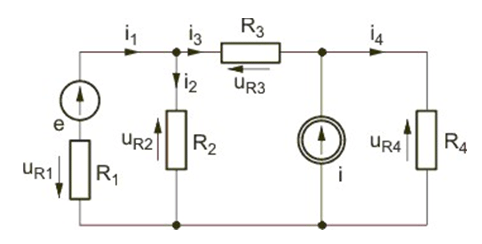
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
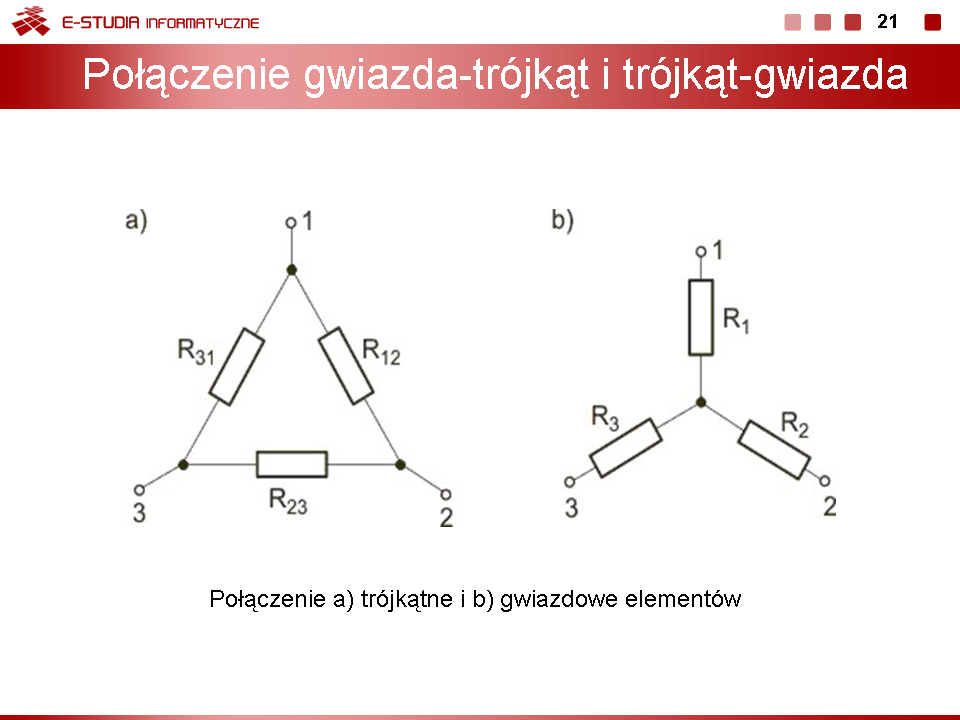
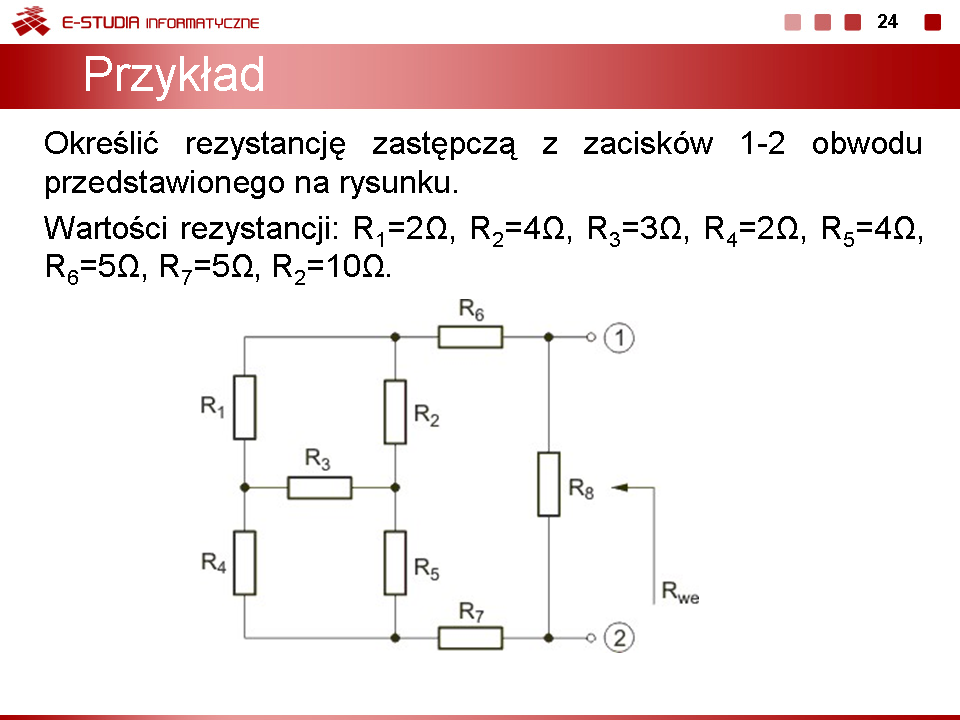
Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |