TTS Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 229: | Linia 229: | ||
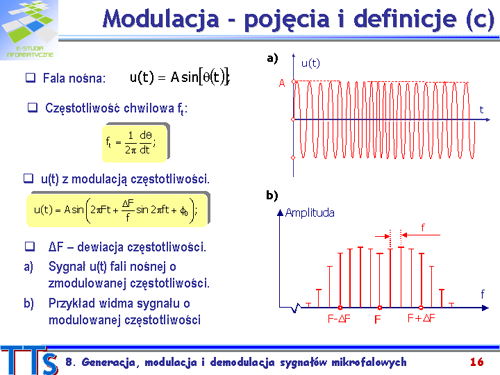
Na rysunku a) pokazano przykład przebiegu <math>u(t)\,</math> zgodnej z powyższą zależnością. Po rozwinięciu zależności na <math>u(t)\,</math> w szereg Fouriera otrzymuje się nieskończenie wiele składowych, wstęg bocznych wokół częstotliwości <math>F\,</math> fali nośnej. Amplituda n-tej wstęgi bocznej jest proporcjonalna do <math>AJ_n(\Delta F/f)\,</math>. Pojawia się tutaj funkcja Bessela n-tego rzędu, od parametru <math>\Delta F/f\,</math>. Rzut oka na wykresy rodziny funkcji Bessela pozwala wyciągnąć wniosek, że amplitudy kolejnych składowych szybko maleją ze wzrostem <math>n\,</math> . | Na rysunku a) pokazano przykład przebiegu <math>u(t)\,</math> zgodnej z powyższą zależnością. Po rozwinięciu zależności na <math>u(t)\,</math> w szereg Fouriera otrzymuje się nieskończenie wiele składowych, wstęg bocznych wokół częstotliwości <math>F\,</math> fali nośnej. Amplituda n-tej wstęgi bocznej jest proporcjonalna do <math>AJ_n(\Delta F/f)\,</math>. Pojawia się tutaj funkcja Bessela n-tego rzędu, od parametru <math>\Delta F/f\,</math>. Rzut oka na wykresy rodziny funkcji Bessela pozwala wyciągnąć wniosek, że amplitudy kolejnych składowych szybko maleją ze wzrostem <math>n\,</math> . | ||
W niektórych przypadkach stosowana jest modulacja fazy. | |||
Porównując modelację częstotliwości z modulacją fazy zauważamy, że: | |||
*Dla modulacji PM - dewiacja częstotliwości proporcjonalna do <math>f\,</math>. | |||
*Dla modulacji FM dewiacja częstotliwości niezależna od <math>f\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M8_Slajd17.png]] | |||
|valign="top"|Przy transmisji sygnałów cyfrowych stosujemy '''modulację impulsową''', zwaną też inaczej '''modulacją cyfrową'''. Sygnał cyfrowy ma rozmaitą formę. Sygnały transmitowane w systemach komputerowych mają kształt pokazany na rysunku nazywane są binarnymi. | |||
Do transmisji sygnałów cyfrowych można wykorzystać każdy z opisanych wyżej rodzajów modulacji: amplitudy, częstotliwości i fazy. Wykorzystując modulację amplitudy nadajemy amplitudzie fali nośnej dwie wartości: dużą i małą (np. 0) – rys.9.5b. Dla cyfrowej modulacji częstotliwości częstotliwość fali nośnej przyjmuje dwie różne wartości dla ”1” i dla ”0” – patrz rysunek. W przypadku cyfrowej modulacji fazy faza sygnału fali nośnej przyjmuje dwie różne wartości dla ”1” i dla ”0”. | |||
W wielu przypadkach, np. telefonii komórkowej, stosujemy modulację cyfrową wielostanową. | |||
Modulację amplitudy AM i fazy PM uzyskuje się transmitując sygnał fali nośnej przez dwuwrotnik o kontrolowanych elektrycznie parametrach. Zwykle jest to transmitancja <math>S_{21}\,</math>. | |||
*Chcąc uzyskać modulację amplitudy dwuwrotnik konstruowany jest w taki sposób, aby moduł transmitancji <math>|S_{21}[U(t)]|\,</math> zmieniał się w takt napięcia fali modulującej. | |||
*W przypadku modulacji fazy PM napięcie fali modulującej zmienia fazę <math>\phi [U(t)]\,</math> transmitancji dwuwrotnika. | |||
Modulację częstotliwości FM uzyskuje się przez bezpośrednią ingerencję w warunek generacji oscylatora, przez zmianę częstotliwości generacji, najczęściej przez doprowadzenie napięcia do diody waraktorowej kontrolującej częstotliwość oscylatora tranzystorowego. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M8_Slajd18.png]] | |||
|valign="top"|Obecność w obwodzie elementu nieliniowego, dla którego prąd i napięcie nie są związane prawem Ohma, jest źródłem wielu efektów. Rozważmy najprostszy obwód z rysunku, w którym źródło napięciowe <math>V\,</math> połączono z nieliniowym rezystorem <math>R\,</math>. | |||
Zachowanie się rezystora <math>R\,</math> opiszemy szeregiem potęgowym. Przyjmiemy dalej, że napięcie <math>V\,</math>źródła napięciowego jest sumą dwóch sinusoidalnie zmiennych składników o częstotliwościach <math>f_H\,</math> i <math>f_S\,</math>. W prądzie i pojawia się wiele składników przemiany o częstotliwościach wyrażonych podaną zależnością. | |||
Rozmaite składniki można wykorzystać do rozmaitych celów. Aby to zrobić musimy znaleźć elementy nieliniowe, o znanych właściwościach i modelach, łatwo wytwarzanych i dających się zastosować w obwodach mikrofalowych. Takimi elementami są diody Schottky;ego i tranzystory mikrofalowe. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M8_Slajd19.png]] | |||
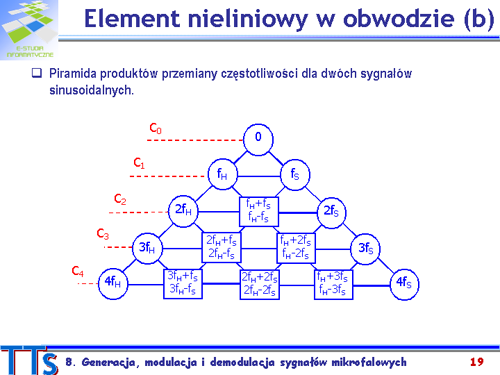
|valign="top"|Na rysunku pokazano piramidę produktów przemiany częstotliwości dla dwóch sygnałów sinusoidalnych, wskazującą kolejne produkty wyrazów szeregu. | |||
Przypatrzmy się składnikom prądu w obwodzie i roli poszczególnych wyrazów szeregu. | |||
*Wyraz pierwszy <math>C_0\,</math> reprezentuje składową stałą, składowa ta zostania powiększona. | |||
*Wyraz drugi z <math>C_1\,</math> ma wymiar konduktancji, to składnik liniowy. | |||
*Wyraz trzeci z <math>C_2\,</math> dostarcza składników: <math>2\omega_H,\,</math> <math>2\omega_S\,</math> , <math>(\omega_H+\omega_S)\</math> , <math>(\omega_H-\omega_S)\,</math> oraz powoduje przyrost składowej stałej. | |||
*Wyraz czwarty z <math>C_3\,</math> także powoduje przyrost składowej stałej oraz dostarcza dużą grupę składników: <math>\omega_H\,</math> , <math>3\omega_H\,</math> , <math>\omega_S\,</math> , <math>3\omega_S\,</math> , <math>(2\omega_H+\omega_S)\,</math> , <math>(2\omega_H-\omega_S)\,</math> , <math>(\omega_H+2\omega_S)\,</math> , <math>(\omega_H-2\omega_S)\,</math> | |||
Wersja z 15:57, 23 sie 2006

|
Materiał obu części Wykładu jest obszerny i zapoznaje on studiującego z wieloma nowymi zagadnieniami, technikami i z wielką liczbą nowych pojęć. |