PF Moduł 8

Wprowadzenie Omówione są tu ogólne prawa makroskopowe opisujące prawidłowo zjawiska cieplne i pozwalające ilościowo przewidywać skutki różnych procesów.

---

Oznaczamy przez $\mathrm{\Delta }U$ zmianę energii wewnętrznej układu, który przechodzi ze stanu o energii wewnętrznej $U_1$ do stanu o energii wewnętrznej $U_2$. Zmiana ta może zachodzić na kilka sposobów: przez wykonanie pracy W nad układem lub przez układ nad otoczeniem, przez wymianę ciepła Q między układem i otoczeniem, przez wymianę materii M pomiędzy układem, a otoczeniem. Zapiszemy to następująco $\mathrm{\Delta }U=U_2-U_1=W+Q+M$ Wzór ten wyraża zasadę zachowania energii w procesach termodynamicznych i nosi nazwę pierwszej zasady termodynamiki. Zasada ta może, być sformułowana w następujący sposób: Przyrost energii wewnętrznej układu przy przejściu ze stanu początkowego do końcowego równy jest sumie dostarczonej do układu energii cieplnej, wykonanej nad układem pracy oraz energii uzyskanej wskutek wymiany materii z otoczeniem. Przyrost ten nie zależy od sposobu, w jaki dokonuje się przejście, a określony jest całkowicie przez początkowy i końcowy stan układu. Niemożliwe jest skonstruowanie silnika cyklicznego, który pracowałby bez pobierania z otoczenia energii. Taki hipotetyczny silnik nazwano perpetuum mobile I-go rodzaju. Niekiedy formułuje się pierwszą zasadę termodynamiki jako niemożliwość skonstruowania perpetuum mobile pierwszego rodzaju to jest skonstruowanie silnika cyklicznego, który pracowałby bez pobierania z otoczenia energii. Zaczerpnięty z łaciny zwrot "perpetuum mobile" znaczy "wiecznie poruszający się".

---

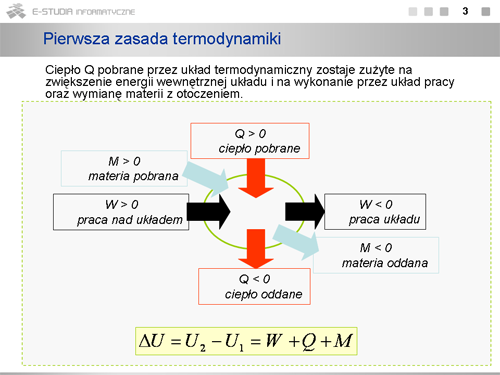
W ten sposób pierwsza zasada termodynamiki wskazuje na trzy różne sposoby zmiany energii wewnętrznej układu: na drodze wykonywania pracy nad układem bądź przez układ oraz poprzez wymianę ciepła lub/i materii pomiędzy układem a otoczeniem.

---

W naszych dalszych rozważaniach będziemy omawiać układy nie wymieniające materii z otoczeniem, dla których M=0. Zmiana energii wewnętrznej $\mathrm{\Delta }U$ układu o stałej masie dokonuje się poprzez wymianę ciepła $Q$, co zachodzi w warunkach różnicy temperatur pomiędzy układem i otoczeniem, lub/i poprzez pracę $W$ wykonaną nad układem lub przez układ nad otoczeniem. $\mathrm{\Delta }Q=Q+W$. Wprowadzamy tu konwencję, którą będziemy stosować w dalszych rozważaniach dla układów nie wymieniających materii z otoczeniem. Praca $W$ jest dodatnia $(W>0)$, jeżeli jest wykonywana przez siły zewnętrzne (otoczenie) nad układem fizycznym. Kiedy układ fizyczny wykonuje pracę nad otoczeniem (kosztem swej energii wewnętrznej) praca ta jest ujemna $(W<0)$. Podobnie, ciepło jest dodatnie $(Q>0)$, jeśli przepływa z otoczenia do układu, a ujemne $(Q<0)$, jeśli przepływa z układu do otoczenia. Dla przykładu, kiedy siły zewnętrzne (otoczenie) wykonują pracę sprężając gaz $(\mathrm{\Delta }V<0)$, to wykonana praca jest dodatnia, kiedy gaz wykonuje pracę nad otoczeniem rozprężając się $(\mathrm{\Delta }V>0)$, praca jest ujemna.

---

Dla wyznaczenia skończonej pracy wykonanej w procesie kwazistatycznym, odwracalnym, można rozpatrywać przemianę jako ciąg procesów elementarnych, w których zmiany parametrów układu są nieskończenie małe. Dla procesu elementarnego zapiszemy pierwsza zasadę termodynamiki w postaci $dU=\delta Q+\delta W$ UWAGA: Symbolami $\delta Q$ i $\delta W$ oznaczamy różniczkowe porcje (a nie skończone przyrosty) wymienianego przez układ ciepła i wykonanej pracy przy nieskończenie małych (infinitezymalnych) zmianach parametrów stanu układu. Wynika, to z faktu, ze ciepło i praca nie są funkcjami stanu, bowiem jak zobaczymy, zależą od drogi przejścia pomiędzy stanami. Mówimy, że są funkcjami procesu. Symbol $dU$ oznacza zmianę energii wewnętrznej, która jest funkcją stanu. W przemianie kołowej, kiedy układ powraca do stanu początkowego, jego energia wewnętrzna mieć będzie taką samą wartość jak w stanie początkowym, co zapisujemy w postaci $\oint dU=0$ Nieskończenie mały przyrost, dla którego spełniony jest powyższy warunek nazywamy różniczką zupełną. Kiedy warunek ten nie jest spełniony, mamy do czynienia z wyrażeniem różniczkowym. Różniczkami zupełnymi są nieskończenie małe przyrosty funkcji stanu, ale nie są nimi infinitezymalne ilości wymienianego ciepła, lub wykonanej pracy. Bilans ilości ciepła pobranego i oddanego przez układ w przemianie kołowej lub wykonanej przez układ pracy nie musi być równy zeru.

---

Przemiana izochoryczna to proces, w którym objętość układu pozostaje stała, czyli $V=const$. W przemianie tej nie jest wykonywana praca. W oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację $\delta Q_v=du$, co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła. Pojemność cieplna jednego mola, tzw. ciepło molowe substancji w procesie przebiegającym bez zmiany objętości wyraża się wzorem $C_v=(\frac{\partial U}{\partial T}{)}_v$, gdzie indeks v przy znaku pochodnej cząstkowej oznacza, że proces zachodzi w stałej objętości. Energia wewnętrzna danej masy gazu doskonałego zależy jednak wyłącznie od temperatury. Przekonuje nas o tym doświadczenie J.P. Joule'a z rozprężaniem rozrzedzonego gazu do próżni, gdy układ jest w osłonie izolacyjnej uniemożliwiającej wymianę ciepła z otoczeniem. Możemy wiec dla gazu doskonałego napisać, że $C_v=\frac{dU}{dT}$. W dowolnym procesie kwazistatycznym, odwracalnym, niezależnie, która z wielkości jest stała zmiana energii wewnętrznej $n_M$ moli gazu doskonałego jest określona wzorem: $dU=n_M\cdot C_v\cdot dT$. Bardziej szczegółowe uzasadnienie tego wzoru, w oparciu o analizę doświadczenia Joule'a, można znaleźć w literaturze. Zapamiętajmy, że powyższy wzór, określający zmianę energii wewnętrznej, ma charakter uniwersalny. Mimo że został sformułowany dla przypadku przemiany izochorycznej i występuje w nim ciepło molowe $C_v$, może być stosowany przy opisie innych przemian gazowych, gdyż energia wewnętrzna jest funkcją stanu. Informacja ta jest bardzo użyteczna przy rozwiązywaniu zadań.

---

---

---

---