SW wykład 3 - Slajd5

<<powrót do strony wykładu

Semantyka naturalna Semantyka naturalna Tiny Sens definicji Sens definicji, c.d. Dowody Indukcja po strukturze Własności Równoważność semantyczna Kongruencje Semantyka operacyjna a naturalna Semantyka operacyjna a naturalna, c.d. Semantyka operacyjna a naturalna, c.d. Semantyka "denotacyjna" Semantyka operacyjna a naturalna, c.d. Równoważność operacyjna Niedeterminizm Kilka równoważności Równoległość

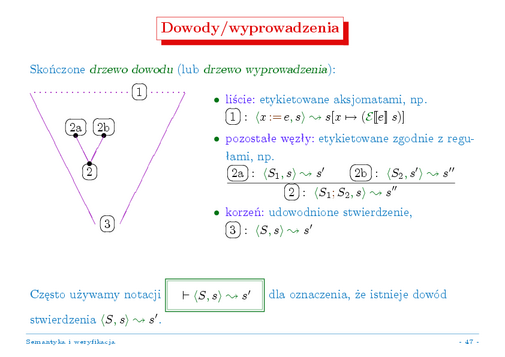
Oczywiście, nie będziemy tu powtarzać wykładu o teorii dowodzenia --- po pełniejszą prezentację tej tematyki można sięgnąć do zajęć "Logika i teoria mnogości", a jeszcze lepiej do bardziej zaawansowanych zajęć "Logika dla informatyków".

Potwierdźmy więc tylko oczekiwane intuicje: wyprowadzenie (dowód) w takim systemie dowodzenia można prezentować jako (skończone) drzewo, którego liście są etykietowane aksjomatami systemu (dokładniej: ich instancjami), a kolejne węzły odpowiadają aplikacji w dowodzie reguł dowodzenia (dokładniej znów: ich instancji), to znaczy bezpośredni potomkowie danego węzła muszą nosić etykiety odpowiadające przesłankom reguły, a sam węzeł -- jej konkluzji. Oczywiście, muszą też by.c spełnione wszelkie warunki dodatkowe stosowalności reguły. Wówczas korzeń tak zbudowanego drzewa dowodu etykietowany jest udowodnionym stwierdzeniem.

Łatwo już teraz pokazać, że dany system reguł semantyki naturalnej definiuje tę samą relację przejścia od konfiguracji do odpowiadających im stanów końcowych przy rozumieniu "teoriomnogościowym" i przy rozumienie "dowodowym". Po pierwsze, zauważmy bowiem, że relacja przejścia wyznaczona przez rozumienie "dowodowe" spełnia implikacje zapisane jako reguły dowodzenia, a zatem zawiera relację wyznaczoną przez rozumienie "teoriomnogościowe", jako najmniejszą relację spełniającą te implikacje. Po drugie zaś, można pokazać, że każda relacja przejścia spełniająca te implikacje zawiera relację wyznaczoną przez rozumienie "dowodowe".